湘教版初中数学九年级下册2.5.2圆的切线 同步练习
试卷更新日期:2021-12-23 类型:同步测试
一、单选题
-
1. 如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( )
 A、65° B、130° C、50° D、100°2. 如图,在平面直角坐标系中,过边长为1的正方形格点A、B、C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A、65° B、130° C、50° D、100°2. 如图,在平面直角坐标系中,过边长为1的正方形格点A、B、C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )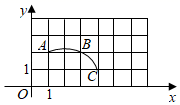 A、点(5,0) B、点(2,3) C、点(6,1) D、点(1,3)3. 如图,P为半径是3的圆O外一点,PA切圆O于A,若AP=4,则OP=( )
A、点(5,0) B、点(2,3) C、点(6,1) D、点(1,3)3. 如图,P为半径是3的圆O外一点,PA切圆O于A,若AP=4,则OP=( ) A、2 B、3 C、4 D、54. 如图,矩形ABCD中,AB=12,BC=18.将矩形沿EF折叠,使点A落在CD边中点M处,点B落在N处.连接EM,以矩形对称中心O为圆心的圆与EM相切于点P,则圆的半径为( )
A、2 B、3 C、4 D、54. 如图,矩形ABCD中,AB=12,BC=18.将矩形沿EF折叠,使点A落在CD边中点M处,点B落在N处.连接EM,以矩形对称中心O为圆心的圆与EM相切于点P,则圆的半径为( ) A、2.7 B、5.4 C、4.5 D、3.65. 如图,在 APBC中,∠C=40°,若⊙O与PA,PB相切于点A,B,则∠CAB=( )
A、2.7 B、5.4 C、4.5 D、3.65. 如图,在 APBC中,∠C=40°,若⊙O与PA,PB相切于点A,B,则∠CAB=( ) A、40° B、50° C、60° D、70°6. 如图,PA、PB分别切⊙O于点A、B,且PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长为( )
A、40° B、50° C、60° D、70°6. 如图,PA、PB分别切⊙O于点A、B,且PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长为( ) A、32 B、24 C、16 D、87. 如图,CD是Rt△ABC斜边AB上的高,AC=8,BC=6,点O是CD上的动点,以O为圆心作半径为1的圆,若该圆与△ABC重叠部分的面积为π,则OC的最小值为( )
A、32 B、24 C、16 D、87. 如图,CD是Rt△ABC斜边AB上的高,AC=8,BC=6,点O是CD上的动点,以O为圆心作半径为1的圆,若该圆与△ABC重叠部分的面积为π,则OC的最小值为( ) A、 B、 C、 D、8. 下列命题中:①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③垂直于半径的直线是圆的切线;④E,F是∠AOB的两边OA,OB上的两点,则不同的E,O,F三点确定一个圆:其中正确的有( )A、1个 B、2个 C、3个 D、0个9. 如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )
A、 B、 C、 D、8. 下列命题中:①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③垂直于半径的直线是圆的切线;④E,F是∠AOB的两边OA,OB上的两点,则不同的E,O,F三点确定一个圆:其中正确的有( )A、1个 B、2个 C、3个 D、0个9. 如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )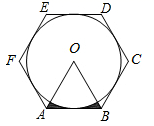 A、 B、 C、 D、10. 如图,PA,PB是⊙O的切线,A,B是切点,若 ,则 ( )
A、 B、 C、 D、10. 如图,PA,PB是⊙O的切线,A,B是切点,若 ,则 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图, 是 的切线,切点为 是 的直径, 交 于点 ,连接 ,若 ,则 的度数为 .
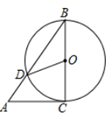 12. 如图,AB是 的直径,PA切 于点A , 线段PO交 于点C . 连接BC , 若 ,则 .
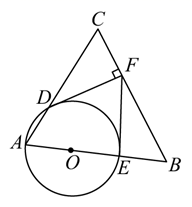
12. 如图,AB是 的直径,PA切 于点A , 线段PO交 于点C . 连接BC , 若 ,则 . 13. 如图,已知圆O为Rt△ABC的内切圆,切点分别为D、E、F,且∠C=90°,AB=13,BC=12,则圆O的半径为。
13. 如图,已知圆O为Rt△ABC的内切圆,切点分别为D、E、F,且∠C=90°,AB=13,BC=12,则圆O的半径为。 14. 如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠B+∠D=°.
14. 如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠B+∠D=°. 15. 如图,⊙O的半径为2,圆心O到直线l的距离为4,有一内角为60°的菱形,当菱形的一边在直线l上,另有两边所在的直线恰好与⊙O相切,此时菱形的边长为 .
15. 如图,⊙O的半径为2,圆心O到直线l的距离为4,有一内角为60°的菱形,当菱形的一边在直线l上,另有两边所在的直线恰好与⊙O相切,此时菱形的边长为 . 16. 如图,在矩形ABCD中,AB=8,BC=6,以顶点C为圆心,BC长为半径画圆弧BH,过AB中点P作弧BH的切线PE,E为切点,连接AE并延长交CD于点F,则tan∠DAF的数值为.
16. 如图,在矩形ABCD中,AB=8,BC=6,以顶点C为圆心,BC长为半径画圆弧BH,过AB中点P作弧BH的切线PE,E为切点,连接AE并延长交CD于点F,则tan∠DAF的数值为.
三、解答题
-
17. 如图,AB是⊙O的直径,PB是⊙O的切线,连接AP交⊙O于点C。点D在⊙O上,∠CDB=45°,求证:AB=BP。
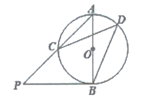 18. 如图①, 是 的弦, ,垂足为P , 交 于点E , 且 , .
18. 如图①, 是 的弦, ,垂足为P , 交 于点E , 且 , .
(Ⅰ)求 的半径;
(Ⅱ)如图②,过点E作 的切线 ,连接 并延长与该切线交于点D , 延长 交 于C , 求 的长.
19. 已知AB为 的直径,EF切 于点D , 过点B作 于点H交 于点C , 连接BD .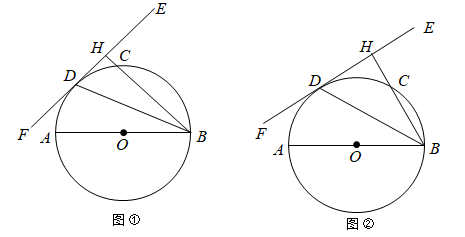 (1)、如图①,若 ,求 的大小;(2)、如图②,若C为弧BD的中点,求 的大小.
(1)、如图①,若 ,求 的大小;(2)、如图②,若C为弧BD的中点,求 的大小.四、综合题
-
20. 已知, 内接于 ,AD、BD为 的弦,且 .
 (1)、如图1,求证: ;(2)、如图2,过B作 的切线交AC的延长线于E,求证: ;(3)、如图3,在(2)的条件下,连接CD,若 , , ,求CE的长度.
(1)、如图1,求证: ;(2)、如图2,过B作 的切线交AC的延长线于E,求证: ;(3)、如图3,在(2)的条件下,连接CD,若 , , ,求CE的长度.