湘教版初中数学九年级下册2.5.1直线与圆的位置关系 同步练习

试卷更新日期：2021-12-23 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. ⊙O的半径为6cm，圆心O到直线l的距离为7cm，则直线l与⊙O的位置关系是（    ）
    A、相交 B、相切 C、相离 D、不能确定

    查看试题解析

  • 2. 已知半径为10cm的⊙O，圆心O到直线l的距离为10cm，则直线l与⊙O的位置关系是（   ）
    A、相切 B、相交 C、相离 D、相切或相交

    查看试题解析

  • 3. 在 △ABC 中， AB=AC=5 ， BC=8 ，以 A 为圆心作一个半径为3的圆，下列结论中正确的是（  ）
    A、点 B 在 ⊙A 内 B、点 C 在 ⊙A 上 C、直线 BC 与 ⊙A 相切 D、直线 BC 与 ⊙A 相离

    查看试题解析

  • 4. 如图，将直角三角板的直角顶点B放在 ⊙O 上，直角边 AB 经过圆心O，则另一直角边 BC 与 ⊙O 的位置关系为（    ）

    A、相交 B、相切 C、相离 D、无法确定

    查看试题解析

  • 5. 在平面直角坐标系中，以点 A(2 ， 1) 为圆心，1为半径的圆与 x 轴的位置关系是（    ）
    A、相离 B、相切 C、相交 D、不确定

    查看试题解析

  • 6. 已知⊙O的半径为5，直线l与⊙O相交，点O到直线l的距离为3，则⊙O上到直线l的距离为2的点共有（   ）
    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 7. 已知 ⊙O 的圆心O到直线l的距离为5， ⊙O 的半径为3，则直线l和 ⊙O 的位置关系为（   ）
    A、相离 B、相切 C、相交 D、相交或相切

    查看试题解析

  • 8. 已知同一平面内有⊙O和点A与点B ， 如果O的半径为3cm，线段OA＝5cm，线段OB＝3cm，那么直线AB与⊙O的位置关系为（　　）
    A、相离 B、相交 C、相切 D、相交或相切

    查看试题解析

  • 9. 已知⊙O的直径为4，点O到直线m的距离为2，则直线m与⊙O的位置关系是（　　）
    A、相交 B、相切 C、相离 D、无法判断

    查看试题解析

  • 10. 如图，把太阳与地平线分别抽象成圆和直线，则该图所呈现的直线与圆之间的位置关系是（　　）

    A、相切 B、相交 C、相离 D、相似

    查看试题解析

二、填空题

  • 11. 已知直线 l：y=−12x+2 ，若 ⊙P 的半径为1，圆心P在y轴上，当 ⊙P 与直线l相切时，则点P的坐标是 ．

    查看试题解析

  • 12. 如图，在 RtΔABC 中， ∠C=90° ， ∠B=30° ， AC=2 ，以C为圆心，r为半径作圆.若该圆与线段 AB 只有一个交点，则r的取值范围为.

    查看试题解析

  • 13. 圆的直径是 10cm ，如果圆心与直线的距离是 6cm ，那么该直线和圆的位置关系是.

    查看试题解析

  • 14. 如图，⊙O的半径OC=10cm ， 直线l⊥OC ， 垂足为H ， 且l交⊙O于A ， B两点，AB=16cm ， 则l沿OC所在直线向下平移cm时与⊙O相切．

    查看试题解析

  • 15. 已知⊙O的半径为8，圆心O到直线l的距离是6，则直线l与⊙O的位置关系是

    查看试题解析

  • 16. 如图，给定一个半径长为2的圆，圆心 O 到水平直线 l 的距离为 d ，即 OM=d ．我们把圆上到直线 l 的距离等于1的点的个数记为 m ．如 d=0 时， l 为经过圆心 O 的一条直线，此时圆上有四个到直线 l 的距离等于 1 的点，即 m=4 ．当 m=2 时， d 的取值范围是 ．

    查看试题解析

三、解答题

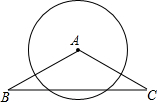
  • 17. 如图，在△ABC中，AB=AC=10，BC=16，⊙A的半径为7，判断⊙A与直线BC的位置关系，并说明理由.

    查看试题解析

  • 18. 如图，在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝4cm，以点C为圆心，以2cm长为半径作圆，试判断⊙C与AB的位置关系．

    查看试题解析

  • 19. 如图所示，Rt△ABC中，∠ACB=90°，CA=6，CB=8，以C为圆心，r为半径作⊙C，当r为多少时，⊙C与AB相切？

    查看试题解析

四、综合题

  • 20. 如图，Rt△ABC中，∠C=90°，AC=3，AB=5，若以C为圆心，r为半径作圆，那么：


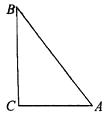    (1)、当直线AB与⊙C相切时，求r的取值范围；
    (2)、当直线AB与⊙C相离时，求r的取值范围；
    (3)、当直线AB与⊙C相交时，求r的取值范围．

    查看试题解析

  • 21. 如图，P为正比例函数y= 32 x图象上的一个动点，☉P的半径为3，设点P的坐标为(x，y).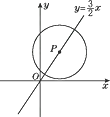

    (1)、求☉P与直线x=2相切时点P的坐标；
    (2)、请直接写出☉P与直线x=2相交、相离时，x的取值范围.

    查看试题解析

  • 22. 如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点M在AC边上，点N从点C出发沿折线CB﹣BA运动到点A停止，点P是点C关于直线MN的对称点，连接MP，NP（当点N与点C，A重合时，点P均与点C重合）．

    (1)、若CM=2，

    ①又当点N在CB上，MP∥BC时，则CN= ， MN=；

    (2)、在（1）的条件下，求点P到AB边的距离的最小值，并求出当取得这个最小值时，点P运动路线的长是多少？（参考数据：sin54°=cos36°≈ 45 ，sin36°=cos54°≈ 35 ，结果保留π）
    (3)、设MC=a（a＞2），其他条件不变，当有且只能有唯一的点P落在线段AB上时，直接写出a的取值范围 ．

    查看试题解析