湘教版初中数学九年级下册2.4过不共线三点作圆同步练习

试卷更新日期：2021-12-23 类型：同步测试

进入出卷网下载

一、单选题

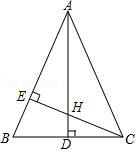
1. 如图，AB＝AD＝6，∠A＝60°，点C在∠DAB内部且∠C＝120°，则CB＋CD的最大值（）

A、4 $\sqrt{3}$ B、8 C、10 D、6 $\sqrt{3}$

查看试题解析
2. 下列命题中，正确的命题是（）

A、三角形的外心是三角形三边中垂线的交点 B、三点确定一个圆 C、平分一条弦的直径一定重直于弦 D、相等的两个圆心角所对的两条弧相等

查看试题解析
3. 如图，在 $R t Δ A B C$ 中， ∠ACB=90°， $A C = 8$ cm， $B C = 3$ cm. $D$ 是 $B C$ 边上的一个动点，连接 $A D$ ，过点 $C$ 作 $C E ⊥ A D$ 于 $E$ ，连接 $B E$ ，在点 $D$ 变化的过程中，线段 $B E$ 的最小值是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

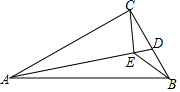查看试题解析
4. 如图，A、B、C是⊙O上的点，且∠ACB＝140°.在这个图中，画出下列度数的圆周角：40°，50°，90°，140°，仅用无刻度的直尺能画出的有（　　）

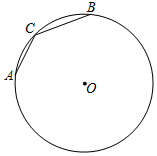A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 给出下列命题：①弦是直径；②半圆是弧；③长度相等的两段弧是等弧；④圆上两点间的线段叫弧；⑤过圆心的线段是直径；⑥直角三角形的三个顶点在同一个圆上.其中正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
6. 下列说法正确的是（）

A、垂直于弦的直线必须过圆心 B、平分弦的直径垂直于弦 C、平分弧的直径平分弧所对的弦 D、三点确定一个圆

查看试题解析
7. 在平面直角坐标系中，已知点A（0，1），B（0，﹣5），若在x轴正半轴上有一点C，使∠ACB＝30°，则点C的横坐标是（）

A、3 $\sqrt{3} +$ 4 $\sqrt{2}$ B、12 C、6+3 $\sqrt{3}$ D、6 $\sqrt{3}$

查看试题解析
8. 有一题目：“已知，点 $O$ 为 $△ A B C$ 的外心， $∠ B O C = 130 °$ ，求 $∠ A$ .”
嘉嘉的解答为：如图，画 $△ A B C$ 以及它的外接圆 $⊙ O$ ，连接 $O B$ ， $O C$ .由 $∠ B O C = 2 ∠ A = 130 °$ ，得 $∠ A = 65 °$ .

淇淇说：“嘉嘉考虑的不周全， $∠ A$ 还应有另一个不同的值.”

下列判断正确的是（）

A、淇淇说的对，且 $∠ A$ 的另一个值是115° B、淇淇说的不对， $∠ A$ 就得65° C、嘉嘉求的结果不对， $∠ A$ 应得80° D、两人都不对， $∠ A$ 应有3个不同的值

查看试题解析
9. 在锐角△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，有以下结论： $\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2 R$ （其中R为△ABC的外接圆半径）成立.在△ABC中，若∠A=75°，∠B=45°，c=4，则△ABC的外接圆面积为（）

A、 $\frac{16 π}{3}$ B、 $\frac{64 π}{3}$ C、 $16 π$ D、 $64 π$

查看试题解析
10. 如图，△ABC内接于⊙O，∠BAC＝120°，AB＝AC＝4，BD为⊙O的直径，则⊙O的半径为（）

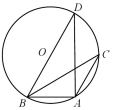A、4 B、6 C、8 D、12

查看试题解析

二、填空题

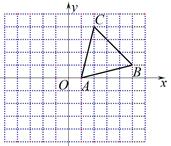
11. 如图，在平面直角坐标系中，A（0，4），B（4，4），C（6，2）．

（Ⅰ）若经过A、B、C三点的圆弧所在圆的圆心为M ，

点M的坐标为；⊙M的半径为；

（Ⅱ）若画出该圆弧所在圆，则在整个平面直角坐标系网格中该圆共经过个格点．

查看试题解析
12. 在直角坐标系中，抛物线y=ax²－4ax＋2(a>0)交y轴于点A，点B是点A关于对称轴的对称点，点C是抛物线的顶点，若△ABC的外接圆经过原点O，则a的值为.

查看试题解析
13. 已知△ABC三边长分别为5cm，12cm，13cm，则这个三角形的外接圆的半径＝.

查看试题解析
14. 如图，∠MON＝45°，一直角三角尺△ABC的两个顶点C、A分别在OM，ON上移动，若AC＝6，则点O到AC距离的最大值为.

查看试题解析
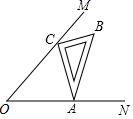15. 如图，在每个小正方形的边长为1的网格中， $△ A B C$ 的顶点A ， B在格点上，C是小正方形边的中点．

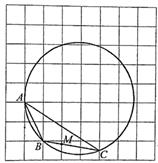(1)、 $A B$ 的长等于；

(2)、M是线段 $B C$ 与网格线的交点，P是 $△ A B C$ 外接圆上的动点，点N在线段 $P B$ 上，且满足 $P N = 2 B N$ ．当 $M N$ 取得最大值时，请在如图所示的网格中，用无刻度的直尺，画出点P ，并简要说明点P的位置是如何找到的（不要求证明）．

查看试题解析
16. $△ A B C$ 中， $A B = 9 cm$ ， $A C = 40 cm$ ， $B C = 41 cm$ ，则 $△ A B C$ 的外接圆半径长是．

查看试题解析

三、解答题

17. “不在同一直线上的三点确定一个圆”．请你判断平面直角坐标系内的三个点A(2，3)，B(－3，－7)，C(5，11)是否可以确定一个圆．

查看试题解析
18. “不在同一直线上的三点确定一个圆”．请你判断平面直角坐标系内的三个点A（2，3），B（﹣3，﹣7），C（5，11）是否可以确定一个圆．

查看试题解析
19. 已知直线l：y=x+4和点A（0，4），B（﹣4，0），设点C为直线l上一点，判断A，B，C是否在同一个圆上．

查看试题解析

四、综合题

20. 若x、x＋1、5为一个直角三角形的三条边长，回答下列问题：

(1)、求x的值；

(2)、求此三角形外接圆的半径．

查看试题解析
21. 将图中的破轮子复原，已知弧上三点A，B，C.

(1)、用尺规作出该轮的圆心O，并保留作图痕迹；

(2)、若 $△ A B C$ 是等腰三角形，设底边 $B C = 8$ ，腰 $A B = 5$ ，求圆片的半径R.

查看试题解析
22. 已知：如图， $△ A B C$ 的高 $A D$ 、 $C E$ 相交于点 $H$ ， $∠ B A C = 45 °$ .

(1)、求证： $△ A E H ≌ △ C E B$ .

(2)、若 $A H = \sqrt{2}$ ，求 $△ A B C$ 的外接圆半径.

查看试题解析
23. 如图，平面直角坐标系中，△ABC的顶点分别是A(1，0)，B(5，1)，C(2，4)

(1)、请画出△ABC绕点A逆时针旋转90°所得的△AB₁C₁ ，并写出点C₁的坐标；

(2)、在(1)的条件下，直接写出△BB₁C₁的外接圆圆心的坐标.

查看试题解析

湘教版初中数学九年级下册2.4过不共线三点作圆 同步练习

一、单选题

二、填空题

三、解答题

四、综合题

湘教版初中数学九年级下册2.4过不共线三点作圆同步练习