初中数学浙教版七年级上册期末复习专题:图形的初步知识
试卷更新日期:2021-12-23 类型:复习试卷
一、单选题
-
1. 已知点C是线段AB的中点,下列说法:①AB=2AC;②BC= AB;③AC=BC.其中正确的个数是( )A、0 B、1 C、2 D、32. 把 用度、分、秒表示,正确的是( )A、 B、 C、 D、3. 如图,将一块三角形木板截去一部分后,发现剩余木板的周长要比原三角形木板的周长大,能正确解释这一现象的数学知识是( )
 A、两直线相交只有一个交点 B、两点确定一条直线 C、经过一点有无数条直线 D、两点之间,线段最短4. 如图,从小明家A到学校B原有三条路线:路线①A﹣D﹣B;路线②A﹣E﹣B;路线③A﹣C﹣B , 后又开通了一条直道,路线④A﹣B , 这四条路线中路程最短的是( )
A、两直线相交只有一个交点 B、两点确定一条直线 C、经过一点有无数条直线 D、两点之间,线段最短4. 如图,从小明家A到学校B原有三条路线:路线①A﹣D﹣B;路线②A﹣E﹣B;路线③A﹣C﹣B , 后又开通了一条直道,路线④A﹣B , 这四条路线中路程最短的是( )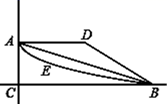 A、路线① B、路线② C、路线③ D、路线④5. 如图,下列说法错误的是( )
A、路线① B、路线② C、路线③ D、路线④5. 如图,下列说法错误的是( ) A、 是一个平角 B、 也可以表示为 C、 也可以表示为 D、 也可以表示为6. 下列几何体中,面的个数最多的是( )A、
A、 是一个平角 B、 也可以表示为 C、 也可以表示为 D、 也可以表示为6. 下列几何体中,面的个数最多的是( )A、 B、
B、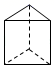 C、
C、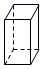 D、
D、 7. 如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能正确解释这一现象的数学知识是( )
7. 如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能正确解释这一现象的数学知识是( ) A、两点之间,直线最短 B、经过一点,有无数条直线 C、两点确定一条直线 D、两点之间,线段最短8. 如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( )
A、两点之间,直线最短 B、经过一点,有无数条直线 C、两点确定一条直线 D、两点之间,线段最短8. 如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( ) A、AB= AC B、EC=2BD C、B是AE的中点 D、DE= AB9. 已知∠AOB=30°,∠BOC=45°,则∠AOC等于( )A、15° B、75° C、15°或75° D、不能确定10. 如图,已知四条线段 , , , 中的一条与挡板另一侧的线段 在同一直线上,请借助直尺判断该线段是( )
A、AB= AC B、EC=2BD C、B是AE的中点 D、DE= AB9. 已知∠AOB=30°,∠BOC=45°,则∠AOC等于( )A、15° B、75° C、15°或75° D、不能确定10. 如图,已知四条线段 , , , 中的一条与挡板另一侧的线段 在同一直线上,请借助直尺判断该线段是( ) A、 B、 C、 D、11. 如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A、 B、 C、 D、11. 如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( ) A、1个 B、2个 C、3个 D、4个12. 已知∠A= ,∠B=30.45°,则∠A( )∠BA、 B、 C、= D、无法确定13. 如图, 与 之间的关系是( )
A、1个 B、2个 C、3个 D、4个12. 已知∠A= ,∠B=30.45°,则∠A( )∠BA、 B、 C、= D、无法确定13. 如图, 与 之间的关系是( ) A、 B、 C、 D、 与 的大小无法比较
A、 B、 C、 D、 与 的大小无法比较二、填空题
-
14. 电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,这说明(请填入符合题意答案的序号).
①点动成线;②线动成面;③面动成体.
15. 已知点C是直线AB上一点,且AC:BC=7:3,若AB=10,则AC= .16. 如图,点C,D在线段AB上,且AD=BC,则ACBD(填“>”、“<”或“=”). 17. 如图,C,D是线段AB上两点,CB=3cm,DB=5cm,D是AC的中点,则线段AB的长为cm.
17. 如图,C,D是线段AB上两点,CB=3cm,DB=5cm,D是AC的中点,则线段AB的长为cm. 18. ∠1和∠2互余,∠2和∠3互补,∠1=63°,∠3= .19. 往返于甲、乙两地的客车,中途停靠4个车站(来回票价一样),且任意两站间的票价都不同,共有种不同的票价,需准备种车票.20. 如图,直线 、 相交于点 , ,垂足为点 , ,则 .
18. ∠1和∠2互余,∠2和∠3互补,∠1=63°,∠3= .19. 往返于甲、乙两地的客车,中途停靠4个车站(来回票价一样),且任意两站间的票价都不同,共有种不同的票价,需准备种车票.20. 如图,直线 、 相交于点 , ,垂足为点 , ,则 . 21. 已知∠1与∠2互余,∠3与∠2互余,则∠1∠3.(填“>”,“=”或“<”)
21. 已知∠1与∠2互余,∠3与∠2互余,则∠1∠3.(填“>”,“=”或“<”)三、综合题
-
22. 如图,点C在线段AB上,点M、N分别是线段AC、BC的中点.
 (1)、若 ,求线段 的长度;(2)、若 ,其他条件不变,请猜想线段 的长度,并说明理由;(3)、若点C在线段AB的延长线上, , ,其它条件不变,则线段MN的长度会有变化吗?若有变化,请直接写出结果,不说明理由.23. 如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
(1)、若 ,求线段 的长度;(2)、若 ,其他条件不变,请猜想线段 的长度,并说明理由;(3)、若点C在线段AB的延长线上, , ,其它条件不变,则线段MN的长度会有变化吗?若有变化,请直接写出结果,不说明理由.23. 如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
 (1)、如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;(2)、如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.24. 如图,C为线段 上一点,点B为CD的中点,且
(1)、如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;(2)、如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.24. 如图,C为线段 上一点,点B为CD的中点,且 (1)、图中共有条线段;(2)、求 的长;(3)、若点E在直线 上,且 ,则 的长为 .25. 点 在直线 上, 为射线, .
(1)、图中共有条线段;(2)、求 的长;(3)、若点E在直线 上,且 ,则 的长为 .25. 点 在直线 上, 为射线, . (1)、如图(1),求 的度数;(2)、如图(2),点 在直线 上方, 与 互余, 平分 ,求 的度数.26. 已知点C,D是线段AB上两点,点M,N分别为AC,DB的中点.
(1)、如图(1),求 的度数;(2)、如图(2),点 在直线 上方, 与 互余, 平分 ,求 的度数.26. 已知点C,D是线段AB上两点,点M,N分别为AC,DB的中点. (1)、如图,若点C在点D的左侧,AB=12,CD=5,求MN的长.(2)、若AB=a,CD=b,请直接用含a,b的式子表示MN的长.27. 如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.
(1)、如图,若点C在点D的左侧,AB=12,CD=5,求MN的长.(2)、若AB=a,CD=b,请直接用含a,b的式子表示MN的长.27. 如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒. (1)、当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间有何数量关系 ;(2)、若射线OC的位值保持不变,且∠COE=140°
(1)、当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间有何数量关系 ;(2)、若射线OC的位值保持不变,且∠COE=140°①在旋转的过程中,是否存在某个时刻,使得射线OA,OC,OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请直接写出所有满足题意t的取值 ,若不存在,请说明理由;
②在旋转的过程中,当边AB与射线OE相交时,如图3,请直接写出∠AOC﹣∠BOE的值 .
28.(1)、(问题)如图①,点C是线段AB上一点,点D,E分别是线段AC,BC的中点,若线段AB=26cm,则线段DE的长为 cm. (2)、(拓展)在(问题)中,若把条件“如图①,点C是线段AB上一点”改为“点C是直线 AB上一点”,其余条件不变,则(问题)中DE的长是否会发生变化?请画出示意图并求解.(3)、(应用)如图②,∠AOB=α,点C在∠AOB内部,射线OM,ON分别平分∠AOC,∠BOC,则∠MON的大小为(用含字母α的式子表示).
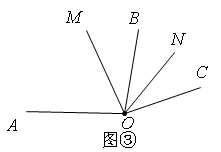
(2)、(拓展)在(问题)中,若把条件“如图①,点C是线段AB上一点”改为“点C是直线 AB上一点”,其余条件不变,则(问题)中DE的长是否会发生变化?请画出示意图并求解.(3)、(应用)如图②,∠AOB=α,点C在∠AOB内部,射线OM,ON分别平分∠AOC,∠BOC,则∠MON的大小为(用含字母α的式子表示).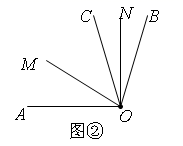 (4)、如图③,在(3)中,若点C在∠AOB外部,且射线OC与射线OB在OA所在直线的同侧,其他条件不变,则(1)中的结论是否成立,若成立,请写出求解过程;若不成立,请说明理由.
(4)、如图③,在(3)中,若点C在∠AOB外部,且射线OC与射线OB在OA所在直线的同侧,其他条件不变,则(1)中的结论是否成立,若成立,请写出求解过程;若不成立,请说明理由.