浙教版初数九上期末冲刺必刷提分题（精选押题）

试卷更新日期：2021-12-23 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，在△ABC中，以B为圆心，BC为半径作弧，分别交AC，AB于点D，E，连接DE，若ED＝DC，AD＝3，AE＝2，则△AED与四边形BCDE的面积之比是（）

A、9：14 B、2：5 C、6：7 D、3：7

查看试题解析
2. 如图，△ABC中，∠ABC＝90°，AB＝2，AC＝4，点O为BC的中点，以O为圆心，OB长为半径作半圆，交AC于点D，则图中阴影部分的面积是（）

A、 $\frac{5}{4} \sqrt{3} - \frac{π}{2}$ B、 $5 \sqrt{3} - \frac{3}{2} π$ C、 $2 \sqrt{3} - \frac{π}{2}$ D、 $\frac{2}{3} \sqrt{3} π$

查看试题解析
3. 如图，在5×3的网格图中，每个小正方形的边长均为1，设经过图中格点A，C，B三点的圆弧与BD交于E，则图中阴影部分的面积为（）（结果保留π）

A、 $\frac{5}{4}$ π- $\frac{5}{8}$ B、 $\frac{5}{3}$ C、 $\frac{13}{16}$ π- $\frac{13}{8}$ D、 $\frac{5}{3}$ π

查看试题解析
4. 如图，函数 $y = - x^{2} + 12$ 的图象与x轴交于A，B两点，点C是以 $M (0 ， 2)$ 为圆心，2为半径的圆上的动点，P是 $A C$ 的中点，连结 $O P$ ，则线段 $O P$ 的最小值是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $\sqrt{7}$

查看试题解析
5. 如图，BC为⊙O的直径，AB交⊙O于E点，AC交⊙O于D点，AD＝CD，∠A＝70°，则∠BOE的度数是（）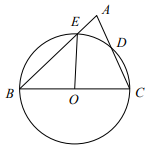

A、140° B、100° C、90° D、80°

查看试题解析
6. 如图，在Rt△ABC中，∠ABC=90°，AB=BC，点P在△ABC内一点，连接PA，PB，PC，若∠BAP=∠CBP，且AP = 6，则PC的最小值是（）

A、 $2 \sqrt{2}$ B、 $3$ C、 $3 \sqrt{5} - 3$ D、 $3 \sqrt{2}$

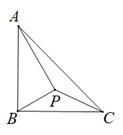查看试题解析
7. 如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上(不与点A，点C重合)，BD与OA交于点E，设∠AED=α，∠AOD=β，则（）

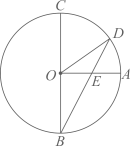A、3α+β=180° B、2α+β=180° C、3α-β=90° D、2α-β=90°

查看试题解析
8. 如图，在平面直角坐标系 $x O y$ 中，函数 $y = a x^{2} + b x + c$ 的图像与对称轴直线 $x = m$ 交于点A，与 $x ， y$ 轴交于 $B ， C ， D$ 三点，下列命题正确的是（）
① $a b c > 0$ ；②若 $O D = O C$ ，则 $a c + b + 1 = 0$ ；③对于任意 $x_{0} (x_{0} \neq m)$ ，始终有 $a x_{0}^{2} + b x_{0} > a m^{2} + b m$ ；④若B的坐标为 $(- m ， 0)$ ，则C的坐标为 $(3 m ， 0)$ ．

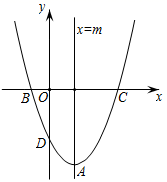A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
9. 已知点(x₀ ， y₀)是二次函数y＝ax²＋bx＋c(a≠0)的图象上一个定点，而(m ， n)是二次函数图象上动点，若对任意的实数m ，都有a(y₀－n)≤0，则以x₀为根的关于t的方程是（）

A、at－2b＝0 B、at＋2b＝0 C、2at－b＝0 D、2at＋b＝0

查看试题解析
10. 如图所示，二次函数 $y = a x^{2} + b x + c$ 的图象与x轴负半轴相交与A、B两点， $Q (n ， \frac{1}{2})$ 是二次函数 $y = a x^{2} + b x + c$ 图象上的一点，且 $A Q ⊥ B Q$ ，则 $a$ 的值为（）

A、 B、 C、 $- \frac{1}{3}$ D、 $- \frac{1}{2}$

查看试题解析
11. 已知二次函数y=ax²+bx+c（a≠0）的图象如图，有下列5个结论：①4a+2b+c＞0；②abc＜0；③b＜a﹣c；④3b＞2c；⑤a+b＜m（am+b），（m≠1的实数）；其中正确结论的个数为（）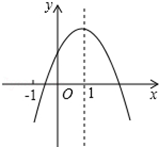

A、2个 B、3个 C、4个 D、5个

查看试题解析
12. 如图，已知抛物线y＝x²+bx+c与直线y＝x交于（1，1）和（3，3）两点，现有以下结论：①b²﹣4c＞0；②3b+c+6＝0；③当x²+bx+c＞ $\frac{2}{x}$ 时，x＞2；④当1＜x＜3时，x²+（b﹣1）x+c＜0，其中正确的序号是（）

A、①②④ B、②③④ C、②④ D、③④

查看试题解析
13. 如图，已知A(0，2)，B(1，0)，C(2，1)，若抛物线y=x²+bx+1与△ABC的边一定有公共点，则b的取值范围是（）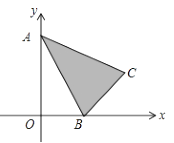

A、b≤0 B、b≤-2 C、b $\geq$ 0 D、b $\geq$ -2

查看试题解析
14. 二次函数y=ax²+bx+c（a≠0）的部分图象如图所示，图象过点（-1，0），对称轴为直线X=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（-3，y₁）、点B（ $- \frac{1}{2}$ ，y₂）、点C（ $\frac{7}{2}$ ，y₃）在该函数图象上，则y₁＜y₃＜y₂；（5）若方程a（x+1）（x-5）=-3的两根为x₁和x₂ ，且x₁＜x₂ ，则x₁＜-1＜5＜x₂ ．其中正确的结论有（）个．

A、2个 B、3个 C、4个 D、5个

查看试题解析
15. 如图， $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $\cos B = \frac{1}{4}$ ，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，使 $∠ A D E = ∠ B$ ，连结CE，则 $\frac{C E}{A D}$ 的值为（）

A、 $\frac{3}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{15}}{2}$ D、2

查看试题解析
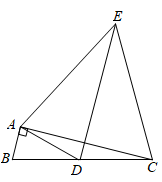16. 如图，在等边三角形ABC的AC，BC边上分别任取一点P，Q，且AP=CQ，AQ、BP相交于点O。下列四个结论：①若PC=2AP，则BO=6OP；②若BC=8，BP=7，则PC=5；③AP²=OP·AQ；④若AB=3，则OC的最小值为 $\sqrt{3}$ ，其中正确的是（）

A、①②④ B、①③④ C、②③④ D、①②③

查看试题解析
17. 如图，AD∥BC，∠D=90°，AD=2，BC=5，DC=11，若在边DC上有点P，使△PAD与△PBC相似，则这样的点P有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
18. 如图，正方形ABCD的边长AB=8，E为平面内一动点，且AE=4，F为CD上一点，CF=2，连接EF，ED，则2EF+ED的最小值为（）

A、12 $\sqrt{3}$ B、12 $\sqrt{2}$ C、12 D、10

查看试题解析
19. 如图，AB是半圆的直径，点C是弧AB的中点，点E是弧AC的中点，连结EB，CA交于点F，则的值为（）

A、 $\frac{1}{4}$ B、 $\frac{2 - \sqrt{2}}{4}$ C、 $1 - \frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{2} - 1}{2}$

查看试题解析
20. 如图，△ABC内接于⊙O，BC=6，AC=2，∠A-∠B=90°，则⊙O的面积为（）

A、9.6π B、10π C、10.8π D、12π

查看试题解析
21. 如图，⊙O上有一个动点A和一个定点B，令线段AB的中点是点P，过点B作⊙O的切线BQ，且BQ=3，现测得 $\overset{⌢}{A B}$ 的长度是 $\frac{4 π}{3}$ ， $\overset{⌢}{A B}$ 的度数是120°，若线段PQ的最大值是m，最小值是n，则mn的值是（　　）

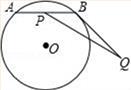A、3 $\sqrt{10}$ B、2 $\sqrt{13}$ C、9 D、10

查看试题解析
22. 如图，在等腰Rt△ABC中，∠BAC＝90°，BC＝2，点P是△ABC内部的一个动点，且满足∠PBC＝∠PCA，则线段AP长的最小值为（　　）

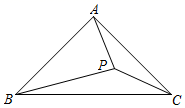A、0.5 B、 $\sqrt{2}$ ﹣1 C、2﹣ $\sqrt{2}$ D、 $\frac{1}{3}$

查看试题解析
23. 如图，在△ABC中，AC=BC=2，D是BC的中点，过A，C，D三点的⊙O与AB边相切于点A，则⊙O的半径为（）

A、 $\frac{\sqrt{7}}{3}$ B、 $\frac{2 \sqrt{5}}{5}$ C、1 D、 $\frac{2 \sqrt{14}}{7}$

查看试题解析
24. 如图，在矩形ABCD中，AB=6，AD=8，以BC为斜边在矩形所在平面作直角三角形BEC，F为CD的中点，则EF的最小值为（）

A、 $\frac{1}{2}$ B、 $1$ C、 $2$ D、 $3$

查看试题解析
25. 如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=4 $\sqrt{2}$ ，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，则线段EF长度的最小值为（）

A、 $\sqrt{6}$ B、 $2 \sqrt{6}$ C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
26. 如图，半径为4的⊙O中，CD为直径，弦AB⊥CD且过半径OD的中点，点E为⊙O上一动点，CF⊥AE于点F。当点E从点B出发顺时针运动到点D时，点F所经过的路径长为（）

A、 $\sqrt{3} π$ B、 $\frac{\sqrt{3}}{2} π$ C、 $\frac{2 \sqrt{3}}{3} π$ D、 $\frac{\sqrt{3}}{3} π$

查看试题解析
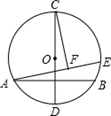27. 如图，已知正方形ABCD的边长是4，点E是AB边上一动点，连接CE，过点B作BG⊥CE于点G，点P是AB边上另一动点，则PD+PG的最小值是（）

A、 $2 \sqrt{10} - 2$ B、 $4 \sqrt{3} - 2$ C、 $2 \sqrt{13} - 2$ D、 $2 \sqrt{14} - 2$

查看试题解析

二、填空题

28. 如图是一张矩形纸片，E是AB的中点，把△BCE沿直线CE对折，使点B落在对角线BD上的点F处，AB＝2，则CB＝．

查看试题解析
29. 如图，△A′B′C是由△ABC旋转而成，连接AA′、BB′交点为F，若∠ABC = 90°，∠BFA=25°，则∠BAC = ．

查看试题解析
30. 如图，⊙O的半径为2，△ABC内接于⊙O，若∠A＝60°，∠C＝45°，则AC＝．

查看试题解析
31. 如图，已知：PA＝2，PB＝4，以AB为边作正方形ABCD，使P、D两点落在直线AB的两侧．当∠APB＝45°时，则PD的长为．

查看试题解析
32. 如图，四边形ABCD内接于⊙O，F是 $\overset{⌢}{C D}$ 上一点，且 $\overset{⌢}{D F} = \overset{⌢}{B C}$ ，连接CF并延长交AD的延长线于点E，连接AC.若∠ABC＝105°，∠BAC＝30°，则∠E的度数为度.

查看试题解析
33. 如图， $A B$ 为 $⊙ O$ 的直径，点 $D$ 是弧 $A C$ 的中点，过点 $D$ 作 $D E ⊥ A B$ 于点 $E$ ，延长 $D E$ 交 $⊙ O$ 于点 $F$ ，若 $A C = 12 ， A E = 3$ ，则 $⊙ O$ 的半径长为

查看试题解析
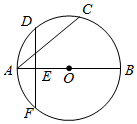34. 如图，在长方形ABCD中，点E是BC上一点，连结AE，以AE为对称轴作△ABE的轴对称图形△AB′E，延长EB′恰好经过点D，过点E作EF⊥BC，垂足为E，交AB′于点F，已知AB=9，AD=15，则EF= ．

查看试题解析
35. 如图，二次函数y=x²－2x+c的图象与x轴交于点A(3，0)，点D是y轴负半轴上一点，以OA，OD为邻边作矩形ABDO，直线BD交二次函数的图象于点C，E（点C在点D的左侧），若CD=BE，则OD的长为．

查看试题解析

三、综合题

36. 如图，在△ABC中，AB＝AC，以AC为直径的⊙O交AB于点D，交BC于点E．

(1)、求证：BE＝CE；

(2)、若BD＝3，CE＝4，求AC的长．

查看试题解析
37. 如图，AB是圆O的直径，弦CD⊥AB于点E，G是 $\overset{⌢}{A C}$ 上任意一点，连接AD，AG，GD.

(1)、求证：∠ADC＝∠AGD；

(2)、若BE＝2，CD＝8，求圆O的半径.

查看试题解析
38. 如图，⊙O是四边形ABCD的外接圆，直径BD与弦AC交于点E．若∠BAC＝2∠ABE．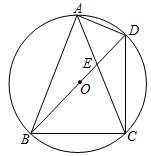

(1)、求证：AB＝AC；

(2)、当△BCE是等腰三角形时，求∠BCE的大小；

(3)、当AE＝4，CE＝6时，求边BC的长．

查看试题解析
39. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} - 6 a x + 4$ 与x轴的一个交点为 $A (- 2 ， 0)$ ，与y轴的交点为C，点B为抛物线对称轴上一动点．

(1)、抛物线的函数表达式为，抛物线的对称轴为．

(2)、线段 $B C$ 绕点B顺时针旋转 $90 °$ 得到 $B P$ ，当点P落在抛物线上时，求出点B坐标．

(3)、当点B在x轴上时，M，N是抛物线上的两个动点，M在N的右侧，若以B，C，M，N四点为顶点的四边形是平行四边形，求出此时点M的横坐标．

查看试题解析
40. 如图，在平面直角坐标系中，直线 $A B ： y = k x + 3$ 与坐标轴交于A，B两点，经过点B的抛物线 $y = a x^{2} + b x$ 交直线 $A B$ 于点 $C (2 ， 2)$ ．

(1)、求该抛物线的解析式．

(2)、在直线 $A B$ 上方的抛物线上是否存在点P，使得 $S_{△ P A O} = S_{△ P B O}$ ，若存在请求出点P的坐标，若不存在请说明理由．

查看试题解析