初中数学浙教版九年级上册期末复习专题:相似三角形
试卷更新日期:2021-12-23 类型:复习试卷
一、单选题
-
1. 如图,小明在A时测得某树的影长为4米,B时又测得该树的影长为1米,若两次日照的光线互相垂直,则树的高度为( )米.
 A、2 B、4 C、6 D、82. 如图,D、E分别是AB、AC的中点,则S△ADE:S△ABC=( )
A、2 B、4 C、6 D、82. 如图,D、E分别是AB、AC的中点,则S△ADE:S△ABC=( ) A、1:2 B、1:3 C、1:4 D、2:33. 如图,在正方形ABCD中,E为AD上的点,连接CE.①以点E为圆心,以任意长为半径作弧分别交EC,ED于点N,M;②分别以M,N为圆心,以大于 长为半径作弧,两弧在 内交于点P;③连接EP并延长交DC于点H,交BC的延长线于点G.若 , ,则EH的长为( )
A、1:2 B、1:3 C、1:4 D、2:33. 如图,在正方形ABCD中,E为AD上的点,连接CE.①以点E为圆心,以任意长为半径作弧分别交EC,ED于点N,M;②分别以M,N为圆心,以大于 长为半径作弧,两弧在 内交于点P;③连接EP并延长交DC于点H,交BC的延长线于点G.若 , ,则EH的长为( ) A、14 B、 C、16 D、4. 如图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面直径AB的长度是( )
A、14 B、 C、16 D、4. 如图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面直径AB的长度是( ) A、2cm B、2.5cm C、3cm D、4cm5. 如图,已知在△ABC纸板中,AC=4,BC=8,AB=11,P是BC上一点,沿过点P的直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是( )
A、2cm B、2.5cm C、3cm D、4cm5. 如图,已知在△ABC纸板中,AC=4,BC=8,AB=11,P是BC上一点,沿过点P的直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么CP长的取值范围是( )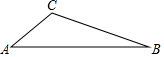 A、0<CP≤1 B、0<CP≤2 C、1≤CP<8 D、2≤CP<86. 如图,有一块锐角三角形材料,边 ,高 ,要把它加工成矩形零件,使其边在BC上,其余两个顶点分别在AB,AC上,且 ,则这个矩形零件的长为( )
A、0<CP≤1 B、0<CP≤2 C、1≤CP<8 D、2≤CP<86. 如图,有一块锐角三角形材料,边 ,高 ,要把它加工成矩形零件,使其边在BC上,其余两个顶点分别在AB,AC上,且 ,则这个矩形零件的长为( ) A、32mm B、36mm C、40mm D、44mm7. 如图,直线l1、l2、…l6是一组等距离的平行线,过直线l1上的点A作两条射线,分别与直线l3 , l6相交于点B、E、C、F.若BC=2,则EF的长是( )
A、32mm B、36mm C、40mm D、44mm7. 如图,直线l1、l2、…l6是一组等距离的平行线,过直线l1上的点A作两条射线,分别与直线l3 , l6相交于点B、E、C、F.若BC=2,则EF的长是( ) A、4 B、5 C、6 D、78. 如图,有一块形状为Rt△ABC的斜板余料,∠A=90°,AB=6cm,AC=8cm,要把它加工成一个形状为▱DEFG的工件,使GF在边BC上,D、E两点分别在边AB、AC上,若点D是边AB的中点,则S▱DEFG的面积为( )cm2 .
A、4 B、5 C、6 D、78. 如图,有一块形状为Rt△ABC的斜板余料,∠A=90°,AB=6cm,AC=8cm,要把它加工成一个形状为▱DEFG的工件,使GF在边BC上,D、E两点分别在边AB、AC上,若点D是边AB的中点,则S▱DEFG的面积为( )cm2 . A、10 B、12 C、14 D、169. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=5:2,连接AE交DB于点F , 则△DEF的面积与△BAF的面积之比为( )
A、10 B、12 C、14 D、169. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=5:2,连接AE交DB于点F , 则△DEF的面积与△BAF的面积之比为( ) A、2:5 B、25:35 C、4:25 D、25:4910. 如图,等边 中, 为 边中点, 于 , 交 于 点,则 与 的面积之比为( )
A、2:5 B、25:35 C、4:25 D、25:4910. 如图,等边 中, 为 边中点, 于 , 交 于 点,则 与 的面积之比为( ) A、 B、 C、 D、11. 如图,在 中,D、E分别是边 、 上的点, 与 相交于点F , 若E为 的中点, ,则 的值是( )
A、 B、 C、 D、11. 如图,在 中,D、E分别是边 、 上的点, 与 相交于点F , 若E为 的中点, ,则 的值是( ) A、2.5 B、3 C、4 D、212. 如图,在△ABC中,以B为圆心,BC为半径作弧,分别交AC,AB于点D,E,连接DE,若ED=DC,AD=3,AE=2,则△AED与四边形BCDE的面积之比是( )
A、2.5 B、3 C、4 D、212. 如图,在△ABC中,以B为圆心,BC为半径作弧,分别交AC,AB于点D,E,连接DE,若ED=DC,AD=3,AE=2,则△AED与四边形BCDE的面积之比是( ) A、9:14 B、2:5 C、6:7 D、3:713. 如图,在 中, , ,以点 为圆心,以 的长为半径作弧交 于点 ,连接 ,再分别以点 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,连接 ,则下列结论中错误的是 ( )
A、9:14 B、2:5 C、6:7 D、3:713. 如图,在 中, , ,以点 为圆心,以 的长为半径作弧交 于点 ,连接 ,再分别以点 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,连接 ,则下列结论中错误的是 ( )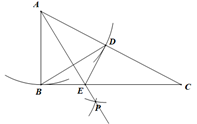 A、 B、 垂直平分线段 C、 D、14. 如图,在正方形ABCD中,点E是边BC的中点,连接AE、DE,分别交BD、AC于点P、Q,过点P作PF⊥AE交CB的延长线于F,下列结论:
A、 B、 垂直平分线段 C、 D、14. 如图,在正方形ABCD中,点E是边BC的中点,连接AE、DE,分别交BD、AC于点P、Q,过点P作PF⊥AE交CB的延长线于F,下列结论:①∠AED+∠EAC+∠EDB=90°,②AP=FP,③AE= AO,④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36,⑤CE•EF=EQ•DE.其中正确的结论有( )
 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
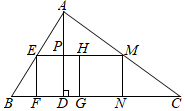
15. 如图,在 中, ,垂足为 , , ,四边形 和四边形 均为正方形,且点 、 、 、 、 、 都在 的边上,那么 与四边形 的面积比为 .
 16. 某一时刻,身高1.6m的小明在阳光下的影长是0.6m,同一时刻同一地点测得旗杆的影长是3m,则该旗杆的高度是 m.17. 在矩形ABCD中, , .点P在矩形ABCD的对角线BD上,点E在边BC上,满足 ,若 是等腰三角形,则PE的长为 .18. 如图,△ABC绕点B顺时针旋转得到△DBE,点A与点D对应,点C与点E对应,DB,DE分别与AC边交于G,F两点,连接BF,若DE垂直平分BC,下列结论:①∠E=30°;②BF⊥BE;③△ABG∽△DBF;④GF•BD=DG•BF.其中结论正确的是 . (填序号即可)
16. 某一时刻,身高1.6m的小明在阳光下的影长是0.6m,同一时刻同一地点测得旗杆的影长是3m,则该旗杆的高度是 m.17. 在矩形ABCD中, , .点P在矩形ABCD的对角线BD上,点E在边BC上,满足 ,若 是等腰三角形,则PE的长为 .18. 如图,△ABC绕点B顺时针旋转得到△DBE,点A与点D对应,点C与点E对应,DB,DE分别与AC边交于G,F两点,连接BF,若DE垂直平分BC,下列结论:①∠E=30°;②BF⊥BE;③△ABG∽△DBF;④GF•BD=DG•BF.其中结论正确的是 . (填序号即可)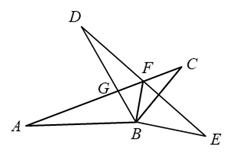 19. 如图,在平行四边形ABCD中,AC,BD相交于点O,E是OA的中点,连接BE并延长交AD于点F.
19. 如图,在平行四边形ABCD中,AC,BD相交于点O,E是OA的中点,连接BE并延长交AD于点F. (1)、 = .(2)、若△AEF的面积为4,则平行四边形ABCD的面积为 .20. 如图是小孔成像原理的示意图,点 与物体 的距离为 ,与像 的距离是 , . 若物体 的高度为 ,则像 的高度是 .
(1)、 = .(2)、若△AEF的面积为4,则平行四边形ABCD的面积为 .20. 如图是小孔成像原理的示意图,点 与物体 的距离为 ,与像 的距离是 , . 若物体 的高度为 ,则像 的高度是 . 21. 如图,在正方形 中,以 为腰向正方形内部作等腰 ( ),点 在 上,且 .连接 并延长,与 交于点 ,与 延长线交于点 .连接 交 于点 ,连接 .若 , ,则 .
21. 如图,在正方形 中,以 为腰向正方形内部作等腰 ( ),点 在 上,且 .连接 并延长,与 交于点 ,与 延长线交于点 .连接 交 于点 ,连接 .若 , ,则 . 22. 如图,矩形ABCD中,AD=2,AB=4,AC为对角线,E、F分别为边AB、CD上的动点,且EF⊥AC于点M,连接AF、CE,求AF+CE的最小值是 .
22. 如图,矩形ABCD中,AD=2,AB=4,AC为对角线,E、F分别为边AB、CD上的动点,且EF⊥AC于点M,连接AF、CE,求AF+CE的最小值是 .
三、综合题
-
23. 如图
 (1)、(基础巩固)
(1)、(基础巩固)
如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD•AB.(2)、(尝试应用)
如图2,在▱ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.24. 如图,正方形ABCD中,M为BC上点,F是AM的中点,过点F作 ,交AD的延长线于点E,交DC于点N. (1)、求证: ;(2)、若 , ,求DE的长.25. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示.
(1)、求证: ;(2)、若 , ,求DE的长.25. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示.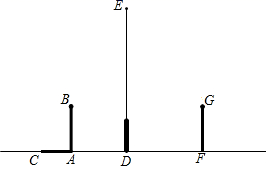 (1)、请你通过画图确定灯泡所在的位置.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.26. 如图,在Rt△ACB中,∠ACB=90°,点D为AB边上一点,且BC=CD,过D作DE⊥AB交AC于E.
(1)、请你通过画图确定灯泡所在的位置.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.26. 如图,在Rt△ACB中,∠ACB=90°,点D为AB边上一点,且BC=CD,过D作DE⊥AB交AC于E.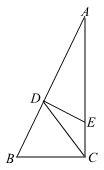 (1)、求证:△CDE∽△CAD;(2)、若BC=2,CE=1,求AD的长.27.(1)、解方程(2)、如图所示, 中, 求证:
(1)、求证:△CDE∽△CAD;(2)、若BC=2,CE=1,求AD的长.27.(1)、解方程(2)、如图所示, 中, 求证: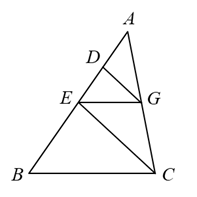 28. 已知:如图,在菱形 中,点 , 分别在边 , 上, , 的延长线交 的延长线于点 , 的延长线交 的延长线于点 .
28. 已知:如图,在菱形 中,点 , 分别在边 , 上, , 的延长线交 的延长线于点 , 的延长线交 的延长线于点 . (1)、求证: ;(2)、如果 ,求证: .
(1)、求证: ;(2)、如果 ,求证: .


