初中数学浙教版九年级上册期末复习专题:比例
试卷更新日期:2021-12-23 类型:复习试卷
一、单选题
-
1. 如图,若AB∥CD∥EF,则下列结论中,与 相等的是( )
 A、 B、 C、 D、2. 如图,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,BE与CD相交于F,则下列结论一定正确的是( ).
A、 B、 C、 D、2. 如图,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,BE与CD相交于F,则下列结论一定正确的是( ).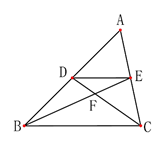 A、 B、 C、 D、3. 如图,在 中,点 , , 分别在 , , 边上, , ,则下列式子一定正确的是( )
A、 B、 C、 D、3. 如图,在 中,点 , , 分别在 , , 边上, , ,则下列式子一定正确的是( ) A、 B、 C、 D、4. 如图, 与 相交于点 ,点 在线段 上,且 .若 , , ,则 的值为( )
A、 B、 C、 D、4. 如图, 与 相交于点 ,点 在线段 上,且 .若 , , ,则 的值为( ) A、 B、 C、 D、5. 中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF,观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A、 B、 C、 D、5. 中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF,观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( ) A、 B、 C、 D、6. 若 ,则 的值是( )A、1 B、 C、3 D、无法确定7. 已知线段AB的长度为2,点C是线段AB的黄金分割点,则AC的长度为( )A、 B、 C、 或 D、 或8. 若 ,则 =( )A、12 B、 C、 D、9. 已知线段a , b , c , 其中c是a和b的比例中项,a=4,b=16,则c等于( )A、±8 B、±10 C、8 D、1010. 如图,点 是线段 的黄金分割点( ),下列结论错误的是( )
A、 B、 C、 D、6. 若 ,则 的值是( )A、1 B、 C、3 D、无法确定7. 已知线段AB的长度为2,点C是线段AB的黄金分割点,则AC的长度为( )A、 B、 C、 或 D、 或8. 若 ,则 =( )A、12 B、 C、 D、9. 已知线段a , b , c , 其中c是a和b的比例中项,a=4,b=16,则c等于( )A、±8 B、±10 C、8 D、1010. 如图,点 是线段 的黄金分割点( ),下列结论错误的是( )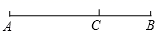 A、 B、 C、 D、11. 如果 ,则下列结论错误的是( )A、 B、 C、 D、
A、 B、 C、 D、11. 如果 ,则下列结论错误的是( )A、 B、 C、 D、二、填空题
-
12. 已知 .若 .则 的值为 .13. 某品牌汽车为了打造更加精美的外观,特将汽车倒车镜设计为整个车身黄金分割点的位置(如图),若车头与倒车镜的水平距离为1.58m,则该车车身总长约为m.(结果精确到0.01m)
 14. 如图,C、D是线段AB的两个黄金分割点,则 的值为 .
14. 如图,C、D是线段AB的两个黄金分割点,则 的值为 . 15. 如图AB∥CD∥EF,若 , ,则 .
15. 如图AB∥CD∥EF,若 , ,则 . 16. 如图,在△ABC中,点D是AB边上的一点,且AD=3BD,连接C并取CD的中点E,连接BE,若∠ACD=∠BED=45°,且CD=6 ,则AB的长为 .
16. 如图,在△ABC中,点D是AB边上的一点,且AD=3BD,连接C并取CD的中点E,连接BE,若∠ACD=∠BED=45°,且CD=6 ,则AB的长为 . 17. 如图,△ABC是等腰三角形,AB=AC=8,BC=3,点D在AB边上,点E在CB的延长线上,已知AD=3,BE=2,连接ED并延长交AC于点F , 则线段AF的长为 .
17. 如图,△ABC是等腰三角形,AB=AC=8,BC=3,点D在AB边上,点E在CB的延长线上,已知AD=3,BE=2,连接ED并延长交AC于点F , 则线段AF的长为 . 18. 如图,AB∥CD∥EF , 点C , D分别在BE , AF上,如果BC=4,CE=6,AF=8,那么DF的长 .
18. 如图,AB∥CD∥EF , 点C , D分别在BE , AF上,如果BC=4,CE=6,AF=8,那么DF的长 . 19. 如图,直线 ,它们依次交直线m、n于点A、C、E和B、D、F,已知 , , ,那么 等于 .
19. 如图,直线 ,它们依次交直线m、n于点A、C、E和B、D、F,已知 , , ,那么 等于 .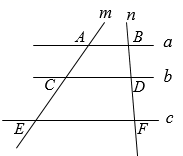 20. 如图所示,已知AB∥EF∥CD , AC , BD相交于点E , AB=3cm , CD=6cm , 则EF= .
20. 如图所示,已知AB∥EF∥CD , AC , BD相交于点E , AB=3cm , CD=6cm , 则EF= .
三、综合题
-
21. 阅读下列材料,完成任务
小明同学酷爱数学,勤于探索研究,他画了一个三角形ABC,并画出其中一个外角 的角平分线,与BC的延长线交于点N,小明通过测量发现,该图形中的线段有特殊的关系: ,他想证明自己的发现.下面是部分证明过程:
证明:过点C作 交AB于点D,则 (第一步),
∴ , (第二步)
…

请回答下面问题:
(1)、小明部分证明过程中,第一步的依据是;(2)、请完成证明的剩余部分;(3)、若 , , ,请求出CN的长.22. 如图,已知直线l1、l2、l3分别截直线l4于点A、B、C , 截直线l5于点D、E、F , 且 (1)、如果AB=3,BC=6,DE=4,求EF的长;(2)、如果DE:EF=2:3,AC=25,求AB的长.23. △ABC中,点D是BC边上的一点,点F在AD上,连接BF并延长交AC于点E;
(1)、如果AB=3,BC=6,DE=4,求EF的长;(2)、如果DE:EF=2:3,AC=25,求AB的长.23. △ABC中,点D是BC边上的一点,点F在AD上,连接BF并延长交AC于点E; (1)、如图1,若D为BC的中点, ,求证:AF=FD;(2)、尺规作图:在图2中,请利用圆规和无刻度的直尺在AC上找一点E,使得 ;(3)、若F为AD的中点,设 ,请求出m、n之间的等量关系.24. 如图1,点C在线段 上,图中共有3条线段 、 、和 ,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段 的“二倍点”.
(1)、如图1,若D为BC的中点, ,求证:AF=FD;(2)、尺规作图:在图2中,请利用圆规和无刻度的直尺在AC上找一点E,使得 ;(3)、若F为AD的中点,设 ,请求出m、n之间的等量关系.24. 如图1,点C在线段 上,图中共有3条线段 、 、和 ,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段 的“二倍点”.如图2,一次函数 与x轴交于点A,与y轴交于点B,与反比例函数 的图象位于第一象限的部分相交于点C.

 (1)、求点A的坐标;(2)、若点B是线段 的“二倍点”,则 .(直接写出结果)25. 在平面直角坐标系 中,直线 : 经过一个定点 ,直线 与反比例函数 图象相交于点 .(1)、直线 : 可以看成是直线 沿 轴向(填“左”或“右”)平移1个单位得到的,请直接写出定点 的坐标;(2)、求 的值;(3)、直线 与 轴、 轴分别交于点 , .若 ,求 的值.26.
(1)、求点A的坐标;(2)、若点B是线段 的“二倍点”,则 .(直接写出结果)25. 在平面直角坐标系 中,直线 : 经过一个定点 ,直线 与反比例函数 图象相交于点 .(1)、直线 : 可以看成是直线 沿 轴向(填“左”或“右”)平移1个单位得到的,请直接写出定点 的坐标;(2)、求 的值;(3)、直线 与 轴、 轴分别交于点 , .若 ,求 的值.26. (1)、如图①,在▱ABCD中,点E为CD的中点,连接BE并延长交AD的延长线于点F.求证:点E是BF的中点,点D是AF的中点;(2)、如图②,在四边形ABCD中,AD//BC,∠BAD=90°,AB=4,AD=3,点E是CD的中点,BE⊥CD,BE、AD的延长线相交于点F,则AF= .(3)、如图③,在△ABC中,点D是AC的中点,点E是AB上一点, ,BD,CE相交于点F,则 = .27. 如图,抛物线y= +bx+c与y轴交于点A(0,2),对称轴为直线x=2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6.
(1)、如图①,在▱ABCD中,点E为CD的中点,连接BE并延长交AD的延长线于点F.求证:点E是BF的中点,点D是AF的中点;(2)、如图②,在四边形ABCD中,AD//BC,∠BAD=90°,AB=4,AD=3,点E是CD的中点,BE⊥CD,BE、AD的延长线相交于点F,则AF= .(3)、如图③,在△ABC中,点D是AC的中点,点E是AB上一点, ,BD,CE相交于点F,则 = .27. 如图,抛物线y= +bx+c与y轴交于点A(0,2),对称轴为直线x=2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6. (1)、求此抛物线的解析式;(2)、点P在x轴上,直线BP将△ABC面积分成2:3两部分,求出P点坐标.28. 在 ABC中,∠ABC=90°, ,M是BC上一点,连接AM.
(1)、求此抛物线的解析式;(2)、点P在x轴上,直线BP将△ABC面积分成2:3两部分,求出P点坐标.28. 在 ABC中,∠ABC=90°, ,M是BC上一点,连接AM.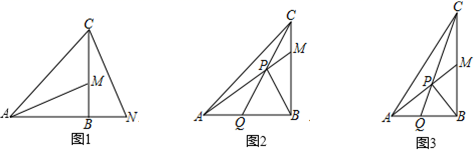 (1)、如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN.(2)、过点B作BP⊥AM,P为垂足,连接CP并延长交AB于点Q.
(1)、如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN.(2)、过点B作BP⊥AM,P为垂足,连接CP并延长交AB于点Q.①如图2,若n=1,求证: .
②如图3,若M是BC的中点,求tan∠BPQ的值.(用含n的式子表示)
29. 如图1,四边形ABCD是正方形,且AB=8,点O与B重合,以O为圆心,作半径长为5的半圆O,交BC于E,交AB于F,交AB延长线于G点,M是半圆O上任一点; (1)、AM的最大值为 , S阴影= .(2)、如图2,将半圆O绕点F逆时针旋转,旋转角为α(0°<α<180°).
(1)、AM的最大值为 , S阴影= .(2)、如图2,将半圆O绕点F逆时针旋转,旋转角为α(0°<α<180°).①若点C落在半圆O的直径GF上,求圆心O到AB的距离;
②若α=90°,求半圆O落在正方形内部的弧长;
(3)、在旋转过程中,若半圆O与正方形的边相切,求点A到切点的距离.(注:sin37°= ,sin53°= ,tan37°= )
30. 如图,在Rt△ABC中,∠ACB=90°,D为BC上一点,以AD为直径的⊙O经过点C,交AB于点E,且AC=AE,CF为⊙O的直径,连接FE并延长交BC于点G,连接AF。 (1)、求证:四边形ADGF是平行四边形;(2)、若AF:BC=3:8,BE=4,求⊙O的直径。
(1)、求证:四边形ADGF是平行四边形;(2)、若AF:BC=3:8,BE=4,求⊙O的直径。