初中数学浙教版八年级上册期末复习专题：一次函数

试卷更新日期：2021-12-23 类型：复习试卷

进入出卷网下载

一、单选题

1. 一次函数 $y = 3 x + 2$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在平面直角坐标系中，一次函数 $y = k x + 3 (k \neq 0)$ 的图象经过点 $P (5 ， 13)$ ，则这个一次函数的表达式是（）

A、 $y = - 2 x + 3$ B、 $y = \frac{16}{5} x + 3$ C、 $y = 2 x + 3$ D、 $y = x + 3$

查看试题解析
3. 在平面直角坐标系中，若点 $(x_{1} ， - 1)$ ， $(x_{2} ， - 2)$ ， $(x_{3} ， 1)$ 都在直线 $y = - 2 x + b$ 上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} > x_{2} > x_{3}$ B、 $x_{3} > x_{2} > x_{1}$ C、 $x_{2} > x_{1} > x_{3}$ D、 $x_{2} > x_{3} > x_{1}$

查看试题解析
4. 已知一次函数y=（a+1）x+b的图象如图所示，那么a的取值范围是（）

A、 $a > 1$ B、 $a < - 1$ C、 $a > - 1$ D、 $a < 0$

查看试题解析
5. 一次函数y＝（k+3）x+b（k＞0，b＜0）在平面直角坐标系中的图象大致是（　　）

A、 B、 C、 D、

查看试题解析
6. 如图，在平面直角坐标系中，点 $A (3 ， m)$ 在第一象限，若点 $A$ 关于 $x$ 轴的对称点 $B$ 在直线 $y = - x + 1$ 上，则 $m$ 的值为（）

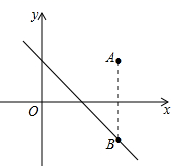A、-1 B、1 C、2 D、3

查看试题解析

7. 漏刻是我国古代的一种计时工具．据史书记载，西周时期就已经出现了漏刻，这是中国古代人民对函数思想的创造性应用．小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型，研究中发现水位h（cm）是时间t（min）的一次函数，如下表是小明记录的部分数据，其中有一个h的值记录错误，错误的h的值为（）

t（min）	…	1	2	3	4	…
h（cm）	…	2.4	2.8	3.4	4	…

A、2.4 B、2.8 C、3.4 D、4

查看试题解析

8. 将一次函数y＝﹣3x的图象沿y轴向下平移4个单位长度后，所得图象的函数表达式为（　　）

A、y＝﹣3（x﹣4） B、y＝﹣3x+4 C、y＝﹣3（x+4） D、y＝﹣3x﹣4

查看试题解析
9. 小华和小明是同班同学，也是邻居，某日早晨，小明7：40先出发去学校，走了一段后，在途中停下吃了早餐，后来发现上学时间快到了，就跑步到学校；小华离家后直接乘公共汽车到了学校，如图是他们从家到学校已走的路程 $S$ （米）和所用时间 $t$ （分钟）的关系图，则下列说法中错误的是（）

A、小明家和学校距离1200米 B、小华乘公共汽车的速度是240米/分 C、小华乘坐公共汽车后7：50与小明相遇 D、小明从家到学校的平均速度为80米/分

查看试题解析
10. 已知一次函数 $y_{1} = a x + b$ 和 $y_{2} = b x + a$ $(a \neq b)$ ，函数 $y_{1}$ 和 $y_{2}$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析

11. 变量x ， y的一些对应值如表：

x	…	﹣2	﹣1	0	1	2	3	…
y	…	4	2	0	﹣2	﹣4	﹣6	…

根据表格中的数据规律，当x＝11时，y的值是（）

A、﹣22 B、﹣11 C、11 D、22

查看试题解析

12. 将直线 $y = - 2 x - 1$ 向下平移两个单位，平移后的直线所对应的函数关系式为（）

A、 $y = - 2 x - 5$ B、 $y = - 2 x - 3$ C、 $y = - 2 x + 1$ D、 $y = - 2 x + 3$

查看试题解析
13. 点 $A (x_{1} ， y_{1})$ 、点 $B (x_{2} ， y_{2})$ 在正比例函数 $y = - 4 x$ 的图像上，当 $x_{1} < x_{2}$ 时，则 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} > y_{2}$ C、 $y_{1} = y_{2}$ D、无法判断

查看试题解析

二、填空题

14. 函数 $y = \frac{k}{x}$ 中，自变量x的取值范围是．

查看试题解析

15. 二次函数y＝ax＋bx＋c的部分对应值如表：

x	…	﹣3	﹣2	0	1	3	5	…
y	…	7	0	﹣8	﹣9	﹣5	7	…

当x＝﹣1时，对应的函数值y ．

查看试题解析

16. 如图所示，在三角形 $A B C$ 中，已知 $B C = 16$ ，高 $A D = 10$ ，动点 $Q$ 由点 $C$ 沿 $C B$ 向点 $B$ 移动 $($ 不与点 $B$ 重合 $) .$ 设 $C Q$ 的长为 $x$ ，三角形 $A C Q$ 的面积为 $S$ ，则 $S$ 与 $x$ 之间的关系式为．

查看试题解析
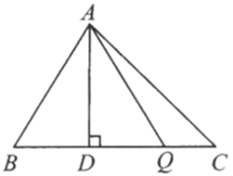17. 山西近期遭遇严重洪涝灾害，1.7万余间房屋倒塌．下图是汾河沿线某个村庄的受灾情况和蓝天救援队的排涝现场．某地需排水约 $50 m^{3}$ ，打开排水泵开始排水，排走的水量与排水时间的关系如下表所示．排水12分钟后，剩下水量为 $m^{3}$ ．

排水时间/分钟

1

2

3

4

…

剩下的水量/ $m^{3}$

48

46

44

42

…

查看试题解析
18. 已知k、b是一元二次方程 $(x + 1) (x - 1) = 0$ 的两个根，且 $k > b$ ，则函数 $y = k x + b$ 的图像不经过第象限．

查看试题解析
19. 某地出租车计费方法如图所示，其中x（单位：km）表示行驶里程，y（单位：元）表示车费．若某乘客一次乘出租车的里程为5km，则这位乘客需支付的费用为元．

查看试题解析
20. 甲乙两人相约从A地到B地，甲骑自行车先行，乙开车，乙到B地后即停车等甲，甲、乙两人之间的距离y（千米）（小时）之间的函数关系如图所示，则乙从A地到B地所用的时间为小时．

查看试题解析
21. 如图，过点A（0，3）的一次函数的图象与正比例函数y＝2x的图象相交于点B ，这个一次函数的表达式是．

查看试题解析

三、综合题

22. 已知动点P以2cm/s的速度沿图1所示的边框从B-C-D-E-F-A的路径运动，记△ABP的面积为S（cm²），S与运动时间t（s）的关系如图2所示，若AB=6cm，请回答下列问题：

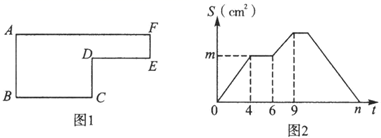(1)、图1中BC= cm，CD= cm，DE= cm；

(2)、求图2中m、n的值．

查看试题解析
23. 将长为 $40 cm$ 、宽为 $15 cm$ 的长方形白纸，按如图所示的方法黏合起来，黏合部分宽为 $5 cm$ ．

(1)、根据图，将表格补充完整：

白纸张数

1

2

3

4

5

$\dots$

纸条长度 $/ cm$

40

110

145

$\dots$

(2)、设 $x$ 张白纸黏合后的总长度为 $y cm$ ，则 $y$ 与 $x$ 之间的关系式是什么？

(3)、你认为白纸黏合起来总长度可能为 $2020 cm$ 吗？为什么？

查看试题解析
24. 长方形的一边长是 $16$ ，其邻边长为 $x$ ，周长是 $y$ ，面积为 $S$ ．

(1)、写出 $x$ 和 $y$ 之间的关系式 $；$

(2)、写出 $x$ 和 $S$ 之间的关系式 $；$

(3)、当 $S = 160$ 时， $x$ 等于多少 $? y$ 等于多少 $?$

(4)、当 $x$ 增加 $2$ 时， $y$ 增加多少 $? S$ 增加多少 $?$

查看试题解析
25. 已知在平面直角坐标系中，直线 $y_{1} = k_{1} x + 4$ （ $k_{1} \neq 0$ ）与直线 $y_{2} = k_{2} x$ （ $k_{2} \neq 0$ ）交于点 $C (6 ， 12)$ ，直线 $y_{1}$ 分别与 $x$ 轴， $y$ 轴交于点 $A$ 和点 $B$ ．

(1)、求直线 $y_{1}$ 与 $y_{2}$ 的表达式及点 $A$ ，点 $B$ 的坐标；

(2)、 $x$ 轴上是否存在点 $P$ ，使 $△ A C P$ 的面积为 $24$ ，若存在，求出点 $P$ 的坐标；若不存在，说明理由；

(3)、点 $P$ 是 $x$ 轴上一动点，过点 $P$ 作 $y$ 轴的平行线交直线 $A C$ 于点 $E$ ，交直线 $O C$ 于点 $F$ ，求出当 $E F$ 长为 $4$ 时点 $P$ 的坐标．（直接写出结果）

查看试题解析
26. 如图，直线y＝kx-6与x轴、y轴分别交于点E、点F ，点E的坐标为（8，0），点A的坐标为（6，0）．

(1)、求一次函数的解析式；

(2)、若点P（x ， y）是线段EF（不与点E、F重合）上的一点，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；

(3)、若点P为直线y＝kx-6上的任意一点，若△OPA的面积为 $\frac{27}{8}$ ，请求出点P的坐标．

查看试题解析
27. 如图，在平面直角坐标系中，直线y= $\frac{1}{2}$ x+1与x轴交于点A，与y轴交于点C，点B （4，3）是直线上的一点．

(1)、求A点和C点的坐标．

(2)、已知x轴上一动点P（m，0），连接BP，若△ABP与△AOC相似，求m的值．

(3)、设直线x= $\frac{5}{3}$ 与BC交于点M，点N是直线x= $\frac{5}{3}$ 上任意一点，且点M 与点N不重合，是否存在点N，使得以M、B、N为顶点的三角形与△AOC相似．若存在，请直接写出N点的坐标；若不存在，请说明理由．

查看试题解析
28. 如图1，在平面直角坐标系中，直线AB： $y = - 3 x + 3$ 分别与y轴、x轴交于AB两点，直线AC交x轴于点C，且满足 $C O = 2 A O$ ．

(1)、求直线AC的表达式；

(2)、如图2，若点P为线段AC上一个动点，过点P作 $P D ⊥ x$ 轴，垂足为D，PD与直线AB交于点Q，当 $△ A P Q$ 的面积等于7时，求点P的坐标；

(3)、如图3，在（2）同的条件下，将 $△ C P D$ 沿x轴向右平移，记平移后的 $△ C P D$ 为 $△ C^{'} P^{'} D^{'}$ ，连接 $A P^{'}$ ， $B P^{'}$ ，当 $△ P^{'} A B$ 为直角三角形时，直接写出点 $P^{'}$ 的坐标．

查看试题解析
29. 已知在平面直角坐标系中，直线 $y_{1} = k_{1} x + 4 (k_{1} \neq 0)$ 与直线 $y_{2} = k_{2} x (k_{2} \neq 0)$ 交于点 $C (6 ， 12)$ ，直线 $y_{1}$ 分别与 $x$ 轴， $y$ 轴交于点 $A$ 和点 $B$ ．

(1)、求直线 $y_{1}$ 与 $y_{2}$ 的表达式及点 $A$ ，点 $B$ 的坐标；

(2)、 $x$ 轴上是否存在点 $P$ ，使 $Δ A C P$ 的面积为 $30$ ，若存在，求出点 $P$ 的坐标；若不存在，说明理由；

(3)、 $x$ 轴上是否存在点 $Q$ ，使 $Δ O C Q$ 为等腰三角形，若存在，请直接写出点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析

排水时间/分钟	1	2	3	4	…
剩下的水量/ $m^{3}$	48	46	44	42	…

白纸张数	1	2	3	4	5	$\dots$
纸条长度 $/ cm$	40		110	145		$\dots$