初数浙教版九上二次函数三种形式和最值问题 专项复习(普通版)
试卷更新日期:2021-12-22 类型:复习试卷
一、单选题
-
1. 二次函数y=(x+1)2+2的最小值是( )A、2 B、1 C、-3 D、32. 在同一平面直角坐标系中,函数 与 的大致图象可能为( )A、
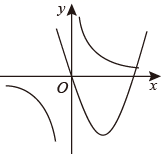 B、
B、 C、
C、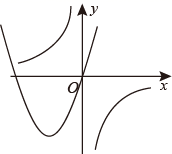 D、
D、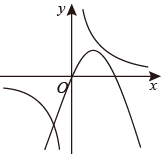 3. 如图,二次函数 图象的对称轴是 ,下列说法正确的是( )
3. 如图,二次函数 图象的对称轴是 ,下列说法正确的是( ) A、 B、 C、 D、4. 将二次函数y= +6x+2化成y= +k的形式应为( )A、y= ﹣7 B、y= +11 C、y= ﹣11 D、y= +45. 已知 的图象如图所示,对称轴为直线 ,若 , 是一元二次方程 的两个根,且 , ,则下列说法正确的是( )
A、 B、 C、 D、4. 将二次函数y= +6x+2化成y= +k的形式应为( )A、y= ﹣7 B、y= +11 C、y= ﹣11 D、y= +45. 已知 的图象如图所示,对称轴为直线 ,若 , 是一元二次方程 的两个根,且 , ,则下列说法正确的是( ) A、 B、 C、 D、6. 如图,已如抛物线 开口向上,与 轴的一个交点为 ,对称轴为直线 .下列结论错误的是( )
A、 B、 C、 D、6. 如图,已如抛物线 开口向上,与 轴的一个交点为 ,对称轴为直线 .下列结论错误的是( )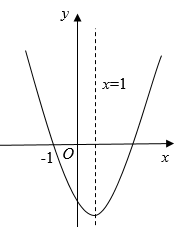 A、 B、 C、 D、7. 二次函数y = ax2-2x-3(a<0)的图象一定不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 在“探索函数 的系数 , , 与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
A、 B、 C、 D、7. 二次函数y = ax2-2x-3(a<0)的图象一定不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 在“探索函数 的系数 , , 与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 二次函数 图像的开口方向是 .10. 二次函数y=﹣(x﹣3)2+6的最大值是 .11. 已知二次函数y=(m-3)x2的图象开口向下,则m的取值范围是12. 如图所示,在同一坐标系中,作出① ;② ;③ 的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号).
 13. 当﹣7≤x≤a时,二次函数y=﹣ (x+3)2+5恰好有最大值3,则a=.14. 如图,二次函数 的函数图象经过点(1,2),且与 轴交点的横坐标分别为 、 ,其中 -1< <0,1< <2,下列结论:① ;② ;③ ;④当 时, ;⑤ ,其中正确的有 .(填写正确的序号)
13. 当﹣7≤x≤a时,二次函数y=﹣ (x+3)2+5恰好有最大值3,则a=.14. 如图,二次函数 的函数图象经过点(1,2),且与 轴交点的横坐标分别为 、 ,其中 -1< <0,1< <2,下列结论:① ;② ;③ ;④当 时, ;⑤ ,其中正确的有 .(填写正确的序号)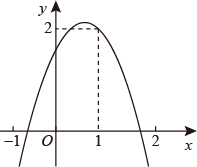 15. 已知抛物线y = ax2+bx-2 (a≠0)的顶点在第三象限,且过点(1, 0),若a-b的值为整数,则b的值为 .16. 出售某种手工艺品,若每个获利x元,一天可售出 个,则当x=元,一天出售该种手工艺品的总利润y最大.
15. 已知抛物线y = ax2+bx-2 (a≠0)的顶点在第三象限,且过点(1, 0),若a-b的值为整数,则b的值为 .16. 出售某种手工艺品,若每个获利x元,一天可售出 个,则当x=元,一天出售该种手工艺品的总利润y最大.三、综合题
-
17. 绿色生态农场生产并销售某种有机产品,每日最多生产130kg,假设生产出的产品能全部售出,每千克的销售价y1(元)与产量x(kg)之间满足一次函数关系y1=﹣ x+168,生产成本y2(元)与产量x(kg)之间的函数图象如图中折线ABC所示.
 (1)、求生产成本y2(元)与产量x(kg)之间的函数关系式;(2)、求日利润为W(元)与产量x(kg)之间的函数关系式;(3)、当产量为多少kg时,这种产品获得的日利润最大?最大日利润为多少元?18. 已知二次函数 的图象经过 两点.(1)、求b的值.(2)、当 时,该函数的图象的顶点的纵坐标的最小值是.(3)、设 是该函数的图象与x轴的一个公共点,当 时,结合函数的图象,直接写出a的取值范围.19. 如图,在平面直角坐标系xOy中,抛物线y=ax2+(2a﹣ma)x﹣2am(a<0)与x轴分别交于点A、C,顶点坐标为D.
(1)、求生产成本y2(元)与产量x(kg)之间的函数关系式;(2)、求日利润为W(元)与产量x(kg)之间的函数关系式;(3)、当产量为多少kg时,这种产品获得的日利润最大?最大日利润为多少元?18. 已知二次函数 的图象经过 两点.(1)、求b的值.(2)、当 时,该函数的图象的顶点的纵坐标的最小值是.(3)、设 是该函数的图象与x轴的一个公共点,当 时,结合函数的图象,直接写出a的取值范围.19. 如图,在平面直角坐标系xOy中,抛物线y=ax2+(2a﹣ma)x﹣2am(a<0)与x轴分别交于点A、C,顶点坐标为D.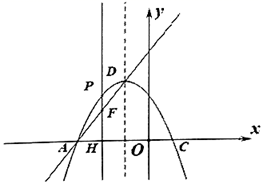 (1)、当a=﹣1,m=1时.
(1)、当a=﹣1,m=1时.①求点D的坐标;
②若F为线段AD上一动点,过点F作FH⊥x轴,垂足为H,交抛物线于点P,当PH+OH的值最大时,求点F的坐标.
(2)、当m= 时,若另一个抛物线y=ax2﹣(6a+ma)x+6am的顶点为E.试判断直线AD是否经过点E?请说明理由.20. 图1中窗户的上部分是由4个全等小正方形组成的大正方形,下部分是矩形,如图2.如果制作一个窗户(如图2)边框的材料总长度为 ,设小正方形的边长为 ,窗户的透光面积为 .
 (1)、求 关于 的函数表达式.(2)、 取何值时,透光面积最大?最大透光面积是多少?21. 某商场将一种每件 成本价为10元的商品连续加价两次后,以每件24元作为定价售出。已知第二次加价的增长率比第一次加价的增长率多10%。(1)、求第一次加价的增长率;(2)、该商场在试销中发现,如果以定价售出,则每天可售出100个。如果销售单价每降低1元,销售量就可以增加10件。那么当销售单价为多少元时,该商场每天销售该商品获得的利润最大?最大利润是多少?
(1)、求 关于 的函数表达式.(2)、 取何值时,透光面积最大?最大透光面积是多少?21. 某商场将一种每件 成本价为10元的商品连续加价两次后,以每件24元作为定价售出。已知第二次加价的增长率比第一次加价的增长率多10%。(1)、求第一次加价的增长率;(2)、该商场在试销中发现,如果以定价售出,则每天可售出100个。如果销售单价每降低1元,销售量就可以增加10件。那么当销售单价为多少元时,该商场每天销售该商品获得的利润最大?最大利润是多少?