福建省南平市浦城县2021-2022学年高一上学期数学期中考试试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 若集合 , , 则( )A、 B、 C、 D、2. 命题的否定是( )A、 B、 C、 D、3. 函数的定义域为( )A、 B、 C、 D、4. 设 , , , 则 , , 的大小关系为( )A、 B、 C、 D、5. 函数 的图象大致为( )A、
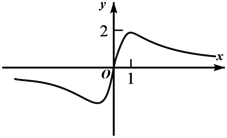 B、
B、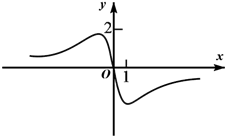 C、
C、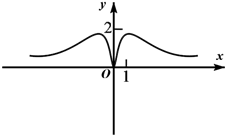 D、
D、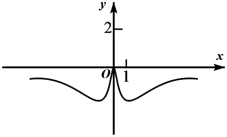 6. 若函数 在区间 上存在零点,则常数a的取值范围为( )A、 B、 C、 D、7. 已知函数y=log2(x2-2kx+k)的值域为R,则k的取值范围是( )A、0<k<1 B、0≤k<1 C、k≤0或k≥1 D、k=0或k≥18. 定义在 上的函数 的图象关于 对称,且 满足:对任意的 , ,且 都有 ,且 ,则关于 的不等式 的解集是( )A、 B、 C、 D、
6. 若函数 在区间 上存在零点,则常数a的取值范围为( )A、 B、 C、 D、7. 已知函数y=log2(x2-2kx+k)的值域为R,则k的取值范围是( )A、0<k<1 B、0≤k<1 C、k≤0或k≥1 D、k=0或k≥18. 定义在 上的函数 的图象关于 对称,且 满足:对任意的 , ,且 都有 ,且 ,则关于 的不等式 的解集是( )A、 B、 C、 D、二、多选题
-
9. 下列函数中,既是偶函数,又在(0,+∞)单调递增的函数是( )A、 B、 C、 D、10. 下列命题正确的是( )A、且; B、且; C、且; D、 .11. 下列四个结论中正确的是( )A、“”是“的函数值恒小于0”的充要条件 B、“ , ”的否定为“ , ” C、函数的值域是 D、函数在上单调递增12. 对于函数 ,则下列判断正确的是( )A、 在定义域内是奇函数 B、函数 的值域是 C、 , ,有 D、对任意 且 ,有
三、填空题
-
13. 函数(且)的图象必过定点.14. 函数的单调递增区间为.15. 若不等式在区间上恒成立,则实数m的取值范围是.16. 已知函数 , 函数 , 若函数恰有4个零点,则实数的取值范围为.
四、解答题
-
17. 求下列各式的值:(1)、;(2)、 .18. 已知 , 不等式的解集是.(1)、求的解析式;(2)、若对于任意 , , 不等式恒成立,求的取值范围.19. 已知集合.集合.
(Ⅰ)当时,求;
(Ⅱ)若 , 求实数的取值范围.
20. 根据试验检测,一辆型运输汽车在高速公路.上匀速行驶时,耗油率(L/h)近似与车速(km/h)的平方成正比,且当车速是100km/h时,耗油率为已知 , 两地间有一条长130km的高速公路,最低限速60km/h,最高限速120km/h.若某环保公司用一辆该型号运输车将垃圾从地转运至地,已知过路费为40元,支付给雇用司机的工资平均每小时80元.假设汽油的价格是8元/L,汽车匀速行驶(起步、必要的减速或提速等忽略不计),问:当行车速度为多少时,转运一次的总费用最低?最低为多少元?