2021-2022学年度第一学期七年级数学第一、二、三章期末综合复习练习卷（人教版）

试卷更新日期：2021-12-22 类型：复习试卷

进入出卷网下载

一、单选题

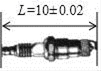
1. 如图，根据某机器零件的设计图纸上信息，判断该零件长度（1）尺寸合格的是（）

A、9.68mm B、9.97mm C、10.1mm D、10.01mm

查看试题解析
2. 解方程， $1 - \frac{x + 3}{6} = \frac{x}{2}$ 利用等式性质去分母正确的是（）

A、 $1 - x - 3 = 3 x$ B、 $6 - x - 3 = 3 x$ C、 $6 - x + 3 = 3 x$ D、 $1 - x + 3 = 3 x$

查看试题解析
3. 太原古县城的打造历时8年，耗资将近300亿元，是太原境内的一个重点工程．它是一个在明代早期修建的古城，很好的传承了“晋阳古城”的文脉，并延续了“晋阳古城”的历史文化．数据300亿元用科学记数法表示为（）

A、 $3 \times 10^{2}$ 元 B、 $3 \times 10^{8}$ 元 C、 $3 \times 10^{10}$ 元 D、 $0.3 \times 10^{10}$ 元

查看试题解析
4. ${(- 4)}^{2}$ 的值为（）

A、 $- 8$ B、8 C、-16 D、16

查看试题解析
5. 若 $x = 1$ 是关于x的方程 $m x - 3 = 2 x$ 的解，则m的值为（）.

A、5 B、-5 C、6 D、-6

查看试题解析
6. 根据美国约翰斯·霍普金斯大学于美国东部时间4月10日18时16分（北京时间4月11日6时16分）统计的数据显示，美国新冠肺炎累计确诊病例已超过3114万例，达到31145168例.将数字3114万用科学记数法表示应为（）

A、 $0.3114 \times 10^{7}$ B、 $3.114 \times 10^{6}$ C、 $3.114 \times 10^{7}$ D、 $31.14 \times 10^{5}$

查看试题解析
7. 河北省某机械厂加工车间有34名工人，平均每名工人每天加工大齿轮20个或小齿轮15个．已知3个大齿轮和2个小齿轮配成一套，问分别安排多少名工人加工大、小齿轮，才能刚好配套？若设加工大齿轮的工人有 $x$ 名，则可列方程为（）

A、 $20 x = 15 (34 - x)$ B、 $2 \times 20 x = 3 \times 15 (34 - x)$ C、 $3 \times 20 x = 2 \times 15 (34 - x)$ D、 $3 \times 20 (34 - x) = 2 \times 15 x$

查看试题解析
8. 已知代数式 $x^{a} y^{2}$ 与 $x y^{2 b}$ 是同类项，则 $a$ 与 $b$ 的值分别是（）

A、 $a = 0$ ， $b = 1$ B、 $a = 2$ ， $b = 1$ C、 $a = 1$ ， $b = 1$ D、 $a = 0$ ， $b = 2$

查看试题解析
9. $2021$ 减去它的 $\frac{1}{2}$ ，再减去余下的 $\frac{1}{3}$ ，再减去余下的 $\frac{1}{4}$ ，....，以此类推，一直减到余下的 $\frac{1}{2021}$ ，则最后剩下的数是（）

A、 $0$ B、 $1$ C、 $\frac{2020}{2021}$ D、 $\frac{2021}{2020}$

查看试题解析
10. 已知0≤a≤4，那么|a﹣2|＋|3﹣a|的最大值等于（）

A、1 B、5 C、8 D、3

查看试题解析

二、填空题

11. 将3210000用科学记数法表示为．

查看试题解析
12. 计算 $5 a^{2} + 2 a^{2}$ 的结果等于．

查看试题解析
13. 若 $- \frac{1}{2} y^{2} x^{m}$ 与5x³y²ⁿ是同类项，则m+n＝.

查看试题解析
14. 某同学计划在假期每天做6道数学题，超过的题数记为正数，不足的题数记为负数，十天中做题记录如下：-3，5，-4，2，-1，1，0，-3，8，7，那么他十天共做的数学题有道．

查看试题解析
15. 同学们都知道： $| 5 - (- 2) |$ 表示5与-2之差的绝对值，实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离，同理， $| x + 2 | + | x - 3 |$ 可以表示数轴上有理数x所对应的点到-2和3所对应的点的距离之和，则 $| x + 3 | + | x - 2 |$ 的最小值为.

查看试题解析

三、计算题

16. 化简

(1)、 $5 x y - 2 y^{2} - 3 x y - 4 y^{2}$

(2)、 $2 (2 a - 3 b) - 3 (2 b - 3 a)$

查看试题解析
17. 合并同类项：

(1)、 $5 m + 2 n - m - 3 n$

(2)、 $3 a^{2} - 1 - 2 a - 5 + 3 a - a^{2}$

查看试题解析

四、解答题

18. 小明在对方程 $\frac{2 x - 1}{3} + 1 = \frac{x + a}{2}$ 去分母时，方程左边的 $1$ 没有乘以 $6$ ，因而求得的解是 $x = 4$ ，试求 $a$ 的值，并求出方程的正确解.

查看试题解析
19. 某牛奶厂现有鲜奶9吨，若在市场上直接销售鲜奶，每吨可获取利润500元；若制成酸奶销售，每吨可获取利润1200元；若制成奶片销售，每吨可获取利润2000元.该工厂的生产能力是，如果制成酸奶，每天可加工3吨；制成奶片，每天可加工1吨，受人员限制，两种加工方式不可同时进行；受气温限制这批牛奶必须4天内全部销售或加工完毕.为此该厂设计了三种方案：
方案一：将鲜奶全部制成酸奶销售；

方案二：尽可能地制成奶片，其余的直接销售鲜奶；

方案三：将一部分制成奶片，其余的制成酸奶销售，并恰好4天完成.

你认为选择哪种方案获利最多？

查看试题解析
20. 先化简，再求值：
$5 x^{2} - [2 x y - 3 (\frac{1}{3} x y + 2) + 5 x^{2}$ 其中 $| 2 x - 1 | + {(3 y + 2)}^{2} = 0$

查看试题解析
21. 某同学在计算一个多项式减去 $2 x^{2} - 4 x + 5$ 时，误认为加上此式，计算出的错误结果为 $- 2 x^{2} + x - 1$ ，试求出这个多项式，并求出正确结果．

查看试题解析
22. 2021年！1月1日，某社区接种新冠疫苗第二针(分为北京科兴和北京生物两种)人数共110人，其中接种北京科兴的人数是接种北京生物的人数的2倍多20人，求接种两种疫苗的人数分别是多少人？

查看试题解析