浙江省温州市瑞安市2021-2022学年八年级上学期数学12月双减作业反馈检测试卷

试卷更新日期：2021-12-22 类型：月考试卷

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分．)

1. 下列长度的三条线段，能首尾相连围成三角形的是（）

A、1cm，2cm，3cm B、2cm，3cm，4cm C、1cm，1cm，2cm D、1cm，2cm，4cm

查看试题解析
2. 下图是设计师石昌鸿设计的《魅力中国》部分城市字体，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在平面直角坐标系中，点P(-3，2)所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 不等式3x+4 $\geq$ 1的解集是（）

A、 B、 C、 D、

查看试题解析
5. 已知点M(m+1，1-m)在y轴上，则点M的坐标是（）

A、(2，0) B、(-2，0) C、(0，-2) D、(0，2)

查看试题解析
6. 下列选项中，可以用来证明命题“若x² $>$ 9，则x $>$ 3”是假命题的反例是（）

A、x $=$ 3 B、x $=$ -3 C、x $=$ 4 D、x $=$ -4

查看试题解析
7. 如图，这是某所学校的部分平面示意图，教学楼、实验楼和图书馆的位置都在边长为1的小正方形网格线的交点处，若教学楼位置的坐标是( $-$ 2，2)，实验楼位置的坐标是(2， $-$ 1)，则图书馆位置的坐标是（）

A、(4，1) B、(1，4) C、(3，2) D、(2，3)

查看试题解析
8. 如图，在△ABC和△BAD中，已知∠CAB=∠DBA，添加下列条件，还不一定能判定△ABC≌△BAD的是（）

A、∠C=∠D B、AC=BD C、BC=AD D、AM=BM

查看试题解析
9. 在平面直角坐标系中，将点A(a，1-a)先向左平移3个单位得点A₁ ，再将A₁向上平移1个单位得点A₂ ，若点A₂落在第三象限，则a的取值范围是（）

A、2 $< a <$ 3 B、a $<$ 3 C、a $>$ 2 D、a $<$ 2或a $>$ 3

查看试题解析
10. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示．连结AE，若大正方形ABCD的面积为169，△ABE的面积为72，则小正方形EFGH的面积是（）

A、36 B、49 C、48 D、50

查看试题解析

二、填空题(本题有6小题，每小题3分，共18分)

11. 点( $-$ 1，3)关于x轴对称点的坐标是．

查看试题解析
12. 不等式组 ${\begin{cases} x - 1 > 0 \\ 2 x < 6 \end{cases}$ 的整数解是．

查看试题解析
13. 如图，在等边三角形ABC中，CD⊥AB于点D，若AB=2，则CD的长是．

查看试题解析
14. 某电梯的额定限载量为1000千克，某人要用电梯把一批重物从底层搬到顶层，若人的身体质量为70千克，每箱货物质量为30千克，问他每次最多搬运多少箱？若设每次搬运货物x箱，则根据题意可列出关于x的不等式：．

查看试题解析
15. 如图，在Rt△ABC中，∠A $=$ 90°，∠B $=$ 38°，点E，F分别在边BC，AC上，将△CEF沿EF所在的直线折叠，使C的对应点 $C^{'}$ 落在AB上，且 $C^{'}$ E=B $C^{'}$ ，则∠AF $C^{'}$ = ．

查看试题解析
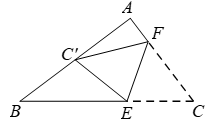16. 某校八年级数学兴趣小组活动，准备将一块底为10cm，高为12.8cm的三角形纸板分割成四块(如图1)，然后将这四块拼成一张正方形纸板(无缝隙不重叠，如图2)，则DG 的长是cm，CF的长是cm．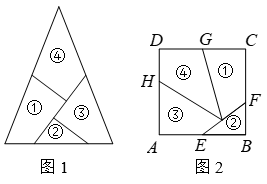

查看试题解析

三、解答题(本题有7小题，共52分．)

17.

(1)、解不等式： $3 x - 1 > x + 3$

(2)、解不等式组 ${\begin{cases} 5 x - 2 < 3 \\ 2 (x - 1) > x - 3 \end{cases}$

查看试题解析
18. 已知：如图，在△ADF和△BCE中，点B，F，E，D依次在一条直线上，若AF∥CE，∠B $=$ ∠D ，BF $=$ DE，求证：AF $=$ CE．

查看试题解析
19. 如图，在10×10的方格纸中，建立如图所示的直角坐标系，每个小正方形的边长为1，△ABC的顶点都在格点上．

⑴将△ABC向下平移3个单位得到△A₁B₁C₁ ，请在图中画出△A₁B₁C₁ ．

⑵请在图中画出△ABC关于y轴对称的△A₂B₂C₂ ．

查看试题解析
20. 如图，在平面直角坐标系中，点A( $-$ 1， $-$ 2) ，B(5， $-$ 2) ．点C(2a +1，2 $-$ a) 在第一象限内，过点C作直线CD∥AB，交y轴于点D．

(1)、若AB= $\frac{3}{2}$ CD，求点C的坐标．

(2)、若△ABC的面积为9，求△ABC的周长．

查看试题解析
21. 如图，在△ABC中，AB=AC，CD⊥AB于点D，过点D作DE⊥BC于点E，交CA的延长线于点F．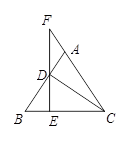

(1)、求证：△ADF是等腰三角形．

(2)、当CD $=$ 8，CF=10时，求BD的长．

查看试题解析
22. 每年11月份脐橙和蜜桔进入销售旺季．某水果专销商购进脐橙和蜜桔共1000箱．设购进蜜桔x箱，这两种水果的售价与进价如下表所示：

品种

售价(元/箱)

进价(元/箱)

蜜桔

28

20

脐橙

31

25

(1)、请用含x的代数式表示该商家售完这1000箱水果所获得的利润．

(2)、为了迎接“双11”活动，商家决定进行组合促销活动：两种水果各一箱打包成一组，售价为55元/组，其组数为购进蜜桔箱数的 $\frac{1}{5}$ ，未打包的按原价出售．若这两种水果全部卖出，利润不少于6500元，则该商家至少要购进蜜桔多少箱？

查看试题解析
23. 如图，在平面直角坐标系中，点A(-4，0)，C(3，0)，D(0，4)， AG⊥CD于点G，交y轴于点B.

(1)、求证：△AOB≌△DOC．

(2)、点E在线段AB上，作OF⊥OE交CD于点F，连结EF．
①若E是AB的中点，求△OEF的面积.

②连结DE，当△DEF是以DE为腰的等腰三角形时，求CF的长．

查看试题解析

品种	售价(元/箱)	进价(元/箱)
蜜桔	28	20
脐橙	31	25