重庆市长寿区2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点M（3，－5）关于原点对称的点的坐标是（）

A、（－3，－5） B、（3，5） C、（5，－3） D、（－3，5）

查看试题解析
3. 袋子中装有4个黑球和2个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球，下列事件是必然事件的是（　　）

A、摸出的三个球中至少有一个球是黑球 B、摸出的三个球中至少有一个球是白球 C、摸出的三个球中至少有两个球是黑球 D、摸出的三个球中至少有两个球是白球

查看试题解析
4. 若直线 $a$ 与半径为4的⊙O相交，则圆心O到直线 $a$ 的距离可能为（）

A、3 B、4 C、4.5 D、5

查看试题解析
5. 若关于x的一元二次方程x²﹣2x+m=0有两个不相等的实数根，则m的取值范围是（）

A、m＜﹣1 B、m＜1 C、m＞﹣1 D、m＞1

查看试题解析
6. 某校学生小明每天上学时都要经过一个十字路口，该十字路口有红、黄、绿三色交通信号灯，他在路口遇到红灯的概率为 $\frac{1}{3}$ ，遇到黄灯的概率为 $\frac{1}{9}$ ，那么他遇到绿灯的概率为（　　）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{4}{9}$ D、 $\frac{5}{9}$

查看试题解析
7. 如图，△ABC是⊙O的内接三角形，∠OAB=35°，则∠ACB的度数为（）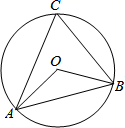

A、35° B、55° C、60° D、70°

查看试题解析
8.
如图，在Rt△ABC中，∠C = 90°，∠B = 30°，BC =" 4" cm，以点C为圆心，以2 cm的长为半径作圆，则⊙C与AB的位置关系是（）．

A、相离 B、相切 C、相交 D、相切或相交

查看试题解析
9. 如图，在 $△$ ABC中，∠ACB＝90°，∠A＝30°，BC＝4，将 $△$ ABC绕点C按顺时针方向旋转 $n$ °后，得到 $△$ EDC，此时，点D在AB边上，斜边DE交AC边于点F，则 $n$ 的大小，图中阴影部分的面积分别为（）

A、30，4 B、60，4 C、60， $2 \sqrt{3}$ D、60， $4 \sqrt{3}$

查看试题解析
10. 将抛物线y=x²+1先向左平移2个单位，再向下平移3个单位，那么所得抛物线的函数关系式是（　　）

A、y＝(x＋2)²＋2 B、y＝(x＋2)²－2 C、y＝(x－2)²＋2 D、y＝(x－2)²－2

查看试题解析
11. 在同一直角坐标系中，函数y=kx²﹣k和y=kx+k（k≠0）的图象大致是（　　）

A、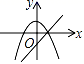 B、 C、 D、

查看试题解析
12. 如果关于 $x$ 的方程 $\frac{1}{2 - x} - 2 = \frac{1 - m x}{x - 2}$ 有正数解，且关于 $x$ 的方程 $m x^{2} - 2 \sqrt{2} x - 1 = 0$ 有两个不相等的实数根，则符合条件的整数 $m$ 的值是（）

A、-1 B、0 C、1 D、-1或1

查看试题解析

二、填空题

13. 如图，将△ABC绕着点C顺时针旋转50°后得到△A’B’C.若 $∠ A$ =40°， $∠ B'$ =110°，则∠ $B C A^{'}$ 的度数为.

查看试题解析
14. 已知⊙O的内接正六边形的周长为18 cm，则这个圆的半径是cm.

查看试题解析
15. 已知x=1是一元二次方程 $x^{2} + m x + n = 0$ 的一个根，则 $m^{2} + 2 m n + n^{2}$ 的值为.

查看试题解析
16. 从 $- 2$ ，0， $2$ 这三个数中，任取两个不同的数分别作为 $a$ ， $b$ 的值，恰好使得关于 $x$ 的方程 $x^{2} + a x - b = 0$ 有实数解的概率为.

查看试题解析
17. 如图，AB是 $⊙ O$ 的直径，弦CD交AB于点 $E$ ，且 $E$ 为OB的中点∠CDB=30°，CD=6 $\sqrt{3}$ ，则阴影部分的面积为.

查看试题解析
18. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图所示对称轴为x＝﹣ $\frac{1}{2}$ .下列结论中：
①abc＞0；②a+b＝0；③2b+c＞0；④4a+c＜2b.

正确的有（只要求填写正确命题的序号）

查看试题解析

三、解答题

19. 已知：关于x的方程x²+2mx+m²-1=0

(1)、不解方程，判别方程根的情况；

(2)、若方程有一个根为3，求m的值．

查看试题解析
20. 已知正实数 $m$ 满足 $\frac{4 - m}{m^{2} + 1} = 1$ ，求代数式 $(\frac{2 m - 1}{m + 1} - m + 1) \div \frac{m - 2}{m + 1}$ 的值.

查看试题解析
21. 八年级（1）班学生在完成课题学习“体质健康测试中的数据分析”后，利用课外活动时间积极参加体育锻炼，每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练，训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.

请你根据上面提供的信息回答下列问题：

(1)、扇形图中跳绳部分的扇形圆心角为度，该班共有学生人，训练后篮球定时定点投篮平均每个人的进球数是.

(2)、老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试，请用列表或画树形图的方法求恰好选中两名男生的概率.

查看试题解析
22. 设 $b$ 为常数，已知二次函数 $y = - 2 x^{2} - 2 b x + b^{2} + 1$ .

(1)、求证：无论 $b$ 为何值，该二次函数的图象与 $x$ 轴一定有两个不同的交点；

(2)、若把二次函数的图象沿 $y$ 轴方向平移 $2$ 个单位长度，则使得该二次函数的图象与 $x$ 轴恰有一个公共点，求 $b$ 的值.

查看试题解析
23. 某商场经营一种新型台灯，进价为每盏300元.市场调研表明：当销售单价定为400元时，平均每月能销售300盏；而当销售单价每下降1元时，平均每月的销售量就增加10盏.

(1)、当销售单价为多少时，该型台灯的销售利润平均每月能达到40000元？

(2)、临近春节，为了回馈广大顾客，商场部门经理决定在一月份开展降价促销活动，估计分析：若每盏台灯的销售单价在（1）的最高销售单价基础上降价 $m$ %，则可多售出2 $m$ %.要想使一月份的销售额达到209950元，并且保证不亏损，求 $m$ 的值.

查看试题解析
24. 如图，AB是⊙O的直径，P在AB的延长线上，PD与⊙O相切于D，C在⊙O上，PC＝PD.

(1)、求证：PC是⊙O的切线.

(2)、连接AC，若AC＝PC，PB＝1，求⊙O的半径.

查看试题解析
25. 如图，对称轴为直线 $x = - 1$ 的二次函数 $y = - x^{2} + b x + c$ 的图象与x轴交于A、B两点，与y轴交于C点，B点的坐标为(1，0).

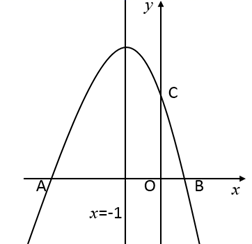(1)、求此二次函数的解析式；

(2)、在直线 $x = - 1$ 上找一点P，使 $△$ PBC的周长最小，并求出点P的坐标；

(3)、若第二象限的且横坐标为t的点Q在此二次函数的图象上，则当t为何值时，四边形AQCB的面积最大？最大面积是多少？

查看试题解析
26. 如图，在正方形ABCD中，点E是BC边延长线上的任意一点，AE交CD于点G，△AEB绕点E逆时针旋转后点B的对应点B′落在AE上，另一边E $A^{'}$ 交CD的延长线于点F.

(1)、如图1，若正方形ABCD的边长为1，∠AEB＝30°，求线段DF的长；

(2)、如图2，若点G是CD的中点时，过点G作GH⊥AF于点H.求证： $2 \sqrt{2}$ DH＝CE；

(3)、如图3，若点G是CD的中点时，试探究CE、EF、AF有怎样的数量关系？直接写出结果.

查看试题解析