重庆市万州区2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. -2020的绝对值是（）

A、-2020 B、2020 C、 $- \frac{1}{2020}$ D、 $\frac{1}{2020}$

查看试题解析
2. 下列立体图形的主视图为圆形的是（）

A、 B、 C、 D、

查看试题解析
3. 计算 ${(a^{2} b)}^{3}$ 的结果正确的是（）

A、 $3 a^{2} b$ B、 $a^{6} b$ C、 $a^{6} b^{3}$ D、 $a^{2} b^{3}$

查看试题解析
4. 若 $a - b = 2$ ，则代数式 $- 2 a + 2 b - 3$ 的值为（）

A、-7 B、-1 C、1 D、7

查看试题解析
5. 如图，若点A、O、B在一条直线上， $O M$ 平分 $∠ A O C$ ， $∠ B O N ： ∠ C O N = 1 ： 4$ ，当 $∠ A O M = 20 °$ 时，则 $∠ B O N =$ （）

A、 $112 °$ B、 $70 °$ C、 $28 °$ D、 $20 °$

查看试题解析
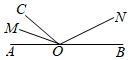6. 估计 $\sqrt{75} - 2 \sqrt{3}$ 的值应在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
7. 某商店把一商品按标价的九折出售（即优惠10%），仍可获利20%，若该商品的标价为每件28元，则该商品的进价为（　　）

A、21元 B、19.8元 C、22.4元 D、25.2元

查看试题解析
8. 如图是由同样大小的棋子按照一定规律组成的图形，其中第①个图中需要8枚棋子，第②个图中需要17枚棋子，第③个图中需要26枚棋子，第④个图中需要有35枚棋子……照此规律排列下去，则第⑩个图中需要的棋子枚数为（）

A、79 B、89 C、99 D、109

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 13$ ， $B C = 12$ ，D为 $B C$ 边上一点，将 $△ A B D$ 沿 $A D$ 折叠，若点B恰好落在线段 $A C$ 的延长线上点E处，则 $D E$ 的长为（）

A、 $\frac{12}{5}$ B、 $\frac{26}{5}$ C、 $\frac{26}{3}$ D、 $\frac{34}{3}$

查看试题解析
10. 要使关于x的分式方程 $\frac{a}{x} = 1 - \frac{a}{2 x}$ 有整数解，且使关于x的不等式组 ${\begin{array}{l} x \geq - 2 \\ 5 x < a \end{array}$ 恰好有两个整数解，则满足条件a的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
11. 如图， $E F$ 是垂直于水平面的一棵大树，小莹同学在A点处目测大树顶端F的仰角约为 $31 °$ ，然后她沿一段坡度 $i = 4 ： 3$ ，坡长为5米的斜坡 $A B$ 到达B点，再沿水平方向向右行走2米到达C点（A、B、C、E、F在同一平面内），在C处目测得大树的顶端F的仰角约为 $37 °$ ，已知小莹同学的身高为1.6米，则大树 $E F$ 的高度约为（）米（参考数据： $\tan 31 ° \approx 0.60$ ， $\sin 31 ° \approx 0.52$ ， $\tan 37 ° \approx 0.75$ ， $\sin 37 ° \approx 0.60$ ）.

A、31.6米 B、34.6米 C、35.6米 D、36.6米

查看试题解析
12. 如图，反比例函数 $y = \frac{28}{x} (x > 0)$ 的图象经过正方形 $A B C D$ 的顶点D，反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象经过正方形 $A B C D$ 的顶点A和顶点B， $A D$ 边交y轴于点E，若 $\frac{A E}{D E} = \frac{1}{2}$ ，且顶点C的纵坐标为1，则k的值为（）

A、-18 B、-20 C、-21 D、-24

查看试题解析

二、填空题

13. 第六次全口人数普查数据显示，万州全区常住人口超1650000人，数据1650000用科学记数法表示为.

查看试题解析
14. 已知 $△ A O B$ 与 $△ C O D$ 是位似图形，位似中心为点O，若 $O A ： O C = 1 ： 3$ ，则 $△ A O B$ 与 $△ C O D$ 的面积之比为.

查看试题解析
15. 小王和小李同学在一次数学能力测试中，对一道单项选择题一点思路都没有，该选择题设有A、B、C、D四个选项，则他们都猜对的概率为.

查看试题解析
16. 如图，在平行四边形 $A B C D$ 中E、F分别是边 $A D$ 、 $B C$ 上一点， $D E = B F$ ，连接 $A C 、 E F 、 A F 、 C E$ ，若 $A E = A F ， A C = 5 ， E F = 8$ ，则四边形 $A E C F$ 的面积为.

查看试题解析
17. 周末，张琪和爸爸一同前往万达广场玩耍，但中途爸爸有事需立刻返回，而张琪保持原速继续前行5分钟后，觉得一个人到万达广场也不好玩，于是她也立刻沿原路返回，结果两人恰好同时到家.张琪和爸爸在整个运动过程中离家的路程 $y_{1}$ （米）、 $y_{2}$ （米）与运动时间x（分）之间的函数关系如图所示，求张琪开始返回时与爸爸相距米.

查看试题解析
18. 三兄弟带着西瓜到农贸市场去卖：老大带了10个，老二带了16个，老三带了26个.上午他们按同一价格卖了若干个西瓜（西瓜按个数出售），过了中午，怕西瓜卖不完，他们跌价把所有的西瓜仍按同一价格全部卖掉了，回家后，他们清点卖瓜款后发现，三人卖瓜所得的款一样多，m表示老大上午与老三上午卖的西瓜个数之差，n表示老二上午与老三上午卖的西瓜个数之差，则 $\frac{m}{n} =$ .

查看试题解析

三、解答题

19. 计算：

(1)、 ${(2 x - y)}^{2} - y (2 x + y)$

(2)、 $\frac{x^{2} + 6 x + 9}{x - 2} \div (x + 2 + \frac{3 x + 4}{x - 2})$

查看试题解析
20. 如图，在矩形 $A B C D$ 中， $∠ B A D$ 的平分线交 $B C$ 于点E，交 $D C$ 的延长线于点F.

(1)、若 $A B = 2$ ， $A D = 3$ ，求 $E F$ 的长；

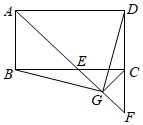(2)、若G是 $E F$ 的中点，连接 $B G$ 和 $D G$ ，求证： $△ B C G ≌ △ D F G$ .

查看试题解析

21. 某校组织学生参加“防疫卫生知识竞赛”（满分为100分）.竞赛结束后，现从七年级、八年级各随机抽取20名学生的竞赛成绩（百分制）进行分析，过程如下：

七年级：89，95，85，92，85，86，97，80，85，100，85，89，91，83，85，90，94，69，93，87.

八年级：10，91，97，92，82，91，100，93，87，93，90，91，84，91，72，87，92，90，80，57.

整理数据：分析数据：

	$50 \leq x \leq 59$	$60 \leq x \leq 69$	$70 \leq x \leq 79$	$80 \leq x \leq 89$	$90 \leq x \leq 100$
七年级	0	1	0	a	8
八年级	1	0	1	5	13

应用数据：

	平均数	众数	中位数
七年级	88	85	b
八年级	88	c	91

(1)、由上表填空：

a =

，

b =

，

c =

(2)、若该校七、八两个年级共有学生2400人，请你估计两个年级在本次竞赛中成绩高于95分的共有多少人？

(3)、你认为哪个年级的学生对防疫卫生知识掌握的总体水平较好，请说明理由.

查看试题解析

22. 阅读下列材料：
定义：对于一个两位数x，如果x满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“相异数”，将一个“相异数”的个位数字与十位数字对调后得到一个新的两位数，将这个新的两位数与原两位数求和，再同除以11所得的商记为 $S (x)$ .

例如， $a = 13$ ，对调个位数字与十位数字得到的新两位数31，新两位数与原两位数的和为 $13 + 31 = 44$ ，和44除以11的商为 $44 \div 11 = 4$ ，所以 $S (13) = 4$ .

(1)、若一个“相异数”y的十位数字是k，个位数字是 $2 (k - 1)$ ，且 $S (y) = 10$ ，求相异数y；

(2)、若一个两位数x是“相异数”，且 $S (x) = 8$ ，求满足条件的x的个数.

查看试题解析

23. 有这样一个问题：探究函数

y = \frac{\sqrt{x + 2}}{x}

的图象与性质.小华根据学习函数的经验，对函数

y = \frac{\sqrt{x + 2}}{x}

图象与性质进行了探究.下面是小华的探究过程，请补充完整：

如表是y与x的几组对应值.

x	$- 2$	$- \frac{3}{2}$	-1	$- \frac{1}{2}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	4	…
y	0	$- \frac{\sqrt{2}}{3}$	m	$- \sqrt{6}$	$\sqrt{21}$	$\sqrt{10}$	$\sqrt{3}$	1	$\frac{\sqrt{5}}{3}$	$\frac{\sqrt{6}}{4}$	…

(1)、m的值为；

(2)、如图，在平面直角坐标系

x o y

中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象；

(3)、结合函数的图象，判断下列关于该函数性质结论正确的是.

①函数关于原点对称；

②在每个象限内，函数y随x的增大而减小；

③当 $x = - 2$ 时，函数有最大值0；

(4)、结合函数图象估计

\frac{\sqrt{x + 2}}{x} - x - 4 = 0

的解的个数为个.

查看试题解析

24. 每年的“双十二”接近寒冬，各商家抓住这一季节交替之际，许多商家利用这一契机进行了打折销售活动.某淘宝网店推出了甲、乙两款取暖器，已知甲款取暖器每台的进价为40元，标价为60元；乙款取暖器每台的进价为120元，标价为160元.

(1)、若该网店在去年“双十二”当天按标价销售，共卖了200台甲、乙两款取暖器，结果发现利润不低于6400元，求乙款取暖器至少卖了多少台？

(2)、现在正值销售旺季，为减少乙款取暖器的库存，该网店决定今年的“双十二”当天进行促销活动.甲款取暖器的售价每台在标价的基础上提高 $\frac{1}{4} m %$ ，乙款取暖器售价每台在标价的基础上降低 $\frac{3}{8} m %$ ，在实际销售过程中甲款取暖器销售量比（1）中的甲款最多销售量增加了 $m %$ ；乙款取暖器销售量比（1）中的乙款最少销售量增加了 $2 m %$ ，最终乙款取暖器的销售额是甲款取暖器的销售额4倍，求m的值.

查看试题解析
25. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴相交于点 $A (- 1 ， 0)$ 和点B，交y轴于点C， $C O = 3 A O$ ，点P是抛物线上第一象限内的一动点.

(1)、求抛物线的解析式；

(2)、过点P作 $P D / / y$ 轴交 $B C$ 于点D，求线段 $P D$ 长度的最大值；

(3)、若Q为坐标平面内一点，在（2）的条件下，是否存在点Q，使得以点P、C、D、Q为顶点的四边形为平行四边形，若存在，请直接写出点Q的坐标；若不存在，请说明理由.

查看试题解析
26. 在菱形 $A B C D$ 中， $A B = 4$ ， $∠ A B C = 60 °$ ，E是对角线 $A C$ 上一点，F是线段 $B C$ 延长线上一点，且 $C F = A E$ ，连接 $B E$ 、 $E F$ .

(1)、如图1，若E是线段 $A C$ 的中点，求 $E F$ 的长；

(2)、如图2，若E是线段 $A C$ 延长线上的任意一点，求证： $B E = E F$ .

(3)、如图3，若E是线段 $A C$ 延长线上的一点， $C E = \frac{1}{2} A C$ ，将菱形 $A B C D$ 绕着点B顺时针旋转 $α °$ $(0 \leq α \leq 360)$ ，请直接写出在旋转过程中 $D E$ 的最大值.

查看试题解析