重庆市彭水苗族土家族自治县2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线 $y = {(x - 2)}^{2} + 1$ 的对称轴是（）

A、 $y$ 轴 B、 $x = - 2$ C、 $x = 2$ D、 $x = 1$

查看试题解析
3. 用配方法解一元二次方程 $x^{2} - 2 x = 3$ 时，此方程可变形为（）

A、 ${(x - 1)}^{2} = 4$ B、 ${(x + 1)}^{2} = 4$ C、 ${(x - 1)}^{2} = 2$ D、 ${(x + 1)}^{2} = 2$

查看试题解析
4. 下列说法错误的是（）

A、不可能事件发生的概率为0 B、随机事件发生的概率为0.5 C、必然事件发生的概率为1 D、随机事件发生的概率介于0和1之间

查看试题解析
5. 若关于 $x$ 的方程 $a x^{2} - x + 2 = 0$ 有两个不相等的实数根，则实数 $a$ 的取值范围为（）

A、 $a < \frac{1}{8}$ B、 $a > \frac{1}{8}$ C、 $a < \frac{1}{8}$ 且 $a \neq 0$ D、 $a = \frac{1}{8}$

查看试题解析
6. 如图，⊙O 是 $△ A B C$ 的外接圆，若 $∠ A = 50 °$ ，则角 $∠ C B O$ 的大小为（）

A、40° B、45° C、50° D、60°

查看试题解析
7. 若将抛物线 $y = 2 x^{2} + 3$ 向右平移3个单位，再向上平移2个单位，则所得抛物线的解析式为（）

A、 $2 k + 9 k - 8 k = 15 ，$ B、 $y = 2 {(x - 3)}^{2} + 5$ C、 $y = 2 {(x + 3)}^{2} - 1$ D、 $y = 2 {(x - 3)}^{2} - 1$

查看试题解析
8. 用一个圆心角为 $60 °$ ，半径为4的扇形作一个圆锥的侧面，则这个圆锥的底面圆半径为（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
9. 在同一坐标系中一次函数 $y = a x + b$ 和二次函数 $y = a x^{2} + b x$ 的图象可能为（）

A、 B、 C、 D、

查看试题解析
10. 在一个袋子中有红，黄，蓝，绿四种颜色的球各一个，从中随机摸出一个小球记录后放回，再随机摸出一个小球，则两次摸出的小球的颜色相同的概率是（）

A、 $\frac{5}{16}$ B、 $\frac{3}{16}$ C、 $\frac{1}{16}$ D、 $\frac{1}{4}$

查看试题解析
11. 如图，AB是⊙O的直径，CD是⊙O的切线，切点为D， CD与AB的延长线交于点C，∠A=30°， $A D = 5$ ，则 $C D$ 的长度为（）

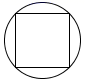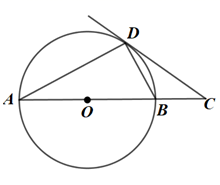A、4 B、5 C、6 D、7

查看试题解析
12. 如图，下列图案均是长度相同的小木棍按一定的规律拼搭而成：第 $1$ 个图案需 $7$ 根小木棍，第 $2$ 个图案需 $13$ 根小木棍，第 $3$ 个图案需 $21$ 根小木棍……，依此规律，第 $8$ 个图案需（　　）根小木棍.

A、85 B、87 C、89 D、91

查看试题解析

二、填空题

13. 点 $A (3 ， - 6)$ 关于原点对称的点的坐标是.

查看试题解析
14. 二次函数 $y = x^{2} + 2 x + m - 1$ 的顶点在 $x$ 轴上，则 $m$ 的值为.

查看试题解析
15. 已知正六边形的边心距为 $\sqrt{3}$ ，则这个正六边形的外接圆的面积为.

查看试题解析
16. 由于技术革新，某种产品的生产成本在逐渐降低，原来每件产品的成本是125元，经过两次降低成本，现在每件的成本是80元，则平均每次降低成本的百分数是.

查看试题解析
17. 从-1，0，1，2这四个数中任取二个不同的数分别作为点P的横、纵坐标，则点P落在抛物线y＝－x²＋x＋2上的概率为.

查看试题解析
18. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，对称轴是 $x = - 1$ ，下列结论：① $a b c > 0$ ，② $2 a - b = 0$ ③ $4 a - 2 b + c < 0$ ，④ ${(a + c)}^{2} - b^{2} < 0$ .其中正确的有.

查看试题解析

三、解答题

19. 计算： ${(- 2)}^{2} + | - 3 | + 2019^{0} - \sqrt{25} + {(\frac{1}{4})}^{- 1}$

查看试题解析
20. 解下列方程：

(1)、 $x^{2} - 2 x = 8 x - 9$ ；

(2)、 $4 x^{2} + 4 x + 9 = 0$ .

查看试题解析
21. 先化简，再求值： $(\frac{4 x - 1}{x^{2} - 1} - \frac{3}{x + 1}) \div \frac{x + 2}{x^{2} - 2 x + 1}$ ，其中 $x$ 为方程 $x^{2} - 2 x - 3 = 0$ 的根.

查看试题解析
22. $△$ ABC在平面直角坐标系xOy中的位置如图所示，A、B、C的坐标分别是(-2，3)、(-1，1)、(0，2).

(1)、作 $△$ ABC关于原点对称的 $△$ A₁B₁C₁ ，并写出点A₁的坐标.

(2)、求 $△$ A₁B₁C₁的面积.

查看试题解析
23. 目前，彭水正处在“脱贫攻坚”的关键阶段，为了调查“脱贫攻坚”工作对广大市民的影响以及公众对“脱贫攻坚”工作的了解程度，彭水县某媒体在全县范围内对“脱贫攻坚”工作开展情况进行调研.问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，分别记作 $A$ ， $B$ ， $C$ ， $D$ ；并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成)，请结合图中所给信息解答下列问题：

(1)、本次被调查的人数共有人；在被调查者中“基本了解”的有人.

(2)、将条形统计图和扇形统计图补充完整.

(3)、在“非常了解”的调查结果里，教师共有5人，其中3男2女，在这5人中，打算随机选出2位进行采访，请你用列表法或树状图的方法求出所选两位教师恰好都是男教师的概率.

查看试题解析
24. 如图，CD是⊙O的直径，弦AB⊥CD于E， $E$ 是 $O D$ 的中点，连接BC， $A O$ ， BD.求 $∠ C$ 的大小.

查看试题解析
25. 某商场经营一种新型台灯，进价为每盏300元.市场调研表明：当销售单价定为400元时，平均每月能销售300盏；而当销售单价每下降1元时，平均每月的销售量就增加10盏.

(1)、当销售单价为多少时，该型台灯的销售利润平均每月能达到40000元？

(2)、临近春节，为了回馈广大顾客，商场部门经理决定在一月份开展降价促销活动，估计分析：若每盏台灯的销售单价在（1）的最高销售单价基础上降价 $m$ %，则可多售出2 $m$ %.要想使一月份的销售额达到209950元，并且保证不亏损，求 $m$ 的值.

查看试题解析
26. 如图，二次函数 $y = \frac{1}{2} x^{2} + b x + c$ 的图象与 $x$ 轴交于B、C两点（点B在点C的左侧），一次函数 $y = k x + 1$ 的图象经过点B和二次函数图象上另一点A. 其中点A的坐标为（4 ，3）.

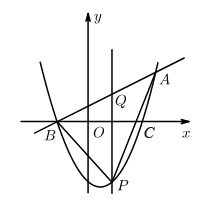(1)、求二次函数和一次函数的解析式；

(2)、若抛物线上的点P在第四象限内，过点P作 $x$ 轴的垂线PQ，交直线AB于点Q，求线段PQ的最大值.

查看试题解析