重庆市开州区2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中是一元二次方程的是（）

A、 $\frac{1}{x} + x^{2} = 0$ B、 $2 x^{2} - 3 = 0$ C、 $4 y - 2 = 0$ D、 $y^{2} - 3 x + 2 = 0$

查看试题解析
2. 下列四个图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 平面直角坐标系中点 $P (- 2 ， 6)$ 关于原点对称的点的坐标是（）

A、 $(2 ， 6)$ B、 $(2 ， - 6)$ C、 $(- 2 ， 6)$ D、 $(- 2 ， - 6)$

查看试题解析
4. 如图， $A B$ 是 $⊙ O$ 的直径，点 $D$ 在 $⊙ O$ 上，若 $∠ A O C = 130 °$ ，则 $∠ B D C$ 的度数是（）

A、70° B、50° C、25° D、40°

查看试题解析
5. 按如图所示的运算程序，若输出的 $y = 9$ ，则输入的 $x$ 值为（）

A、3 B、-3 C、5 D、-5

查看试题解析
6. 将二次函数 $y = 2 x^{2}$ 的图象向右平移1个单位，则平移后的二次函数解析式为（）

A、 $y = 2 x^{2} + 1$ B、 $y = 2 x^{2} - 1$ C、 $y = 2 {(x + 1)}^{2}$ D、 $y = 2 {(x - 1)}^{2}$

查看试题解析
7. 中国的《九章算术》是世界现代数学的两大源泉之一，其中有一问题：“今有牛五、羊二，直金十两，牛二、羊五，直金八两.问牛、羊各直金几何？”译文：今有牛5头，羊2头，共值金10两；牛2头，羊5头，共值金8两.问牛、羊每头各值金多少？设牛、羊每头各值金 $x$ 两、 $y$ 两，依题意，可列出方程组为（）

A、 ${\begin{matrix} 5 x + 2 y = 10 \\ 2 y + 5 x = 8 \end{matrix}$ B、 ${\begin{matrix} 5 x + 2 y = 10 \\ 2 x + 5 y = 8 \end{matrix}$ C、 ${\begin{matrix} 2 x + 5 y = 10 \\ 2 y + 5 x = 8 \end{matrix}$ D、 ${\begin{matrix} 2 x + 5 y = 10 \\ 2 x + 5 y = 8 \end{matrix}$

查看试题解析
8. 下列说法不正确的是（）

A、打开电视剧，电视里播放《小猪佩奇》是偶然事件 B、了解一批灯泡的使用寿命，适合抽样调查 C、一元二次方程 $x^{2} - 2 x + 1 = 0$ 只有一个根 D、甲、乙两人在相同条件下各射击10次，他们的成绩平均数相同，方差分别是 $S_{甲}^{2} = 0.36$ ， $S_{乙}^{2} = 0.54$ ，甲的射击成绩稳定

查看试题解析
9. 已知一元二次方程 $3 x^{2} - 7 x + 4 = 0$ ，则该方程的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、两个根都是自然数根 D、无实数根

查看试题解析
10. 将若干个小菱形按如下图的规律排列：第1个图形有4个小菱形，第2个图形有7个小菱形，第3个图形有10个小菱形， $\dots$ ，则第8个图形有（）个小菱形.

A、24 B、25 C、26 D、27

查看试题解析
11. 若关于 $x$ 的分式方程 $\frac{2 - 6 x}{x - 3} - \frac{2 a}{3 - x} = - 4$ 解为正数，且关于 $y$ 的不等式组 ${\begin{matrix} \frac{y}{2} - 2 \leq \frac{1}{3} (y - 3) \\ 3 y - a \geq 3 (1 - y) \end{matrix}$ 恰有五个整数解，则所有满足条件的整数 $a$ 的和为（）

A、22 B、30 C、32 D、40

查看试题解析
12. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与 $x$ 轴交于 $(1 ， 0)$ 和 $(x_{1} ， 0)$ ，且 $- 2 < x_{1} < - 1$ ，与 $y$ 轴的交点在 $(0 ， 2)$ 上方，有以下结论：① $a b c > 0$ ； ② $2 a - b = 0$ ；③ $3 a + c < 0$ ；④ $0 < \frac{b}{a} < 1$ ；⑤ $a - b < m (a m + b) (m > 1)$ ；其中正确的结论个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 抛物线 $y = - 2 {(x - 1)}^{2} + 1$ 的顶点坐标为.

查看试题解析
14. 某校选修课深受学生喜爱，小雨和小田从“川剧”、“健美操”、“游泳”三门课中任选一门学习，两人恰好都选到“川剧”的概率是.

查看试题解析
15. 如果一元二次方程 $x (x - 6) = 3 (x - 6)$ 的两个根是等腰三角形的两条边的长，那么这个等腰三角形的周长为.

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $A B = 6 ， A D = 4$ ，以点 $A$ 为圆心， $A D$ 长为半径画弧，交 $A B$ 于点 $E$ ，图中阴影部分的面积是（结果保留 $π$ ）.

查看试题解析
17. 小重和小庆相约从学校出发沿同一路线到“开心之洲”玩耍.小重出发1分钟后小庆才出发，小重出发6分钟后发现自己钱包没有带，于是立即掉头并将速度提高为原来的两倍跑步回学校，回学校取到钱包后保持跑步的速度立即赶往“开心之洲”，最终比小庆早1分钟到达.小重两次掉头的时间和取钱包的时间忽略不计，小庆全程保持匀速，小重、小庆相距的路程 $y$ （米）和小庆出发的时间 $t$ （分）之间的函数关系如图所示，则学校到“开心之洲”的路程为米.

查看试题解析
18. 如图，在矩形 $A B C D$ 中， $A B = 4 ， B C = 7$ ， $E A$ 平分 $∠ B A D$ 交 $B C$ 于点 $E$ ，连接 $D E$ ，将矩形 $A B C D$ 沿 $D E$ 翻折，翻折后点 $D$ 与点 $D^{'}$ 点对应，再将所得 $Δ C^{'} D^{'} E$ 绕着点 $E$ 旋转，线段 $C^{'} D^{'}$ 与线段 $E D$ 交于点 $P$ .当 $P D = P C^{'}$ 时，则 $D C^{'}$ 的长为.

查看试题解析

三、解答题

19. 解方程与化简：

(1)、解方程： $3 x^{2} - 2 x - 8 = 0$

(2)、化简： $\frac{x^{2} + 2 x}{x - 1} + (x + 1 - \frac{3}{x - 1})$

查看试题解析
20. 为弘扬开州传统文化，某校开展“言子儿进课堂”的活动，该校随机抽取部分学生，按四个类别： $A$ 表示“很喜欢”， $B$ 表示“喜欢”， $C$ 表示“一般”， $D$ 表示“不喜欢”，调查他们对言子儿的喜欢情况，将结果绘制成如下两幅不完整的统计图，根据图中提供的信息，解决下列问题：

(1)、这次共抽取名学生进行统计调查，扇形统计图中， $D$ 类所对应的扇形圆心角的度数为；

(2)、将条形统计图补充完整；

(3)、若调查的 $A$ 类学生中有2名男生，其余为女生，现从中抽2人进行采访，请画树状图或列表法求刚好选中2名恰好是1男1女的概率.

查看试题解析
21. 如图， $A B$ 是 $⊙ O$ 的直径， $C$ 是 $A B$ 延长线上一点， $C D$ 与 $⊙ O$ 相切于点 $E$ ， $A D ⊥ C D$ 于点 $D$ .

(1)、求证： $A E$ 平分 $∠ D A C$ ；

(2)、若 $A B = 4$ ， $∠ A B E = 60 °$ ，求 $A D$ 的长.

查看试题解析
22. 任何一个数字不全相同的整数，经有限的“重排求差”操作，总会得某一个或一些数，这些数即为黑洞数.“重排求差”即把组成该数的数字重排后得到的最大的数减去重排后得到的最小的数（若差的位数比原位数少，用0补齐）.如四位数7353，组成该数的数字重排后得到的最大数是7533，重排后得到最小数是3357，相减7533-3357=4176，把4176重复一遍；7641-1467=6174，后面发现四位数的黑洞数是6174.

(1)、求证：四位数8392“重排求差”后的数也为黑洞数6174；

(2)、请求出三位数的黑洞数.

查看试题解析

23. 函数的图象在探索函数的性质中有着非常重要的作用，小林同学根据学习函数的经验，探究了函数

y = a x^{2} + b + \frac{1}{2} x | x - 2 |

的图象和性质.

(1)、下表给出了部分

x 、 y

的取值：

$x$	…	-2	-1	0	1	2	3	4	5	…
$y$	…	-2	2	4	4	2	1	0	-1	…

由上表可知， $a =$ ， $b =$ .

(2)、用你喜欢的方法在如图所示的平面直角坐标系中画出函数

y = a x^{2} + b + \frac{1}{2} x | x - 2 |

的图象，并写出函数的一条性质： _▲_.

(3)、若方程

a x^{2} + b + \frac{1}{2} x | x - 2 | = - x + m

恰有两个不同的实数解，请直接写出

m

的取值范围是：.

查看试题解析

24. 开州区扶贫办在精准扶贫中实施产业扶贫，新世纪百货商都积极响应号召，帮助贫困农户进行“举子香肠”和“南门红糖”的销售.“举子香肠”售价是“南门红糖”的两倍，第一个月“举子香肠”和“南门红糖”都卖了 $500 k g$ ，这两种开州特产销售总额为45000元.

(1)、第一个月“举子香肠”和“南门红肠”的售价各是多少元每千克？

(2)、第二个月继续销售这两种特产，第二个月“举子香肠”售价降低了 $3 m %$ ，销量比第一个月增加了 $2 m %$ ，“南门红糖”售价保持不变，销量比第一个月增加了 $\frac{1}{2} m %$ .结果这两种特产第二个月的总销售额比第一个月降低了 $m %$ ，求 $m$ 的值.

查看试题解析
25. 如图，在平面直角坐标系中，一抛物线的对称轴为直线 $x = - 1$ ，与 $y$ 轴负半轴交于点 $C$ ，与 $x$ 轴交于 $A ， B$ 两点，其中点 $A$ 的坐标为 $(- 3 ， 0)$ ，且 $O A = O C$ ， $D$ 为抛物线的顶点.

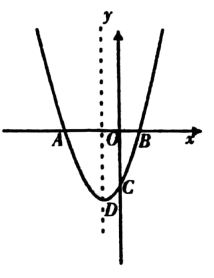(1)、求抛物线的解析式；

(2)、若 $M (- 2 ， y)$ 是抛物线上一点， $P$ 是抛物线上另一点（点 $P$ 与点 $D$ 不重合），当 $S_{Δ B D M} = S_{Δ B P M}$ 时，求出此时点 $P$ 的坐标；

(3)、在（2）的条件下，抛物线对称轴上是否存在点 $Q$ ，使 $Δ B M Q$ 为直角三角形，若存在，请直接写出点 $Q$ 坐标；若不存在，请说明理由.

查看试题解析
26. 如图，在正方形 $A B C D$ 中， $E$ 为边 $B C$ 上一点，过点 $C$ 作 $C F ⊥ A E$ 交 $A E$ 的延长线于点 $F$ ，连接 $D F ， B F$ ，过点 $D$ 作线段 $A F$ 的垂线交 $A F$ 于点 $H$ ，交 $A B$ 于点 $G$ .

(1)、如图1，若 $C F = 1 ， B F = \sqrt{2}$ ，求 $A C$ ；

(2)、如图1，求证： $H G + E F = A H$ ；

(3)、如图2，若正方形的边长为2，点 $E$ 在 $B C$ 边所在直线上运动时，过点 $C$ 作 $C M ⊥ D F$ 交 $D F$ 于点 $M$ ，取 $A D$ 的中点 $N$ ，请直接写出线段 $M N$ 的取值范围.

查看试题解析