浙江省温州市2020-2021学年九年级上学期数学期末考试试卷(二)
试卷更新日期:2021-12-22 类型:期末考试
一、单选题
-
1. 抛物线 与 轴的交点坐标是( )A、 B、 C、 D、2. 如图,四边形 为 的内接四边形,若 ,则 等于( )
 A、 B、 C、 D、3. 一个游戏转盘如图所示,甲、乙、丙、丁四个扇形的圆心角度数分别为 , , , .转动转盘,当其停止转动后,指针落在哪个区域的可能性最大( )
A、 B、 C、 D、3. 一个游戏转盘如图所示,甲、乙、丙、丁四个扇形的圆心角度数分别为 , , , .转动转盘,当其停止转动后,指针落在哪个区域的可能性最大( ) A、甲扇形 B、乙扇形 C、丙扇形 D、丁扇形4. 已知线段 , , 是线段 , 的比例中项,则线段 的长为( )A、4或-4 B、4 C、2 D、85. 将抛物线 平移得到抛物线 ,则这个平移过程正确的是( )A、向上平移2个单位 B、向下平移2个单位 C、向左平移2个单位 D、向右平移2个单位6. 已知一个扇形的半径长是 ,圆心角为 ,则这个扇形的面积为( )A、 B、 C、 D、7. 小明与小亮都是九(1)班的学生,在一次数学综合实践活动中,老师把全班同学随机分成四个小组,那么小明与小亮不在同一个小组的概率为( )A、 B、 C、 D、8. 如图,下列条件不能判定 与 相似的是( )
A、甲扇形 B、乙扇形 C、丙扇形 D、丁扇形4. 已知线段 , , 是线段 , 的比例中项,则线段 的长为( )A、4或-4 B、4 C、2 D、85. 将抛物线 平移得到抛物线 ,则这个平移过程正确的是( )A、向上平移2个单位 B、向下平移2个单位 C、向左平移2个单位 D、向右平移2个单位6. 已知一个扇形的半径长是 ,圆心角为 ,则这个扇形的面积为( )A、 B、 C、 D、7. 小明与小亮都是九(1)班的学生,在一次数学综合实践活动中,老师把全班同学随机分成四个小组,那么小明与小亮不在同一个小组的概率为( )A、 B、 C、 D、8. 如图,下列条件不能判定 与 相似的是( ) A、 B、 C、 D、9. 如图,在 中,点 , 分别在 , 上,且 ,连结 ,若 , ,则 与 的面积比为( )
A、 B、 C、 D、9. 如图,在 中,点 , 分别在 , 上,且 ,连结 ,若 , ,则 与 的面积比为( ) A、 B、 C、 D、10. 如图,在四边形 中,以 为直径的 恰好经过点 , , 交于点 ,已知 平分 , , ,则 的值为( )
A、 B、 C、 D、10. 如图,在四边形 中,以 为直径的 恰好经过点 , , 交于点 ,已知 平分 , , ,则 的值为( )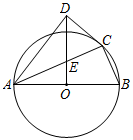 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在 的内接正六边形 中, °.
 12. 某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后,紧接着绿灯开启42秒,再紧接着黄灯开启3秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是.
12. 某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后,紧接着绿灯开启42秒,再紧接着黄灯开启3秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是. 13. 如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为.
13. 如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为. 14. 如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为m.
14. 如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为m.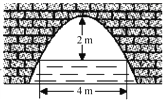 15. 如图,在 中, , , 为 的中点,点 为 上一点,若四边形 为正方形(其中点 , 分别在 , 上),则 的面积为 .
15. 如图,在 中, , , 为 的中点,点 为 上一点,若四边形 为正方形(其中点 , 分别在 , 上),则 的面积为 .
三、解答题
-
16. 某艺术馆一扇窗户(矩形 )上的窗花设计如图所示,已知 , 是矩形 的对角线, , , , 将矩形 分割成 块全等的小矩形, 与 相交于点 , 是 上一点, , 与 相交于点 ,这 块小矩形图案均可以由其中的一块经过一次或两次变换得到.设矩形 的面积为 ,则阴影部分的面积之和为.(用含 的代数式表示).
 17.(1)、已知 ,求 的值;(2)、已知二次函数的图象的顶点坐标为 ,且经过点 ,求该二次函数的解析式.18. 如图,在 中, ,以底边 为直径的 交两腰于点 , .
17.(1)、已知 ,求 的值;(2)、已知二次函数的图象的顶点坐标为 ,且经过点 ,求该二次函数的解析式.18. 如图,在 中, ,以底边 为直径的 交两腰于点 , . (1)、求证: ;(2)、当 是等边三角形,且 时,求 的长.19. 在一个不透明的布袋中放有三个分别标有数 , , 的乒乓球,它们的质地都相同.现从中任意摸出一个球记下所标的数字,将其放回袋中搅匀,再从袋子里任意摸出一个球记下所标的数字.(1)、请用画树状图法或列表法表示出所有可能的结果.(2)、求两次记下的数字的乘积为正数的概率.20. 如图,方格纸中的每个小正方形的边长都是1, 是格点三角形(顶点在方格顶点处).
(1)、求证: ;(2)、当 是等边三角形,且 时,求 的长.19. 在一个不透明的布袋中放有三个分别标有数 , , 的乒乓球,它们的质地都相同.现从中任意摸出一个球记下所标的数字,将其放回袋中搅匀,再从袋子里任意摸出一个球记下所标的数字.(1)、请用画树状图法或列表法表示出所有可能的结果.(2)、求两次记下的数字的乘积为正数的概率.20. 如图,方格纸中的每个小正方形的边长都是1, 是格点三角形(顶点在方格顶点处).
( 1 )在图1中画出一个格点 ,使得 与 相似,周长之比为 ;
( 2 )在图2中画出一个格点 ,使得 与 相似,面积之比为 .
21. 如图,已知抛物线 ,点 是第一象限内抛物线上一个动点,作 轴于点 ,点 是第一象限内抛物线上的另一个点(点 在 的右侧),且 ,作 轴于点 . (1)、当点 是抛物线的顶点时,求点 的坐标;(2)、当点 关于 的对称点 恰好落在 轴上时,求 的长.22. 某礼品公司开有甲、乙两个销售店, 礼品的成本价为每件80元,由于地域的原因,该礼品在甲店的定价是每件120元,每天可以售出20件,在乙店的定价是每件100元,每天可以售出52件,公司为了适当平衡售价,经过市场调查发现,甲店每件 礼品降价1元,可以多售出2件,乙店每件 礼品提价1元,就会少售出2件,设甲店降价与乙店提价的金额相同,均为 元.(1)、当甲、乙两店调价后的售价相同时,每天的利润各是多少元?(2)、设甲店每天的利润为 ,乙店每天的利润为 ,分别求出 , 关于 的函数关系式;(3)、求出这两个销售店每天的的利润之和的最大值以及此时甲店的售价.
(1)、当点 是抛物线的顶点时,求点 的坐标;(2)、当点 关于 的对称点 恰好落在 轴上时,求 的长.22. 某礼品公司开有甲、乙两个销售店, 礼品的成本价为每件80元,由于地域的原因,该礼品在甲店的定价是每件120元,每天可以售出20件,在乙店的定价是每件100元,每天可以售出52件,公司为了适当平衡售价,经过市场调查发现,甲店每件 礼品降价1元,可以多售出2件,乙店每件 礼品提价1元,就会少售出2件,设甲店降价与乙店提价的金额相同,均为 元.(1)、当甲、乙两店调价后的售价相同时,每天的利润各是多少元?(2)、设甲店每天的利润为 ,乙店每天的利润为 ,分别求出 , 关于 的函数关系式;(3)、求出这两个销售店每天的的利润之和的最大值以及此时甲店的售价.

