浙江省衢州市龙游县2020-2021学年九年级上学期数学期末考试试卷

试卷更新日期：2021-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 两个相似三角形周长的比是2:3，则它们的面积比是（）

A、2:3 B、3:2 C、4:9 D、9:4

查看试题解析
2. 下列属于必然事件的是（　　）

A、水中捞月 B、瓮中捉鳖 C、守株待兔 D、大海捞针

查看试题解析
3. 在Rt $△$ ABC中，∠C＝90°，sinA $= \frac{1}{3}$ ，BC＝2，则AB等于（）

A、 $\frac{2}{3}$ B、4 C、4 $\sqrt{2}$ D、6

查看试题解析
4. 如图，直线l₁ $/ /$ l₂ $/ /$ l₃ ，直线AC分别交l₁ ， l₂ ， l₃于点A，B，C；直线DF分别交l₁ ， l₂ ， l₃于点D，E，F.且AB＝3，AC＝8，则 $\frac{D E}{E F}$ 的值为（　　）

A、 $\frac{5}{3}$ B、 $\frac{5}{8}$ C、 $\frac{3}{5}$ D、 $\frac{3}{8}$

查看试题解析
5. 对于抛物线y＝（x﹣1）²﹣3，下列说法错误的是（）

A、抛物线开口向上 B、当x＞1时，y＞0 C、抛物线与x轴有两个交点 D、当x＝1时，y有最小值﹣3

查看试题解析
6. 如图，四边形ADBC内接于⊙O，∠AOB＝122°，则∠ACB等于（　　）

A、131° B、119° C、122° D、58°

查看试题解析
7. 已知二次函数的图象与x轴有两个交点，且顶点坐标为（﹣2，1）．若函数图象经过（1，y₁），（﹣1，y₂），（﹣4，y₃）三点，则（）

A、y₁＜y₃＜y₂ B、y₂＜y₁＜y₃ C、y₁＜y₂＜y₃ D、y₂＜y₃＜y₁

查看试题解析
8. 将二次函数y＝2（x﹣1）²+4图象向左平移3个单位，向下平移2个单位，则平移之后的函数表达式为（　　）

A、y＝2（x+2）²+2 B、y＝2（x+2）²+6 C、y＝2（x﹣4）²+6 D、y＝2（x﹣4）²+2

查看试题解析
9. 如图，在 $△$ ABC中，点D在AB边上，若AD：AB＝2：3，BC＝3，∠ADC＝∠ACB，则线段CD的长为（　　）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、 $\sqrt{6}$ D、2 $\sqrt{3}$

查看试题解析
10. 如图，四边形ABCD是正方形，过点A，B的圆O与射线AD交于点E，过点C的直径与射线AD交于点F，若 $\frac{D F}{D E} = \frac{2}{3}$ ，则tan∠CFD等于（　　）

A、 $\frac{1}{2}$ 或 $\frac{3}{2}$ B、 $\frac{1}{2}$ 或 $\frac{5}{2}$ C、 $\frac{3}{2}$ 或 $\frac{5}{2}$ D、2或 $\frac{5}{2}$

查看试题解析

二、填空题

11. 二次函数y=﹣（x﹣1）²+3图象的顶点坐标是.

查看试题解析
12. 若一个多边形的内角和是900º，则这个多边形是边形.

查看试题解析
13. 两位同学玩“石头、剪子、布”游戏，随机出手一次，两人手势相同的概率是.

查看试题解析
14. 为倡导“低碳生活”，人们常常选择共享单车作为代步工具.图1为单车实物图，图2为单车示意图，AB与地面平行，坐垫C可以在射线BE方向自由调节.已知车轮半径为30cm，BE＝40cm，∠ABE＝75°.小明将坐垫从位置E上移至C，CE＝20cm，则此时坐垫C离地面的高度为cm.（结果精确到1cm）.（参考数据：sin75°＝0.96，cos75°＝0.259，tan75°＝3.732）

查看试题解析
15. 如图，AB是⊙O的直径，四边形ACFE是平行四边形，点E，F在圆上，点C是OB上一点，且OC＝CF，则∠FOC的度数是.

查看试题解析
16. 如图，在Rt $△$ ABC中，∠ACB＝90°，AB＝10，AC＝6，点O是三角形的重心，点D是边AC上一动点，连结并延长DO交AB于点E，将 $△$ ADE沿DE进行翻折得到 $△ A^{'} D E$ ， $A^{'} D$ 与BC交于点F，连结 $A A^{'}$ .

(1)、当点D与点C重合时，则 $A A^{'}$ 的长为.

(2)、BF的最小值为.

查看试题解析

三、解答题

17. 计算：sin30°+cos60°﹣tan45°•tan60°.

查看试题解析
18. 已知二次函数y＝2x²﹣x+1，当﹣1≤x≤1时，求函数y的最小值和最大值.彤彤的解答如下：
解：当x＝﹣1时，则y＝2×（﹣1）²﹣（﹣1）+1＝4；

当x＝1时，则y＝2×1²﹣1+1＝2；

所以函数y的最小值为2，最大值为4.

彤彤的解答正确吗？如果不正确，写出正确的解答.

查看试题解析
19. 如图，在5×5的方格纸中，点A，B均在格点上，请按要求画图.①仅用无刻度直尺，且不能用直尺中的直角：②保留作图痕迹.

(1)、在图1中过点B画线段AB的垂线l；

(2)、在图2画一个面积为2的格点 $△$ ABC.

查看试题解析
20. 如图，AB是⊙O的直径，点C是⊙O上一点，连接BC，AC，点E是BC的中点，连结并延长OE交圆于点D．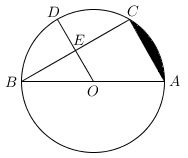

(1)、求证：OD $/ /$ AC．

(2)、若DE＝2，BE＝2 $\sqrt{3}$ ，求阴影部分的面积．

查看试题解析
21. 一个黑箱子里装有红、白两种颜色的球4只，他们除颜色外，其他都相同，小明将球搅匀后从箱子中随机摸出一个球，记下颜色，再把它放回不断重复实验，将多次实验结果画出如下频率统计图.

(1)、当摸球次数很大时，摸到白球的频率将会接近（精确到0.01），从箱子中摸一次球，摸到红球的概率是；

(2)、从该箱子里随机摸出一个球，不放回，再摸出一个球.用树状图或列表法求出摸到一个红球一个白球的概率.

查看试题解析
22. 已知二次函数y＝ax²﹣bx+3（a≠0）的图象过点A(2，3)，交y轴于点B.

(1)、求点B的坐标及二次函数图象的对称轴；

(2)、若抛物线最高点的纵坐标为4，求二次函数的表达式；

(3)、已知点(m，y₁)，(n，y₂)在函数图象上且0＜m＜n＜1，试比较y₁和y₂的大小.

查看试题解析
23. 若四边形的一组对角α，β，满足∠α $+ \frac{1}{2}$ ∠β＝180°，我们把这个四边形称为可衍生四边形，∠β为二倍角.

(1)、如图1，在四边形ABCD中，AD⊥CD，∠A＝130°，当四边形ABCD为可衍生四边形，且∠C为二倍角时，求∠B的度数；

(2)、如图2，四边形ABCD内接于⊙O，点E是圆上一点，连结并延长CE，AD交于点F，延长CD，BA交于点G，CD•DG＝AD•DF，求证：四边形ABCF是可衍生四边形；

(3)、如图3，在（2）的条件下，连结AE，EG，若CD是⊙O的直径，AF⊥EG，AG＝5AB，求sin∠FAG的值.

查看试题解析
24. 如图，在等边 $△$ ABC的AC，BC边上各取一点E，D，使AE＝CD，AD，BE相交于点O.

(1)、求证：AD＝BE；

(2)、若BO＝6OE $= \frac{12 \sqrt{7}}{7}$ ，求CD的长.

(3)、在（2）的条件下，动点P在CE上从点C向终点E匀速运动，点Q在BC上，连结OP，PQ，满足∠OPQ＝60°，记PC为x，DQ的长为y，求y关于x的函数表达式.

查看试题解析