黑龙江省哈尔滨十七中2020-2021学年九年级下学期数学开学考试试卷
试卷更新日期:2021-12-22 类型:开学考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、(﹣a2)3=﹣a5 B、a2•a6=a8 C、4a2﹣2a2=2 D、a6÷a2=a33. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、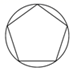 D、
D、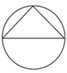 4. 七个大小相同的正方体搭成的几何体如图所示,其左视图是( ).
4. 七个大小相同的正方体搭成的几何体如图所示,其左视图是( ).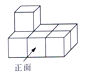 A、
A、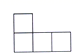 B、
B、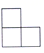 C、
C、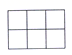 D、
D、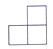 5. 反比例函数y= 的图象经过点(3,﹣2),下列各点在图象上的是( )
5. 反比例函数y= 的图象经过点(3,﹣2),下列各点在图象上的是( )
A、(﹣3,﹣2) B、(3,2) C、(﹣2,﹣3) D、(﹣2,3)6. 不等式组 的整数解的个数是( )A、6 B、5 C、4 D、37. 分式方程 =1的解是( )A、x=1 B、x=﹣1 C、x=3 D、x=﹣38. 如图,线杆DC的高度为 ,两根拉线 与 互相垂直, ,若 、 、 在同一条直线上,则拉线 的长度为( ) A、 B、 C、 D、9. 如图,点E是▱ABCD的边BC延长线上一点,连接AE交CD于点F , 则下列结论中一定正确的是( )
A、 B、 C、 D、9. 如图,点E是▱ABCD的边BC延长线上一点,连接AE交CD于点F , 则下列结论中一定正确的是( )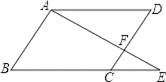 A、 B、 C、 D、10. 甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时向t(分)之间的函数关系如图所示,下列说法中正确的是( )
A、 B、 C、 D、10. 甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时向t(分)之间的函数关系如图所示,下列说法中正确的是( )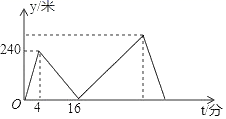 A、甲步行的速度为8米/分 B、乙走完全程用了34分钟 C、乙用16分钟追上甲 D、乙到达终点时,甲离终点还有360米
A、甲步行的速度为8米/分 B、乙走完全程用了34分钟 C、乙用16分钟追上甲 D、乙到达终点时,甲离终点还有360米二、填空题
-
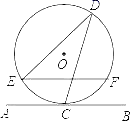
11. 把13000用科学记数法表示为 .12. 函数 中,自变量x的取值范围是 .13. 分解因式:3a3﹣6a2+3a= .14. 计算: .15. 笔简中有10支型号、颜色完全相同的铅笔,将它们逐一标上1﹣10的号码,若从笔筒中任意抽出一支铅笔,则抽到编号是3的倍数的概率是.16. 将抛物线y=(x+1)2﹣2向右平移1单位,得到的抛物线与y轴的交点的坐标是 .17. 一个扇形的面积为4πcm2 , 弧长为2πcm , 则此扇形的圆心角为度.18. 如图,直线AB与半径为4的⊙O相切于点C , 点D在⊙O上,连接CD , DE , 且∠EDC=30°,弦EF∥AB , 则EF的长为 .
 19. 在△ABC中,点O是不与A、B、C重合的点,且满足OA=OB=OC , 若∠BOC=140°,则∠BAC= .20. 如图,在△ABC中,∠ACB=90°,点D在边AB上,CD平分△ABC的周长,点E在BC上,且2∠BDE=∠A , 若AC=15,BE=3,则CE的长为 .
19. 在△ABC中,点O是不与A、B、C重合的点,且满足OA=OB=OC , 若∠BOC=140°,则∠BAC= .20. 如图,在△ABC中,∠ACB=90°,点D在边AB上,CD平分△ABC的周长,点E在BC上,且2∠BDE=∠A , 若AC=15,BE=3,则CE的长为 .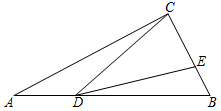
三、解答题
-
21. 先化简再求值 ,其中 .22. 在6×4的方格纸中,△ABC的三个顶点都在格点上
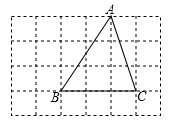
( 1 )在图中画出线段BD , 使BD∥AC , 其中D是格点;
( 2 )在图中画出线段BE , 使BE⊥AC , 其中E是格点,连接DE , 并直接写出∠BED的度数.
23. 为了增强学生的环保意识,某校团委组织了一次“环保知识”考试,考题共10题考试结束后,学校团委随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题: (1)、“答对10题”所对应扇形的心角为;(2)、通过计算补全条形统计图;(3)、若该校共有2000名学生参加这次“环保知识”考试,请你估计该校答对不少于8题的学生人数.24. 已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)、“答对10题”所对应扇形的心角为;(2)、通过计算补全条形统计图;(3)、若该校共有2000名学生参加这次“环保知识”考试,请你估计该校答对不少于8题的学生人数.24. 已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.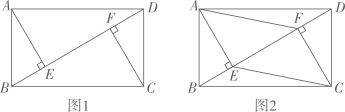 (1)、如图1,求证:AE=CF;(2)、如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的 .25. 在运动会前夕,光明中学都会购买篮球、足球作为奖品.若购买6个篮球和8个足球共花费1700元,且购买一个篮球比购买一个足球多花50元.(1)、求购买一个篮球,一个足球各需多少元;(2)、今年学校计划购买这种篮球和足球共10个,恰逢商场在促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1150元,则最多可购买多少个?26. 如图,△ABC内接于⊙O , 弦AD平分∠BAC , AD交BC于点E , 且BE=CE .
(1)、如图1,求证:AE=CF;(2)、如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的 .25. 在运动会前夕,光明中学都会购买篮球、足球作为奖品.若购买6个篮球和8个足球共花费1700元,且购买一个篮球比购买一个足球多花50元.(1)、求购买一个篮球,一个足球各需多少元;(2)、今年学校计划购买这种篮球和足球共10个,恰逢商场在促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1150元,则最多可购买多少个?26. 如图,△ABC内接于⊙O , 弦AD平分∠BAC , AD交BC于点E , 且BE=CE . (1)、如图1,求证:AD为⊙O的直径;(2)、如图2,点P为弧CD上一点,连接AP交BC于点F , 过点P作⊙O的切线,交BC的延长线于点G , GH⊥PF于点H , 求证:PH=FH;(3)、如图3,在(2)的条件下,连接DF , 且∠DFB=3∠PAD , 点R在CG上,连接DR , DR交GH于点N , RN=RG , HN=1,DF=5,求DE的长.27. 如图1,在平面直角坐标系中,点O为坐标原点,直线y=kx﹣1交x轴正半轴于点A , 交y轴负半轴于点B , AB= .
(1)、如图1,求证:AD为⊙O的直径;(2)、如图2,点P为弧CD上一点,连接AP交BC于点F , 过点P作⊙O的切线,交BC的延长线于点G , GH⊥PF于点H , 求证:PH=FH;(3)、如图3,在(2)的条件下,连接DF , 且∠DFB=3∠PAD , 点R在CG上,连接DR , DR交GH于点N , RN=RG , HN=1,DF=5,求DE的长.27. 如图1,在平面直角坐标系中,点O为坐标原点,直线y=kx﹣1交x轴正半轴于点A , 交y轴负半轴于点B , AB= .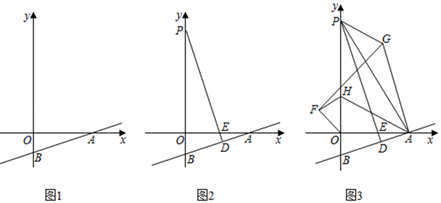 (1)、求k的值;(2)、如图2,P为y轴正半轴上一点,过点P作PD⊥AB于点D , 交线段OA于点E , 设点P的纵坐标为t , 线段AD的长d , 求d与t的函数解析式;(3)、如图3,在(2)的条件下,d= ,点H在线段OP上,连接AH , AH=HP , 点G为第一象限内直线AP上方一点,连接PG、AG , ∠APG=30°,点F为第二象限内一点,连接OF、FH、FG , 若FG=AG , ∠AHO+2∠OHF=180°,∠APG+∠AGF=2∠FOH , ∠AGF﹣∠FOH=15°,求点F的坐标.
(1)、求k的值;(2)、如图2,P为y轴正半轴上一点,过点P作PD⊥AB于点D , 交线段OA于点E , 设点P的纵坐标为t , 线段AD的长d , 求d与t的函数解析式;(3)、如图3,在(2)的条件下,d= ,点H在线段OP上,连接AH , AH=HP , 点G为第一象限内直线AP上方一点,连接PG、AG , ∠APG=30°,点F为第二象限内一点,连接OF、FH、FG , 若FG=AG , ∠AHO+2∠OHF=180°,∠APG+∠AGF=2∠FOH , ∠AGF﹣∠FOH=15°,求点F的坐标.