浙江省台州市温岭市五校2021-2022学年九年级上学期数学期中考试试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 下列图案中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 由二次函数y=3(x﹣4)2﹣2可知( )A、其图象的开口向下 B、其图象的对称轴为直线x=4 C、其顶点坐标为(4,2) D、当x>3时,y随x的增大而增大4. 已知一元二次方程 有一个根为3,则 的值为( )A、2 B、 C、4 D、5. 小敏在某次投篮中,篮球的运动路线是抛物线 3.5的一部分(如图),若命中篮圈中心,则他与篮底的水平距离 是( )
2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 由二次函数y=3(x﹣4)2﹣2可知( )A、其图象的开口向下 B、其图象的对称轴为直线x=4 C、其顶点坐标为(4,2) D、当x>3时,y随x的增大而增大4. 已知一元二次方程 有一个根为3,则 的值为( )A、2 B、 C、4 D、5. 小敏在某次投篮中,篮球的运动路线是抛物线 3.5的一部分(如图),若命中篮圈中心,则他与篮底的水平距离 是( ) A、3.5m B、3.8m C、4m D、4.5m6. 如图, 在 中, , 在同一平面内, 将 绕点 旋转到 的位置, 使得 , 则 是( )
A、3.5m B、3.8m C、4m D、4.5m6. 如图, 在 中, , 在同一平面内, 将 绕点 旋转到 的位置, 使得 , 则 是( ) A、 B、 C、 D、7. 等腰三角形的底边长为6,腰长是方程 的一个根,则该等腰三角形的周长为( )A、12 B、16 C、l2或16 D、158. 如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4 ,OC=10,O′为△ABC外一点,且△CBO≌△ABO′,则四边形AO′BO的面积为( )
A、 B、 C、 D、7. 等腰三角形的底边长为6,腰长是方程 的一个根,则该等腰三角形的周长为( )A、12 B、16 C、l2或16 D、158. 如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4 ,OC=10,O′为△ABC外一点,且△CBO≌△ABO′,则四边形AO′BO的面积为( ) A、10 B、16 C、40 D、809. 拋物线 为常数 开口向下且过点 ,下列结论:(1) ;(2) ;(3) ;(4) ,若方程有两个不相等的实数根, 则 . 其中正确结论的个数是( )A、4 B、3 C、2 D、110. 如图, 在平面直角坐标系中放置 , 点 .现将 沿 轴的正方向无滑动翻转,依次得到 连续翻转 14 次, 则经过 三顶点的抛物线解析式为( )
A、10 B、16 C、40 D、809. 拋物线 为常数 开口向下且过点 ,下列结论:(1) ;(2) ;(3) ;(4) ,若方程有两个不相等的实数根, 则 . 其中正确结论的个数是( )A、4 B、3 C、2 D、110. 如图, 在平面直角坐标系中放置 , 点 .现将 沿 轴的正方向无滑动翻转,依次得到 连续翻转 14 次, 则经过 三顶点的抛物线解析式为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 点 与点 关于原点对称, 则点 坐标是.12. 如果 是一元二次方程 的一个根,那么 的值是.13. 将二次函数 的图象先向右平移3个单位长度,再向上平移5个单位长度,得到的图象的函数解析式是.14. 某小组有若干人, 新年大家互相发一条微信视福, 已知全组共发微信56条,则这个小组的人数为人.15. 我们把横坐标、纵坐标均为整数的点叫做整点, 如 等等. 若抛物线 与x轴围成的封闭区域(含边界)恰好含有8个整点,则实数 的取值范围是.
 16. 如图, 已知 中, , 动点 满足 , 将线段 绕点 顺时针旋转 得到线段 , 连接 , 则 的最大值为.
16. 如图, 已知 中, , 动点 满足 , 将线段 绕点 顺时针旋转 得到线段 , 连接 , 则 的最大值为.
三、解答题
-
17. 解方程:(1)、(2)、18. 若关于 的一元二次方程 有两个不相等的实数根,(1)、求 的取值范围;(2)、 取符合条件的最小整数时, 求此方程的根.19. 如图, 线段 两端点坐标分别为 .
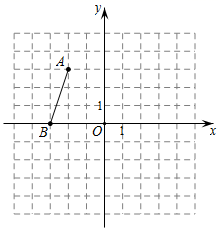 (1)、作出线段 绕点 逆时针旋转 后得到的线段 ;(2)、点 的坐标为 ,若线段 上有一点 , 则在线段 上的对应点 的 坐标为.(3)、若将线段 绕着某点旋转 恰好得到线段 , 点 与点 , 点 与点 是对应点,已知点 . 请通过无刻度的直尺画图找到旋转中心,将其标记为 .(保留作图痕迹)20. 已知一个二次函数图象上部分点的横坐标 与纵坐标 的对应值如下所示:
(1)、作出线段 绕点 逆时针旋转 后得到的线段 ;(2)、点 的坐标为 ,若线段 上有一点 , 则在线段 上的对应点 的 坐标为.(3)、若将线段 绕着某点旋转 恰好得到线段 , 点 与点 , 点 与点 是对应点,已知点 . 请通过无刻度的直尺画图找到旋转中心,将其标记为 .(保留作图痕迹)20. 已知一个二次函数图象上部分点的横坐标 与纵坐标 的对应值如下所示:0
1
0
0
 (1)、求这个二次函数的表达式, 并画出图象;(2)、当 时, 直接写出 的取值范围;(3)、若该图象与 轴的两交点分别记为 , 且 在 的左侧, 点 在该二次函数图象上, 求 的面积.21. 如图, 在等腰三角形 中, 是 边上一点, 把点 绕点 按逆时针方向旋转 到点 ,连接 ,
(1)、求这个二次函数的表达式, 并画出图象;(2)、当 时, 直接写出 的取值范围;(3)、若该图象与 轴的两交点分别记为 , 且 在 的左侧, 点 在该二次函数图象上, 求 的面积.21. 如图, 在等腰三角形 中, 是 边上一点, 把点 绕点 按逆时针方向旋转 到点 ,连接 , (1)、求证: .(2)、当点 在同一条直线上时, 求证: .22. 阅读下面的材料, 回答问题: 解方程 +4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是设 , 那么 , 于是原方程可变为 (1), 解得 ,
(1)、求证: .(2)、当点 在同一条直线上时, 求证: .22. 阅读下面的材料, 回答问题: 解方程 +4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是设 , 那么 , 于是原方程可变为 (1), 解得 ,当 时, ;
当 时, ;
原方程有四个根: .
在由原方程得到方程(1)的过程中, 利用换元法达到降次的目的, 体现了数学的转化思想.
(1)、试用上述方法解方程: ,得原方程的解为 .(2)、解方程 .23. 某数学兴趣小组经过市场调研, 整理出某种商品的销售信息, 该商品进价60元,如果每件卖95元每天可售出46件, 每件销售价格每增加5元, 每天销售会减少2件, 设每件销售价格增加 元, 每天售出 件, 市场管理部门规定, 该种商品每件利润不能超过60元.(1)、 与 之间的函数解析式为.(2)、求出当 为多少时, 每天销售这种商品可获利润2090元.(3)、设每天销吿这种商品可获得利润 元, 当 为多少时, 最大, 最大利润是多少?24. 如图1, 矩形 中, ,将矩形 绕着点 顺时针旋转, 得到矩形 . (1)、当点 落在 上时, 则线段 的长度等于;(2)、如图2,当点 落在 上吋, 则 的面积为 ;(3)、如图3,连接 , 判断 与 的位置关系并说明理由;(4)、在旋转过程中, 求出 的最大值.
(1)、当点 落在 上时, 则线段 的长度等于;(2)、如图2,当点 落在 上吋, 则 的面积为 ;(3)、如图3,连接 , 判断 与 的位置关系并说明理由;(4)、在旋转过程中, 求出 的最大值.