浙江省衢州市教学联盟体2021-2022学年九年级上学期数学期中考试试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 在一个装有黑色围棋的盒子中摸出一颗棋子,摸到一颗白棋是( )A、必然事件 B、不确定事件 C、不可能事件 D、无法判断2. 二次函数y=(x﹣4)2﹣1的顶点坐标是( )A、(﹣4,﹣1) B、(﹣4,1) C、(4,﹣1) D、(4,1)3. 下列标志图中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 半径为5的⊙O,圆心在直角坐标系的原点O,则点P(3,4)与⊙O的位置关系是( ).A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定5. 将二次函数y=x2的图象向右平移2个单位,再向上平移1个单位,所得图象的表达式是( )A、y=(x﹣2)2+1 B、y=(x+2)2+1 C、y=(x﹣2)2﹣1 D、y=(x+2)2﹣16. 已知圆心角为120°的扇形面积为12π,那么扇形的弧长为( )
4. 半径为5的⊙O,圆心在直角坐标系的原点O,则点P(3,4)与⊙O的位置关系是( ).A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定5. 将二次函数y=x2的图象向右平移2个单位,再向上平移1个单位,所得图象的表达式是( )A、y=(x﹣2)2+1 B、y=(x+2)2+1 C、y=(x﹣2)2﹣1 D、y=(x+2)2﹣16. 已知圆心角为120°的扇形面积为12π,那么扇形的弧长为( )
A、4 B、2 C、4π D、2π7. 若点A(﹣4,y1),B(﹣1,y2),C(1,y3)都是二次函数y=x2+4x+k的图象上的点,则( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y2<y1 D、y3<y1<y28. 一块圆形宣传标志牌如图所示,点 , , 在 上, 垂直平分 于点 ,现测得 , ,则圆形标志牌的半径为( )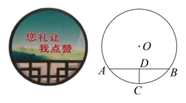 A、 B、 C、 D、9. 如图,半径为5的 中,弦 , 所对的圆心角分别是 , .已知 , ,则弦 的弦心距等于
A、 B、 C、 D、9. 如图,半径为5的 中,弦 , 所对的圆心角分别是 , .已知 , ,则弦 的弦心距等于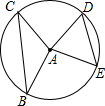 A、 B、 C、4 D、310. 如图,正方形ABCD的边长为3,将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在AB上滑动,同时点F在BC上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段QF的中点M所经过的路线长为( )
A、 B、 C、4 D、310. 如图,正方形ABCD的边长为3,将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在AB上滑动,同时点F在BC上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段QF的中点M所经过的路线长为( )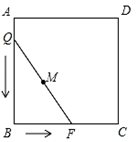 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知二次函数 的图象开口向下,则m的取值范围是 .
12. 如图,在圆内接四边形ABCD中,若∠C=80°,则∠A等于.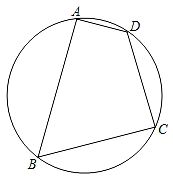 13. 学校组织秋游,安排给九年级3辆车,小明和小慧都可以从这3辆车中任选一辆搭乘.则小明和小慧同车的概率为.14. 如果一个正n边形的每个内角是140°,则n=.15. 如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为.
13. 学校组织秋游,安排给九年级3辆车,小明和小慧都可以从这3辆车中任选一辆搭乘.则小明和小慧同车的概率为.14. 如果一个正n边形的每个内角是140°,则n=.15. 如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为.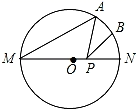 16. 已知二次函数y=﹣(x﹣a)2+a+2,当a取不同的值时,顶点在一条直线上,这条直线的解析式是 . 抛物线与y轴交点为C , 当﹣1≤a≤2时,C点经过的路径长为 .
16. 已知二次函数y=﹣(x﹣a)2+a+2,当a取不同的值时,顶点在一条直线上,这条直线的解析式是 . 抛物线与y轴交点为C , 当﹣1≤a≤2时,C点经过的路径长为 .三、解答题
-
17. 解下列方程(1)、(2)、18. 已知二次函数的图象以点A(﹣1,4)为顶点,且过点B(2,﹣5).(1)、求抛物线解析式;(2)、试判断该二次函数的图象是否经过点(1,2).19. “优学常山”是近年常山教育的新目标,现在有分别标有汉字“优”、“学”、“常”、“山”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.(1)、若从中任取一个球,球上的汉字是“学”的概率是多少.(2)、甲从中任取一球,不放回,再从中任取一球,请用画树状图或列表的方法,求出甲取出的两个球上的汉字恰能组成“常山”的概率P.20. 如图,AB是⊙O的直径,C,D是⊙O上的点,且 ,AD分别与BC,OC相交于点E,F.
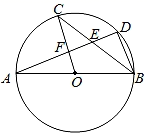 (1)、求证:CB平分∠ABD;(2)、若AB=8,AD=6,求CF的长.21. 如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).
(1)、求证:CB平分∠ABD;(2)、若AB=8,AD=6,求CF的长.21. 如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).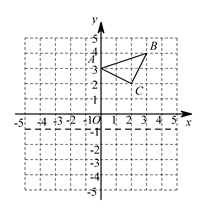
( 1 )画出△ABC关于原点O的中心对称图形△A1B1C1;
( 2 )画出将△ABC绕原点逆时针方向旋转90°后的图△A2B2C2.
( 3 )求△A2B2C2的面积.
22. 为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)、试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)、当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)、为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
23. 《函数的图象与性质》拓展学习片段展示: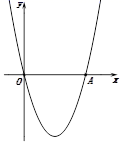
 (1)、(问题)
(1)、(问题)
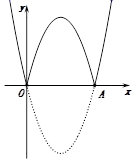
如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a= , 点A的坐标为 .(2)、(操作)
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式:.(3)、(探究)
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是.(4)、(应用)结合上面的操作与探究,继续思考: 如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
求A、B两点的坐标;(用含h的式子表示)(5)、当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.24. 如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过B、C两点,与x轴另一交点为A,顶点为D.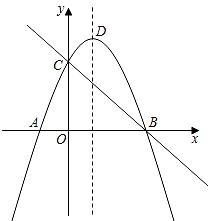 (1)、求抛物线的解析式.(2)、如果一个圆经过点O、点B、点C三点,并交于抛物线AC段于点E,求∠OEB的度数.(3)、在抛物线的对称轴上是否存在点P,使△PCD为等腰三角形,如果存在,求出点P的坐标,如果不存在,请说明理由.
(1)、求抛物线的解析式.(2)、如果一个圆经过点O、点B、点C三点,并交于抛物线AC段于点E,求∠OEB的度数.(3)、在抛物线的对称轴上是否存在点P,使△PCD为等腰三角形,如果存在,求出点P的坐标,如果不存在,请说明理由.