山西省平定县四校校联2021-2022学年八年级上学期数学期中试卷
试卷更新日期：2021-12-22 类型：期中考试
一、单选题
-
1. 中国文字博大精深，而且有许多是轴对称图形，在这四个文字中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 用三角尺可按下面方法画角平分线：在已知的∠AOB的两边上，分别取OM＝ON，再分别过点M，N作OA，OB的垂线，交点为P，画射线OP，则OP平分∠AOB.做法中用到证明△OMP与△ONP全等的判定方法是（ ）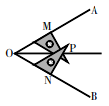
A、SAS B、SSS C、ASA D、HL3. 如图所示，在△ABC中，AB＝AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E，F．则图中全等三角形共有（ ）
A、2对 B、3对 C、4对 D、5对4. 下列命题中，是真命题的是（ ）
①两条直线被第三条直线所截，同位角相等；
②在同一平面内，垂直于同一直线的两条直线互相平行
③三角形的三条高中，必有一条在三角形的内部
④三角形的三个外角一定都是锐角A、①② B、②③ C、①③ D、③④5. 如图，△ABC与△A′B′C′关于直线MN对称，BB′交MN于点O，则下列结论不一定正确的是（ ）
A、AC＝A′C′ B、BO＝B′O C、AA′⊥MN D、AB B′C′6. 如图， ，则图中全等三角形共有（ ）
A、1对 B、2对 C、3对 D、4对7. 如图，把长方形 沿EF对折，若 ，则 的度数为（ ）
A、 B、 C、 D、8. 下列正多边形地砖中，单独选用一种地砖不能铺满地面的是（ ）A、正三角形地砖 B、正方形地砖 C、正六边形地砖 D、正八边形地砖9. 如图，在平面直角坐标系中，点A的坐标为（3，2），△AOB为等腰直角三角形，∠AOB＝90°，则点B的坐标为（ ）
A、（2，3） B、（﹣2，3） C、（﹣3，2 D、（﹣1.5，3）10. 如图，△ABC的两条高BD、CE相交于点O，且OB=OC．则下列结论：①△BEC≌△CDB，②△ABC是等腰三角形，③AE=AD，④点O在∠BAC的平分线上，其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如果一个多边形的内角和为1620°，那么这个多边形的一个顶点有条对角线．12. 已知：如图， ，则 度．
13. 如图，△ABC中，∠A＝80°，剪去∠A后，得到四边形BCDE，则∠1＋∠2＝。
14. 如图，已知方格纸中是4个相同的正方形，则 度.
15. 课间，小聪拿着老师的等腰直角三角板玩，不小心掉到两墙之间（如图）， ， ，从三角板的刻度可知 ，小聪很快就知道了砌墙砖块的厚度的平方（每块砖的厚度相等）为 2 ．
三、解答题
-
16. 已知：如图，MS⊥PS，MN⊥SN，PQ⊥SN，垂足分别为S，N，Q，且MS＝PS．求证：△MNS≌△SQP．
17. 在△ABC中，∠C=90° ， ∠B=15° ， DE是AB的中垂线，BE=5，则求AC的长.
18. 如图，已知等腰 的顶角 ．
(1)、根据要求用尺规作图：作 的平分线交 于点 ；（不写作法，只保留作图痕迹．）(2)、在（1）的条件下，证明： 是等腰三角形．19. 如图， 中， ，点P在AB上， ， ，垂足分别为D，E，已知 ，求BE的长．
20. 如图，已知在Rt△ABC中，AB=AC，∠BAC=90°，AN是过点A的任一直线，BD⊥AN于点D，CE⊥AN于点E．求证：BD﹣CE=DE．
21. 已知：如图，锐角 的两条高 相交于点 ，且
(1)、求证： 是等腰三角形；(2)、判断点 是否在 的角平分线上，并说明由.22. 如图，已知△ABC和△CDE均为等边三角形，且点B、C、D在同一条直线上，连接AD、BE ， 交CE和AC分别于G、H点，连接GH ．
(1)、求证：AD＝BE；(2)、求证：△BCH≌△ACG；(3)、试猜想：△CGH是什么特殊的三角形，并加以说明．23. 通过对下面数学模型的研究学习，解决下列问题：
(1)、如图1，∠BAD＝90°，AB＝AD，过点B作BC⊥AC于点C，过点D作DE⊥AC于点E。由∠1+∠2＝∠2+∠D＝90°，得∠1＝∠D。又∠ACB＝∠AED＝90°，可以推理得到△ABC≌△DAE。进而得到AC＝ ， BC＝AE。我们把这个数学模型称为“K字”模型或“一线三等角”模型；(2)、如图2，∠BAD＝∠CAE＝90°，AB＝AD，AC＝AE，连接BC，DE，且BC⊥AF于点F，DE与直线AF交于点G．求证：点G是DE的中点；(3)、如图，已知四边形ABCD和DEGF为正方形，△AFD的面积为S1 ， △DCE的面积为S2 ， 则有S1S2（填“＞、＝、＜”）