山东省济南市商河县五校联考2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数中的无理数是（　　）

A、 $\sqrt{4}$ B、π C、 $\frac{10}{7}$ D、0.1

查看试题解析
2. $\sqrt{9}$ 的值等于 $($ $)$

A、3 B、-3 C、±3 D、 $\sqrt{3}$

查看试题解析
3. 点A（﹣5，3）所在的象限是（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 满足下列条件的△ABC，不是直角三角形的为（）

A、∠A=∠B－∠C B、∠A∶∠B∶∠C=1∶1∶2 C、b²=a²－c² D、a∶b∶c=2∶3∶4

查看试题解析
5. 下列运算中，正确的是（　　）

A、5 $\sqrt{3}$ ﹣2 $\sqrt{3}$ ＝3 B、2 $\sqrt{2}$ ×3 $\sqrt{2}$ ＝6 C、2 $\sqrt{3}$ +3 $\sqrt{2}$ ＝5 $\sqrt{5}$ D、3 $\sqrt{3}$ ÷ $\sqrt{3}$ ＝3

查看试题解析
6. 如图，根据图中标注在点A所表示的数为（）

A、﹣ $\sqrt{5}$ B、﹣1﹣ $\sqrt{5}$ C、﹣1＋ $\sqrt{5}$ D、1﹣ $\sqrt{5}$

查看试题解析
7. 已知点（﹣4，y₁），（2，y₂）都在直线y=﹣ $\frac{1}{2}$ x+2上，则y₁ ， y₂大小关系是（）

A、y₁＞y₂ B、y₁=y₂ C、y₁＜y₂ D、不能比较

查看试题解析
8. 在平面直角坐标系中，若点M（﹣2，3）与点N（﹣2，y）之间的距离是5，那么y的值是（）

A、﹣2 B、8 C、2或8 D、﹣2或8

查看试题解析
9. 已知正比例函数y＝kx的图象如图所示，则一次函数y＝kx﹣k的图象是（）

A、 B、 C、 D、

查看试题解析
10. 观察下列式子： $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 \frac{1}{2}$ ； $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 \frac{1}{6}$ ； $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 \frac{1}{12}$ ；……，根据此规律，若 $\sqrt{1 + \frac{1}{a^{2}} + \frac{1}{b^{2}}} = 1 \frac{1}{90}$ ，则a²＋b²的值为（）.

A、110 B、164 C、179 D、181

查看试题解析
11. 如图，在2×2的方格中，小正方形的边长是1，则AC边上的高为（）

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{3}{2} \sqrt{2}$ C、 $\sqrt{5}$ D、 $\frac{3}{2}$

查看试题解析
12. A，B两地相距30km，甲乙两人沿同一条路线从A地到B地．如图，反映的是两人行进路程y（km）与行进时间t（h）之间的关系，①甲始终是匀速运动，乙的行进不是匀速的；②乙用了5个小时到达目的地；③乙比甲迟出发0.5小时，④甲在出发5小时后被乙追上．以上说法正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 8的立方根是．

查看试题解析
14. 已知 ${(a + 6)}^{2} + \sqrt{b - 3} = 0$ ，则 ${(a + b)}^{2} =$ ．

查看试题解析
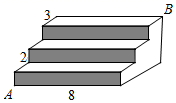
15. 计算：（ $\sqrt{3}$ +2）²⁰¹⁴（ $\sqrt{3}$ ﹣2）²⁰¹⁵＝．

查看试题解析
16. 已知点A（m，3），B（﹣1，n）关于x轴对称，则mn的值为．

查看试题解析
17. 如图，三级台阶，每一级的长、宽、高分别为8dm、3dm、 $2 d m$ ，A和B是这个台阶上两个相对的端点，点A处有一只蚂蚁，想到点B处去吃可口的食物，则蚂蚁沿着台阶面爬行到点B的最短路程为dm．

查看试题解析
18. 如图，在一单位为1的方格纸上， $△ A_{1} A_{2} A_{3} ， △ A_{3} A_{4} A_{5} ， △ A_{5} A_{6} A_{7} \dots \dots$ ，都是斜边在x轴上，斜边长分别为2，4，6，……的等腰直角三角形，若 $A_{1} A_{2} A_{3}$ 的顶点坐标分别为 $A_{1} (2 ， 0) ， A_{2} (1 ， - 1) ， A_{3} (0 ， 0)$ ，则依图中所示规律， $A_{2020}$ 的坐标为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\frac{\sqrt{8} + \sqrt{18}}{\sqrt{2}}$ ；

(2)、 $\sqrt{27}$ ﹣ $\sqrt{12} + \sqrt{\frac{1}{3}}$ ．

查看试题解析
20. 计算题

(1)、 $\sqrt[3]{8} + {(- \frac{1}{2})}^{- 1} + {(- 1)}^{2018}$ ；

(2)、 $(1 + \sqrt{2}) \times (1 - \sqrt{2}) + {(\sqrt{3} + 2)}^{0} + | 2 - \sqrt{3} |$ ．

查看试题解析
21.

(1)、利用平方根的意义，求满足条件的x值：（x﹣1）²＝36；

(2)、已知a＝2 $\sqrt{3}$ ﹣ $\sqrt{6}$ ，b＝2 $\sqrt{3} + \sqrt{6}$ ，求a²﹣ab的值．

查看试题解析
22. 《九章算术》是我国古代第一部数学专著，它的出现标志中国古代数学形成了完整的体系，“折竹抵地”问题源自《九章算术》中：“今有竹高一丈，去本四尺，问折者高几何？”翻译成数学问题是：如图所示，∠ACB＝90°，AC+AB＝10尺，BC=4尺，求AC的长．

查看试题解析
23. 如图所示，在平面直角坐标系中，已知A（2，2），B（1，0），C（3，﹣2）．

⑴请在平面直角坐标系中画出△ABC．

⑵请作△ABC关于y轴对称的△A′B′C′．

⑶已知点P为x轴上一点，若S_△_ABP＝5时，则点P的坐标为 ▲ ．

查看试题解析
24. 已知函数y＝(2m＋1)x＋m－3.

(1)、若函数图象经过原点，求m的值

(2)、若函数的图象平行于直线y＝3x－3，求m的值

(3)、若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围．

查看试题解析
25. “十一”期间，小华一家人开车到距家100千米的景点旅游，出发前，汽车油箱内储油35升，当行驶80千米时，发现油箱余油量为25升（假设行驶过程中汽车的耗油量是均匀的）

(1)、求该车平均每千米的耗油量；

(2)、写出剩余油量Q（升）与行驶路程x（千米）之间的关系式；

(3)、当油箱中剩余油量低于3升时，汽车将自动报警，如果往返途中不加油，他们能否在骑车报警前回家？请说明理由．

查看试题解析
26. [阅读材料]
把分母中的根号化去，使分母转化为有理数的过过程，叫做分母有理化．通常把分子、分母同时乘以同一个不等于0的数，以达到化去分母中根号的目的．

例如：化简 $\frac{1}{\sqrt{3} + \sqrt{2}}$ ．

解： $\frac{1}{\sqrt{3} + \sqrt{2}}$ ＝ $\frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) \times (\sqrt{3} - \sqrt{2})}$ ＝ $\sqrt{3}$ ﹣ $\sqrt{2}$ ．

[理解应用]

(1)、化简： $\frac{2}{\sqrt{5} + \sqrt{3}}$ ；

(2)、若a是 $\sqrt{2}$ 的小数部分，化简 $\frac{3}{a}$ ；

(3)、化简： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}}$ + $\frac{1}{\sqrt{7} + \sqrt{5}}$ +…+ $\frac{1}{\sqrt{2021} + \sqrt{2019}}$ ．

查看试题解析
27. 如图，直线l₁：y＝kx+1与x轴交于点D，直线l₂：y＝﹣x+b与x轴交于点A，且经过定点B（﹣1，5），直线l₁与l₂交于点C（2，m）．

(1)、求k、b和m的值；

(2)、求△ADC的面积；

(3)、在x轴上是否存在一点E，使△BCE的周长最短？若存在，请求出点E的坐标，请说明理由．

查看试题解析