江西省宜春市高安市2021-2022学年八年级上学期数学期中试卷
试卷更新日期：2021-12-22 类型：期中考试
一、单选题
-
1. 下面是科学防控新冠肺炎病毒传染的宣传图片，图片上有图案和文字说明，其中图案是轴对称图形的是（ ）A、
打喷嚏 捂口鼻
B、
喷嚏后 慎揉眼
C、
勤洗手 勤通风
D、
戴口罩 讲卫生
2. 已知三角形的一边长为6，则它的另两边长分别可以是（ ）A、6，6 B、3，3 C、2，3 D、6，123. 如图，点D在BC上，AB＝AD，∠B＝∠ADE，则补充下列条件，不一定能使△ABC≌△ADE的是（ ）
A、AC＝AE B、BC＝DE C、∠BAD＝∠CAE D、∠CDE＝∠CAE4. 如图，在△ABC中，以点B为圆心，以BA长为半径画弧交边BC于点D，连接AD．若∠B=40°，∠C=36°，则∠DAC的度数是（ ）
A、70° B、44° C、34° D、24°5. 如图，在△ABC中，∠C＝90°，AC＝2，∠B＝30°，点P是BC边上一动点，连接AP，则AP的长度不可能是（ ）
A、2 B、3 C、4 D、56. 定义：过△ABC的一个顶点作一条直线m，若直线m能将△ABC恰好分成两个等腰三角形，则称△ABC为“奇妙三角形”．如图，下列标有度数的四个三角形中，不是“奇妙三角形”的是（ ）A、
B、
C、
D、
二、填空题
-
7. 如图，活动衣架可以伸缩自如，是利用了四边形的 性质．
8. 如图，AC⊥BC，AD⊥BD，垂足分别是C、D，若要用“HL”得到Rt△ABC≌Rt△BAD，则你添加的条件是.（写一种即可）
9. 如图，正五边形ABCDE和正六边形EFGHMN的边CD、FG在直线l上，正五边形在正六边形左侧，两个正多边形均在l的同侧，则 的大小是度．
10. 如图，△ABC中，∠C=90°，AB=5，AC=4，BD平分∠ABC交AC于D，AD：DC=5：3，则△ABD的面积为 ．
11. 如图，AC平分∠DCB，CB＝CD，DA的延长线交BC于点E，若∠DAC＝125°，则∠BAE的度数为 ．
12. 如图，CA⊥AB，垂足为点A，AB=8cm，AC=4cm，射线BM⊥AB，垂足为点B，一动点E从A点出发，以2cm/秒的速度沿射线AN运动，点D为射线BM上一动点，随着E点运动而运动，且始终保持ED=CB，当点E运动秒时，点B、D、E组成的三角形与点A、B、C组成的三角形全等．
三、解答题
-
13. 如图
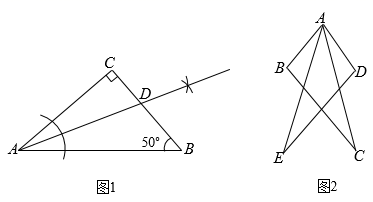(1)、如图1，△ABC中，∠C＝90°，∠B＝50°，根据图中尺规作图的痕迹，求∠ADC的度数．(2)、风筝为中国人发明，相传墨翟以木头制成木鸟，研制三年有成，是人类最早的风筝起源．如图2，小飞在设计的“风筝”图案中，已知AB＝AD，∠B＝∠D，∠BAE＝∠DAC，那么AC与AE相等吗？请说明理由．14. 已知，如图，D是△ABC的边AB上一点，AB∥FC，DF交AC于点E，DE＝EF．求证：AE＝CE．
15. 请仅用无刻度的直尺分别按下列要求画图（保留画图痕迹，不写画法）．
(1)、如图1，△ABC中，AB＝AC，点D，E分别在AB，AC边上，且AD＝AE，作出∠BAC(2)、如图2，四边形BCED中，BD＝CE，∠B＝∠C，M为BC边上一点，在BC边上作一点N，使CN＝BM．16. 如图，在△ABC中，∠B=∠C，过BC的中点D作DE⊥AB，DF⊥AC，垂足分别为点E、F.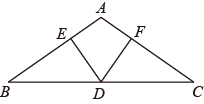
(1)、求证∶DE=DF；(2)、若∠BDE=55°，求∠BAC的度数.17. 如图，小聪想画∠AOB的角平分线，手头没有量角器和圆规，只有一个带刻度的直角三角尺，于是他按如下方法操作：在OA，OB边上量取OC＝OD＝1cm，分别过点C，点D作CF⊥OA，DE⊥OB，CF与DE交于点P，作射线OP，则射线OP就是∠AOB的角平分线．请判断小聪的做法是否可行？并说明理由．
18. 如图，在下列带有坐标系的网格中，△ABC的顶点都在边长为1的小正方形的顶点上，且点A的坐标为（﹣3，4）．
(1)、作出△ABC关于y轴对称的△DEF（点A与点D对应）；(2)、已知△ABC与△A′B′C′关于直线MN对称（点A与点A′对应），试作出直线MN；(3)、在（2）的条件下，观察△ABC与△A′B′C′各对对应点的坐标之间的关系，若Q（x，y）是△ABC内部任意一点，请直接写出这点在△A′B′C′内部的对应点Q′的坐标为 ．(4)、在（2）的条件下，在直线MN上作出一点P，使PB+PC的值最小，并简要描述作法．19. 已知△ABC三条边的长分别为：a+3，3a+1，a+5（a为正整数）．(1)、若△ABC是等腰三角形，求它的三边的长；(2)、若△ABC的三条边都不相等，求a的最小值．20. 如图，△ABC中，DM、EN分别垂直平分AB、AC边．
(1)、若∠B＝30°，∠C＝40°，求∠MAN的度数；(2)、若BC＝8cm，求△AMN的周长．21. 如图1，△ABE是等腰三角形，AB＝AE，∠BAE＝45°，过点B作BC⊥AE于点C，在BC上截取CD＝CE，连接AD、DE并延长AD交BE于点P；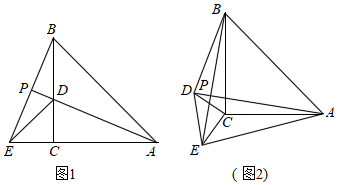
(1)、求证：AD＝BE；(2)、试说明AD平分∠BAE．(3)、如图2，将△CDE绕着点C旋转一定的角度，AD与BE交于点P，那么AD与BE的位置关系是否发生变化，说明理由．22. （问题背景）在学习了等腰三角形等有关知识后，数学活动小组对如图所示的课本上的一道例题进行了深入探究，发现：当角平分线遇上平行线时一般可得等腰三角形，有角平分线时，常过角平分线上一点作角的平行线构造等腰三角形．如图1，P为∠AOB的角平分线OC上一点，过点P作PD∥OB交OA于点D，易证△POD为等腰三角形．
(1)、（基本运用）如图2，把长方形纸片ABCD沿对角线AC折叠，点B落在点B'处，重合部分△ACE是等腰三角形吗？为什么？(2)、（类比探究）如图3，△ABC中，∠ABC的角平分线BO与外角∠ACG的角平分线交于点O，过点O作OD//BC分别交AB、AC于点D、点E，试探究线段BD、DE、CE之间的数量关系并说明理由；(3)、（拓展提升）如图4，四边形ABCD中，AD∥BC，E为CD边的中点，且AE平分∠BAD，连接BE，求证：AE⊥BE．23. 已知等边△ABC和射线AP，作AC边关于射线AP的对称线段AD，连接BD，CD．
(1)、如图1，当射线AP在∠BAC内部时，①请依题意补全图形；
②若∠PAC＝15°，则∠BDC＝ ▲ 度；
③若∠PAC＝x°，试求∠BDC的度数；
(2)、如图2，当射线AP在∠BAC外部的AC右侧时，设BD交AP于点E，①∠BDC＝ ▲ 度；
②线段AE，BE，DE之间有何数量关系？试说明理由．