黑龙江省齐齐哈尔市讷河市2021-2022学年八年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 下面各组线段中,能组成三角形的是( )A、1,2,3 B、1,2,4 C、3,4,5 D、4,4,82. 下列图形中不具有稳定性的是( )A、锐角三角形 B、长方形 C、直角三角形 D、等腰三角形3. △ABC和△DEF中,AB=DE,∠B=∠E,补充条件后仍不一定能保证△ABC≌△DEF,则补充的这个条件为( )A、BC=EF B、∠A=∠D C、AC=DF D、∠C=∠F4. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )A、4 B、5 C、6 D、75. 下列图形中被虚线分成的两部分不是全等图形的是( )A、
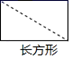 B、
B、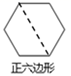 C、
C、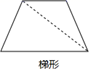 D、
D、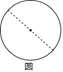 6. 如图,用尺规作图“过点C作CN//OA”的实质就是作∠DOM=∠NCE,其作图依据是( )
6. 如图,用尺规作图“过点C作CN//OA”的实质就是作∠DOM=∠NCE,其作图依据是( )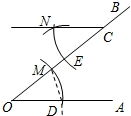 A、SAS B、SSS C、ASA D、AAS7. 如图所示,∠A+∠B+∠C+∠D+∠E的结果为( )
A、SAS B、SSS C、ASA D、AAS7. 如图所示,∠A+∠B+∠C+∠D+∠E的结果为( )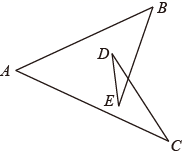 A、90° B、360° C、180° D、无法确定8. 正多边形的一个内角等于144°,则该多边形是( )A、正八边形 B、正九边形 C、正十边形 D、正十一边形9. 如图所示,BO,CO分别是∠ABC,∠ACB的两条角平分线,∠A=100°,则∠BOC的度数为( ).
A、90° B、360° C、180° D、无法确定8. 正多边形的一个内角等于144°,则该多边形是( )A、正八边形 B、正九边形 C、正十边形 D、正十一边形9. 如图所示,BO,CO分别是∠ABC,∠ACB的两条角平分线,∠A=100°,则∠BOC的度数为( ).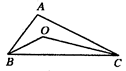 A、80° B、90° C、120° D、140°10. 如图所示, ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分别是E,F,下列结论:①DE=DF;②D是AC的中点;③E是AB的中点;④AB=BC+CD.其中正确的个数为( )
A、80° B、90° C、120° D、140°10. 如图所示, ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分别是E,F,下列结论:①DE=DF;②D是AC的中点;③E是AB的中点;④AB=BC+CD.其中正确的个数为( )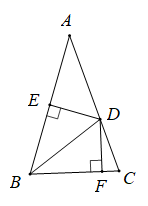 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
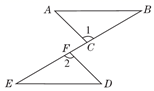
11. 已知三角形两边长分别为4和9,则第三边的取值范围是 .12. 已知在△ABC中,∠A=40°,∠B-∠C=40°,则∠B=.13. 如果一个多边形的内角和为1260°,那么从这个多边形的一个顶点可以连条对角线.14. 等腰三角形的周长为20cm,一条边长为6cm,则该等腰三角形的底边长为 .15. 如图,点C,F在线段BE上,BF=EC,∠1=∠2.请你添加一个条件,使△ABC≌△DEF,这个条件可以是(不再添加辅助线和字母).
 16. 如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则 BCD的面积为 .
16. 如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则 BCD的面积为 .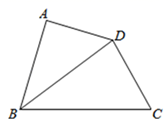 17. 如图,△ABD,△ACE都是等边三角形,BE和CD交于O点,则∠BOC=度.
17. 如图,△ABD,△ACE都是等边三角形,BE和CD交于O点,则∠BOC=度.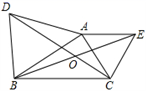
三、解答题
-
18. 如图
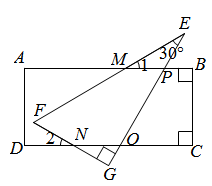 (1)、如图所示,直角三角板和直尺如图放置.若 ,试求出 的度数.(2)、已知 ABC的三边长a、b、c,化简 .19. 如图,已知AE=AC,AD=AB,∠1=∠2,
(1)、如图所示,直角三角板和直尺如图放置.若 ,试求出 的度数.(2)、已知 ABC的三边长a、b、c,化简 .19. 如图,已知AE=AC,AD=AB,∠1=∠2,求证:△EAD≌△CAB.
 20. 已知 ABC的两条高AD,BE相交于点H,且AD=BD.试解答下列问题:
20. 已知 ABC的两条高AD,BE相交于点H,且AD=BD.试解答下列问题: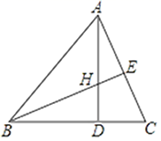 (1)、∠DBH与∠DAC相等吗?说明理由.(2)、BH与AC相等吗?说明理由.21. 在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D.
(1)、∠DBH与∠DAC相等吗?说明理由.(2)、BH与AC相等吗?说明理由.21. 在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D.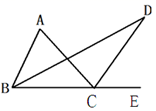 (1)、若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数.(2)、由(1)小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明.22. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE,BD相交于点O。
(1)、若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数.(2)、由(1)小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明.22. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE,BD相交于点O。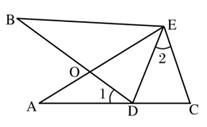 (1)、求证:△AEC≌△BED;(2)、若∠C=70°,求∠AEB的度数。23. 如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)、求证:△AEC≌△BED;(2)、若∠C=70°,求∠AEB的度数。23. 如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题: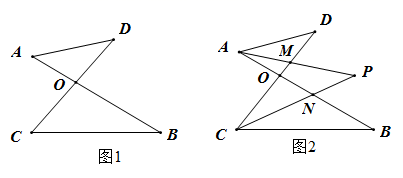 (1)、在图1中,请直接写出 之间的数量关系:﹔(2)、仔细观察,在图2中“8字形”的个数个;(3)、如果图2中,若 ,试求 的度数(4)、如果图2中, 和 为任意角,其他条件不变,试问 与 之间存在着怎样的数量关系(直接写出结论即可)24. 在△ABC中,D是BC边上的点(不与点B,C重合),连接AD.
(1)、在图1中,请直接写出 之间的数量关系:﹔(2)、仔细观察,在图2中“8字形”的个数个;(3)、如果图2中,若 ,试求 的度数(4)、如果图2中, 和 为任意角,其他条件不变,试问 与 之间存在着怎样的数量关系(直接写出结论即可)24. 在△ABC中,D是BC边上的点(不与点B,C重合),连接AD.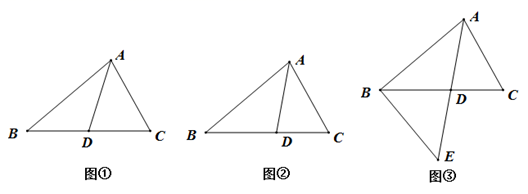 (1)、如图①,当D是BC中点时,则S△ABD:S△ACD= .(2)、如图②,当AD是∠BAC的平分线时求证:S△ABD:S△ACD=AB:AC.(3)、如图③,AD是∠BAC的平分线,延长AD到点E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,求△ABC的面积.
(1)、如图①,当D是BC中点时,则S△ABD:S△ACD= .(2)、如图②,当AD是∠BAC的平分线时求证:S△ABD:S△ACD=AB:AC.(3)、如图③,AD是∠BAC的平分线,延长AD到点E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,求△ABC的面积.