天津市滨海新区2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程 的两个根是( )A、 , B、 , C、 , D、 ,3. 用配方法解方程 ,配方后的方程是( )A、 B、 C、 D、4. 对于抛物线 ,下列说法正确的是( )A、开口向上,顶点坐标 B、开口向上,顶点坐标 C、开口向下,顶点坐标 D、开口向下,顶点坐标5. 将抛物线 向下平移2个单位,所得到的新抛物线的解析式为( )A、 B、 C、 D、6. 如图, 的直径为10,AB为弦, ,垂足为C,若OC=4,则弦AB的长为( )
2. 一元二次方程 的两个根是( )A、 , B、 , C、 , D、 ,3. 用配方法解方程 ,配方后的方程是( )A、 B、 C、 D、4. 对于抛物线 ,下列说法正确的是( )A、开口向上,顶点坐标 B、开口向上,顶点坐标 C、开口向下,顶点坐标 D、开口向下,顶点坐标5. 将抛物线 向下平移2个单位,所得到的新抛物线的解析式为( )A、 B、 C、 D、6. 如图, 的直径为10,AB为弦, ,垂足为C,若OC=4,则弦AB的长为( )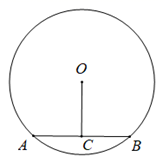 A、10 B、8 C、6 D、47. 如图,四边形ABCD为 的内接四边形,已知 ,则 的度数为( )
A、10 B、8 C、6 D、47. 如图,四边形ABCD为 的内接四边形,已知 ,则 的度数为( ) A、40° B、50° C、80° D、100°8. 如图,AB是 的直径,C,D是 上的两点,连接AC,CD,AD,若 ,则 的度数是( )
A、40° B、50° C、80° D、100°8. 如图,AB是 的直径,C,D是 上的两点,连接AC,CD,AD,若 ,则 的度数是( )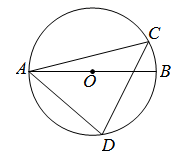 A、15° B、25° C、30° D、75°9. 如图,在 中, ,将 绕点 逆时针旋转得到 ,使点 的对应点 恰好落在边 上,点 的对应点为 ,延长 交 于点 ,则下列结论一定正确的是( )
A、15° B、25° C、30° D、75°9. 如图,在 中, ,将 绕点 逆时针旋转得到 ,使点 的对应点 恰好落在边 上,点 的对应点为 ,延长 交 于点 ,则下列结论一定正确的是( )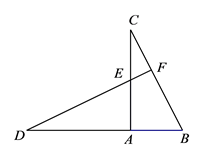 A、 B、 C、 D、10. 某种植基地2020年蔬菜产量为90吨,预计2022年蔬菜产量达到110吨,求蔬菜产量的年平均增长率.设蔬菜产量的年平均增长率为 ,则可列方程为( )A、 B、 C、 D、11. 如图,在 中, ,以点A为旋转中心,将 绕点A逆时针旋转得到 ,点B、C的对应点分别为D、E,连接CE,若 ,则 的大小是( )
A、 B、 C、 D、10. 某种植基地2020年蔬菜产量为90吨,预计2022年蔬菜产量达到110吨,求蔬菜产量的年平均增长率.设蔬菜产量的年平均增长率为 ,则可列方程为( )A、 B、 C、 D、11. 如图,在 中, ,以点A为旋转中心,将 绕点A逆时针旋转得到 ,点B、C的对应点分别为D、E,连接CE,若 ,则 的大小是( )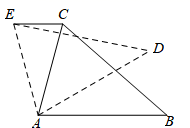 A、15° B、25° C、35° D、45°12. 如图,抛物线 与x轴交于点 ,其对称轴为直线 ,结合图象分析下列结论:① ;②当 时,y随x的增大而增大;③ ;④ ;⑤若m,n( )为方程 的两个根,则 且 .其中符合题意结论的个数是( )
A、15° B、25° C、35° D、45°12. 如图,抛物线 与x轴交于点 ,其对称轴为直线 ,结合图象分析下列结论:① ;②当 时,y随x的增大而增大;③ ;④ ;⑤若m,n( )为方程 的两个根,则 且 .其中符合题意结论的个数是( )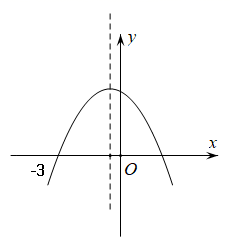 A、2个 B、3个 C、4个 D、5
A、2个 B、3个 C、4个 D、5二、填空题
-
13. 点 关于原点对称的点的坐标是 .14. 若关于 的一元二次方程 有两个实数根,则 的取值范围为 .15. 已知二次函数 的图象与 轴只有一个公共点,则此公共点的坐标是 .16. 已知抛物线y=ax2+bx+c=0(a≠0)与x轴交于A,B两点,若点A的坐标为(-1,0),抛物线的对称轴为直线x=2,则线段AB的长为 .17. 如图,四边形 内接于 , , , ,则 的值为 .
 18. 如图,在 中, , ,点D为 内一点, , ,连接AD,将 绕点C按逆时针方向旋转,使CA与CB重合,点D的对应点为点E,连接DE,DE交BC于点F,则BF的长为cm.
18. 如图,在 中, , ,点D为 内一点, , ,连接AD,将 绕点C按逆时针方向旋转,使CA与CB重合,点D的对应点为点E,连接DE,DE交BC于点F,则BF的长为cm.
三、解答题
-
19. 解下列方程(1)、 (配方法);(2)、 (公式法).20. 抛物线 的顶点为P,与 轴的交点为C.
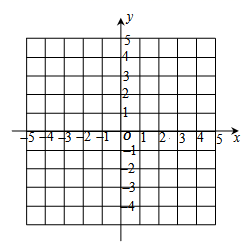 (1)、抛物线的对称轴是;顶点P的坐标是;交点C的坐标是 .(2)、列表、描点画这条抛物线.
(1)、抛物线的对称轴是;顶点P的坐标是;交点C的坐标是 .(2)、列表、描点画这条抛物线.…
…
…
…
21. 在 中, ,将 绕点C顺时针旋转,得 ,D,E分别是点B,A的对应点.记旋转角为 .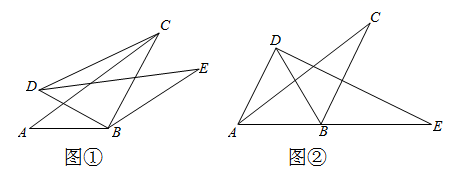 (1)、如图①,连接AD,若 , , ,求AD的长;(2)、如图②,连接BD,若 ,求证: .22. 已知 是 的内接三角形, 的平分线交 于点 .
(1)、如图①,连接AD,若 , , ,求AD的长;(2)、如图②,连接BD,若 ,求证: .22. 已知 是 的内接三角形, 的平分线交 于点 .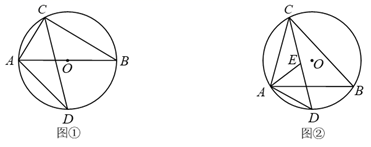 (1)、如图①,若 是 的直径, ,求 的长;(2)、如图②,若 的平分线交 于点 ,求证: .23. 商城某种商品平均每天可销售20件,每件获得利润40元,为庆元旦,决定对该商品进行促销活动,经调查发现,该商品每件每降价1元,平均每天可多售出2件.设该商品每件降价x元,请解答下列问题:(1)、用含x的代数式表示:
(1)、如图①,若 是 的直径, ,求 的长;(2)、如图②,若 的平分线交 于点 ,求证: .23. 商城某种商品平均每天可销售20件,每件获得利润40元,为庆元旦,决定对该商品进行促销活动,经调查发现,该商品每件每降价1元,平均每天可多售出2件.设该商品每件降价x元,请解答下列问题:(1)、用含x的代数式表示:①降价后每售一件该商品获得利润元;
②降价后平均每天售出件该商品;
(2)、在此次促销活动中,商城若要获得最大利润,每件该商品应降价多少元?此时每天获得最大利润为多少元?24. 在 中, , .(1)、如图,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC.求证:① ;
② .
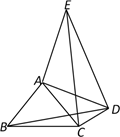
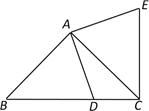 (2)、如图,D为 外一点,且 ,仍将线段AD绕点A逆时针旋转90°得到AE,连接EC,ED,BD.
(2)、如图,D为 外一点,且 ,仍将线段AD绕点A逆时针旋转90°得到AE,连接EC,ED,BD.① 的结论是否仍然成立?并请你说明理由;
②若 , ,求AD的长.
 25. 抛物线 与 轴交于 , 两点,与 轴交于点 ,抛物线的对称轴交 轴于点 ,已知 , .(1)、求抛物线的解析式;(2)、在抛物线的对称轴上是否存在点 ,使 是以 为腰的等腰三角形?如果存在,求出 点的坐标;如果不存在,请说明理由;(3)、点 是线段 上的一个动点,过点 作 轴的垂线与抛物线相交于点 ,当四边形 的面积最大时,求点 的坐标.
25. 抛物线 与 轴交于 , 两点,与 轴交于点 ,抛物线的对称轴交 轴于点 ,已知 , .(1)、求抛物线的解析式;(2)、在抛物线的对称轴上是否存在点 ,使 是以 为腰的等腰三角形?如果存在,求出 点的坐标;如果不存在,请说明理由;(3)、点 是线段 上的一个动点,过点 作 轴的垂线与抛物线相交于点 ,当四边形 的面积最大时,求点 的坐标.