山东省淄博市沂源县2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 二次函数y=a ,当a<0时,y的值恒小于0,则自变量x的取值范围( )A、x可取一切实数 B、x>0 C、x<0 D、x≠02. 已知二次函数
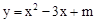 (m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程 的两实数根是( ) A、x1=1,x2=-1 B、x1=1,x2=2 C、x1=1,x2=0 D、x1=1,x2=33. 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程 的两实数根是( ) A、x1=1,x2=-1 B、x1=1,x2=2 C、x1=1,x2=0 D、x1=1,x2=33. 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )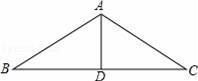 A、5sin36°米 B、5cos36°米 C、5tan36°米 D、10tan36°米4. 一个公共房门前的台阶高出地面1.2 m,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
A、5sin36°米 B、5cos36°米 C、5tan36°米 D、10tan36°米4. 一个公共房门前的台阶高出地面1.2 m,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )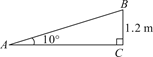 A、斜坡AB的坡度是10° B、斜坡AB的坡度是tan10° C、AC=1.2tan10° m D、AB= m5. 下列式子错误的是( )A、cos40°=sin50° B、tan15°•tan75°=1 C、sin225°+cos225°=1 D、sin60°=2sin30°6. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
A、斜坡AB的坡度是10° B、斜坡AB的坡度是tan10° C、AC=1.2tan10° m D、AB= m5. 下列式子错误的是( )A、cos40°=sin50° B、tan15°•tan75°=1 C、sin225°+cos225°=1 D、sin60°=2sin30°6. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )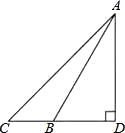 A、2 m B、2 m C、(2 ﹣2)m D、(2 ﹣2)m7. 二次函数的图象如图所示,则m的值是
A、2 m B、2 m C、(2 ﹣2)m D、(2 ﹣2)m7. 二次函数的图象如图所示,则m的值是 A、-8 B、8 C、±8 D、68. 已知二次函数y=2 ﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有 , , 三点满足 =m,则m的值是( )A、1 B、 C、2 D、49. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为( )人A、56 B、55 C、54 D、5310. 若二次函数 的图象与 轴有两个交点,坐标分别是(x1 , 0),(x2 , 0),且 . 图象上有一点 在 轴下方,则下列判断正确的是( )A、 B、 C、 D、11. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
A、-8 B、8 C、±8 D、68. 已知二次函数y=2 ﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有 , , 三点满足 =m,则m的值是( )A、1 B、 C、2 D、49. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为( )人A、56 B、55 C、54 D、5310. 若二次函数 的图象与 轴有两个交点,坐标分别是(x1 , 0),(x2 , 0),且 . 图象上有一点 在 轴下方,则下列判断正确的是( )A、 B、 C、 D、11. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是( )
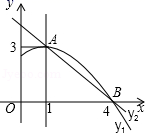 A、①②③ B、①③④ C、①③⑤ D、②④⑤12. △ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果 ,那么下列结论正确的是( )A、csinA= a B、b cosB=c C、a tanA= b D、ctanB= b
A、①②③ B、①③④ C、①③⑤ D、②④⑤12. △ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果 ,那么下列结论正确的是( )A、csinA= a B、b cosB=c C、a tanA= b D、ctanB= b二、填空题
-
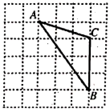
13. 若 是二次函数,且图象开口向下,则 的值为 .14. 在Rt△ABC中,AB是斜边,AB=10,BC=6,tanA= .15. 如图,在正方形网格中, 的顶点都在格点上,则 的值为 .
 16. 在平面直角坐标系中,将抛物线y= ﹣(a﹣2)x+ ﹣1向右平移4个单位长度,平移后的抛物线与y轴的交点为A(0,3),则平移后的抛物线的对称轴为 .17. 已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且﹣2≤x≤1时,y的最大值为9,则a的值为.
16. 在平面直角坐标系中,将抛物线y= ﹣(a﹣2)x+ ﹣1向右平移4个单位长度,平移后的抛物线与y轴的交点为A(0,3),则平移后的抛物线的对称轴为 .17. 已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且﹣2≤x≤1时,y的最大值为9,则a的值为.三、解答题
-
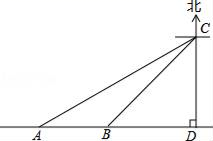
18. 计算:(1)、 cos30°+ sin45°;(2)、6tan230°﹣ sin 60°﹣2sin 45°.19. 已知抛物线y=x2﹣2x﹣15.(1)、求该抛物线的顶点坐标;(2)、求图象与x轴的交点坐标;(3)、当x取何值时,函数值大于0?20. 据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒.问此车是否超过了该路段16米/秒的限制速度?(参考数据: ≈1.4, ≈1.7)
 21. 如图,在Rt△ABC中,∠C=90°,sinB= ,D在BC边上,且∠ADC=45°,AC=5.求∠BAD的正切值.
21. 如图,在Rt△ABC中,∠C=90°,sinB= ,D在BC边上,且∠ADC=45°,AC=5.求∠BAD的正切值.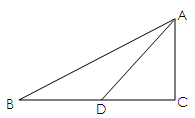 22. 如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y= x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为 m.
22. 如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y= x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为 m. (1)、求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(1)、求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)、一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)、在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
23. 在平面直角坐标系中,抛物线 的顶点为A .(1)、求顶点A的坐标(用含有字母m的代数式表示);(2)、若点 , 在抛物线上,且 ,则m的取值范围是;(直接写出结果即可)(3)、当 时,函数y的最小值等于6,求m的值.24. 如图,抛物线y=x2+bx+c交x轴于A(﹣ ,0)、B两点,交y轴于点C(0,﹣3),点D是线段BC下方的抛物线上一个动点,过点D作DE⊥x轴于点E,交线段BC于点F.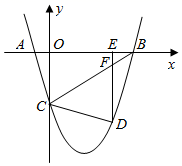 (1)、求抛物线的表达式;(2)、求△BCD面积的最大值,并写出此时点D的坐标.(3)、是否存在点D,使得△CDF与△BEF相似,若存在,求出点D的坐标,若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、求△BCD面积的最大值,并写出此时点D的坐标.(3)、是否存在点D,使得△CDF与△BEF相似,若存在,求出点D的坐标,若不存在,请说明理由.