山东省泰安市泰山区2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. $\tan 60 °$ 的值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、1 D、 $\sqrt{3}$

查看试题解析
2. 下列函数不是反比例函数的是（）

A、y＝ $- \frac{3}{2 x}$ B、y＝ $- \frac{x}{5}$ C、y＝5x^﹣1 D、xy＝10

查看试题解析
3. 对于反比例函数y＝- $\frac{6}{x}$ ，下列说法正确的是（）

A、图象经过点（﹣2，﹣3） B、图象位于第一、三象限 C、当x＞0时，y随x的增大而减小 D、当x＜0时，y随x的增大而增大

查看试题解析
4. 关于二次函数y＝﹣3（x﹣1）²+5，下列说法正确的是（）

A、其图象的开口向上 B、其图象的对称轴为直线x＝﹣1 C、当x＜1时，y随x的增大而增大 D、其最小值为5

查看试题解析
5. 如果等腰三角形的面积为6，底边长为x，底边上的高为y，则y与x的函数关系式为（）

A、y＝ $\frac{12}{x}$ B、y＝ $\frac{x}{12}$ C、y＝ $\frac{6}{x}$ D、y＝ $\frac{3}{x}$

查看试题解析
6. 在Rt△ABC中，有下列情况，则直角三角形可解的是（）

A、已知BC＝6，∠C＝90° B、已知∠C＝90°，∠A＝60°，BC＝5 C、已知∠C＝90°，∠A＝∠B D、已知∠C＝∠B＝45°

查看试题解析
7. 把抛物线y＝ $\frac{1}{2}$ （x﹣1）²+3向左平移3个单位长度，再向下平移4个单位长度，得到的抛物线表达式为（）

A、y＝ $\frac{1}{2}$ （x﹣4）²﹣1 B、y＝ $\frac{1}{2}$ （x﹣4）²+7 C、y＝ $\frac{1}{2}$ （x+2）²﹣1 D、y＝ $\frac{1}{2}$ （x+2）²+7

查看试题解析
8. 已知二次函数y＝（m﹣1）x²+3x﹣1与x轴有交点，则m的取值范围是（）

A、m $> - \frac{5}{4}$ B、m $\geq - \frac{5}{4}$ C、m $> - \frac{5}{4}$ 且m≠1 D、m $\geq - \frac{5}{4}$ 且m≠1

查看试题解析
9. 在同一平面直角坐标系中，反比例函数y＝ $- \frac{k}{x}$ （k≠0）与二次函数y＝x²﹣kx﹣k的大致图象是（）

A、 B、 C、 D、

查看试题解析
10. 如图，一次函数y=－x与二次函数y=ax²+bx+c的图象相交于点M、N，则关于x的一元二次方程ax²+(b+1)x+c=0的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、以上结论都符合题意

查看试题解析
11. 如图，A、B是第二象限内双曲线y＝ $\frac{k}{x}$ 上的点，A、B两点的横坐标分别是a，3a，线段AB的延长线交x轴于点C，S_△AOC＝12．则k的值为（）

A、﹣6 B、﹣5 C、﹣4 D、﹣3

查看试题解析
12. 二次函数y＝ax²+bx+c的图象如图所示，对称轴是直线x＝1．下列结论：①b＞0；②当x＞0，y随着x的增大而增大；③（a+c）²﹣b²＜0；④a+b≥m（am+b）（m为实数）．其中结论正确的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

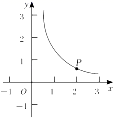
13. 在△ABC中，若∠C＝90°，sinA＝ $\frac{\sqrt{5}}{5}$ ，则tanA＝．

查看试题解析
14. 若二次函数y＝ $m x^{m^{2} - m}$ 的图象开口向上，则m＝．

查看试题解析
15. 抛物线y＝﹣x²﹣4x+m﹣1，若其顶点在x轴上，则m＝．

查看试题解析
16. 如图，点P在反比例函数y＝ $\frac{1}{x}$ （x＞0）的图象上，且横坐标为2．若将点P先向右平移2个单位，再向上平移2个单位后所得图象为点P′．则经过点P′的反比例函数图象的关系式是．

查看试题解析
17. 如图，矩形ABCD的顶点D在反比例函数y＝ $\frac{k}{x}$ （x＜0）的图象上，顶点B、C在x轴上，对角线AC的延长线交y轴于点E，连接BE，若△BCE的面积是4，则k的值为．

查看试题解析
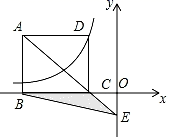18. 如图，在x轴正半轴上依次截取OA₁＝A₁A₂＝A₂A…A_n_﹣1A_n（n为正整数），过点A₁、A₂、A₃、…、A_n分别作x轴的垂线，与反比例函数y＝ $\frac{1}{x}$ （x＞0）交于点P₁、P₂、P₃、…、P_n ，连接P₁P₂、P₂P₃、…、P_n_﹣1P_n ，过点P₂、P₃、…、P_n分别向P₁A₁、P₂A₂、…、P_n_﹣1A_n_﹣1作垂线段，构成的一系列直角三角形（见图中阴影部分）的面积和是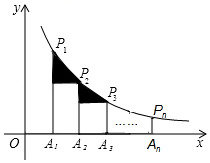

查看试题解析

三、解答题

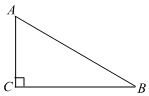
19. 如图，在Rt△ABC中，∠C＝90°，BC＝2，AC＝2 $\sqrt{3}$ ．解这个直角三角形．

查看试题解析
20. 如图，在平面直角坐标系中．四边形 $O A B C$ 为矩形，点 $C$ 、 $A$ 分别在 $x$ 轴和 $y$ 轴的正半轴上，点 $D$ 为 $A B$ 的中点已知实数 $k \neq 0$ ，一次函数 $y = - 3 x + k$ 的图像经过点 $C$ 、 $D$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图像经过点 $B$ ，求 $k$ 的值．

查看试题解析
21. 已知二次函数y＝x²+bx+c的图象经过点A（﹣2，﹣3）和点B（2，5）．

(1)、求这个二次函数的关系式；

(2)、求这个函数图象的顶点坐标；

(3)、在所给坐标系中画出这个函数的图象．

查看试题解析
22. 在学习解直角三角形以后，数学兴趣小组测量了学校旗杆的高度．如图，某一时刻，旗杆AB的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为4米，落在斜坡上的影长CD为3.8米，AB⊥BC，同一时刻，光线与水平面的夹角为60°，1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆的高度（结果精确到0.1米，参考数据： $\sqrt{3}$ ≈1.732）．

查看试题解析
23. 已知A（﹣3，4），B（n，﹣2）是一次函数y＝kx+b的图象和反比例函数y＝ $\frac{m}{x}$ 的图象的两个交点，直线AB与x轴交于点C．

(1)、求反比例函数和一次函数的关系式；

(2)、连接OB，求△AOB的面积．

查看试题解析
24. 某景区超市销售一种纪念品，这种商品的成本价15元/件，已知销售价不低于成本价，且物价部门规定这种商品的销售价不高于24元/件，市场调查发现，该商品每天的销售量y（件）与销售单价x（元/件）之间的函数关系如图所示．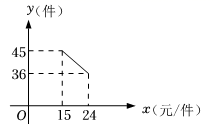

(1)、求y与x之间的函数关系式，并写出自变量x的取值范围；

(2)、求每天的销售利润W（元）与销售单价x（元/件）之间的函数关系式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？

查看试题解析
25. 如图，抛物线y＝﹣x²+bx+c与x轴相交于A、B两点，与y轴相交于点C ，且点B与点C的坐标分别为B(3，0)，C(0，3)，点M是抛物线的顶点．

(1)、求二次函数的关系式；

(2)、点P为线段MB上一个动点，过点P作PD⊥x轴于点D ．若OD＝m ， △PCD的面积为S ，
①求S与m的函数关系式，写出自变量m的取值范围．

②当S取得最值时，求点P的坐标；

(3)、在MB上是否存在点P ，使△PCD为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．

查看试题解析