山东省德州市庆云县2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列关于x的方程中，是一元二次方程的为（）

A、（a﹣1）x²﹣2＝0 B、x²+ $\frac{2}{x}$ ＝﹣1 C、x²﹣4＝2y D、﹣2x²+3＝0

查看试题解析
2. 下列4个图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 把方程 $x^{2} - 4 x - 7 = 0$ 化成 ${(x - m)}^{2} = n$ 的形式，下列变形确的是（）

A、 ${(x - 2)}^{2} = 3$ B、 ${(x - 2)}^{2} = 11$ C、 ${(x - 4)}^{2} = 11$ D、 ${(x + 2)}^{2} = 11$

查看试题解析
4.
在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M₁N₁P₁ ，则其旋转中心可能是（　　）

A、点A B、点B C、点C D、点D

查看试题解析
5. 将抛物线y＝2（x﹣1）²﹣3向右移动2个单位，再向下移动3个单位，得到的抛物线的解析式为（）

A、y＝2（x+1）² B、y＝2（x+1）²﹣6 C、y＝2（x﹣3）² D、y＝2（x﹣3）²﹣6

查看试题解析
6. 已知OA=4，以O为圆心，r为半径作⊙O.若使点A在⊙O内，则r的值可以是（　）

A、2 B、3 C、4 D、5

查看试题解析
7. 关于二次函数 $y = x^{2} - 2 x - 3$ ，下列说法错误的是（）

A、顶点坐标为 $(1 ， - 4)$ B、对称轴为 $x = 1$ C、抛物线与 $x$ 轴有两个交点 D、 $x = 2$ 与 $x = - 2$ 时函数值一样大

查看试题解析
8. 如图， $⊙ O$ 是 $Δ A B C$ 的外接圆， $∠ B A C = 60 °$ ，若 $⊙ O$ 的半径 $O C$ 为2，则弦 $B C$ 的长为（）

A、4 B、 $2 \sqrt{3}$ C、3 D、 $\sqrt{3}$

查看试题解析
9. 如图，直线 $y_{1} = k x$ 与抛物线 $y_{2} = a x^{2} + b x + c$ 交于 $A$ 、 $B$ 两点，则 $y = a x^{2} + (b - k) x + c$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 骑行带头盔，安全有保障．“一盔一带”政策的推行致头盔销量大幅增长，从2018年到2020年我国头盔销售额从18亿元增长到30.42亿元，则我国头盔从2018年到2020年平均每年增长率是（）

A、10% B、20% C、30% D、40%

查看试题解析
11. 如图，在⊙O中，AB为直径，点M为AB延长线上的一点，MC与⊙O相切于点C，圆周上有另一点D与点C分居直径AB两侧，且使得MC＝MD＝AC，连接AD．现有下列结论：①MD与⊙O相切；②四边形ACMD是菱形；③AB＝MO；④∠ADM＝120°，其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
12. 已知二次函数y＝ax²+bx+c的y与x的部分对应值如下表：

x

﹣2

﹣1

0

1

3

y

5

0

﹣3

﹣4

0

下列结论：①抛物线开口向上；②抛物线对称轴为直线x＝1；③ax²+bx+c＝5的另一个解是x＝4；④当﹣1＜x＜3时，y＞0；⑤抛物线与x轴的两个交点间的距离是4，其中，正确的个数（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 请写出一个开口向上，且经过点（0，-1）的抛物线解析式：
（只需写一个）

查看试题解析
14. 如图，A、B是⊙O上的两点，AC是过点A的一条直线，如果∠AOB＝120°，那么当∠CAB＝时，AC与⊙O相切．

查看试题解析
15. 已知a，b是一元二次方程2x²+2x﹣2021＝0的两个实数根，则代数式2a²+3a+b＝．

查看试题解析
16. 如图所示：在△ABC中，将△ABC绕点A顺时针旋转得到△ADE点B的对应点D恰好落在BC边上，∠B＝55°，则∠EDC的度数是．

查看试题解析
17. 如图，在Rt△ABC中，∠B＝90°，AB＝6cm，BC＝8cm，点P从A点开始沿AB边向点B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动，则P、Q分别从A、B同时出发，经过秒钟，使△PBQ的面积最大．

查看试题解析
18. 如图所示，AB是⊙O的直径，AD、BC是⊙O的两条切线，E、F分别在AD、BC上，EF切⊙O于点G，连接OE、OF、BG、AG，BG与OF相交于点M，AG与OE相交于点N，已知AE＝2，BF＝8．以下结论：①⊙O的半径为2；②AG∥OF；③BG＝ $\frac{16 \sqrt{5}}{5}$ ；④四边形OMGN是正方形．其中正确的结论有（填序号）．

查看试题解析

三、解答题

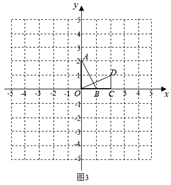
19.

(1)、2﹣x＝3x（x﹣2）；

(2)、x²﹣2x﹣3＝0（配方法）．

查看试题解析
20. 如图，在平面直角坐标系xOy中，△AOB可以看作是△OCD经过若干次图形的变化（平移、轴对称、旋转）得到的，按照下列要求写出三种由△OCD得到△AOB的过程且画出图形．例如：（平移和旋转）△OCD向上平移两个单位后，再绕点A顺时针旋转90°后与△AOB重合．如图．方法一：如图1，写出经过旋转和轴对称变化的过程且画出图形．方法二：如图2，写出经过旋转变化的过程且画出图形．方法三：如图3，写出经过轴对称变化的过程且画出图形．

查看试题解析
21. 要修一个圆形喷水池，在池中心竖直安装一根水管，水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m ，水柱落地处离池中心3m ，水管应多长？

查看试题解析
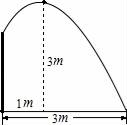22. 如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆⊙O相交于点D过D作直线DG∥BC．

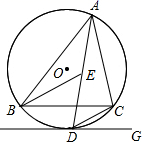(1)、若∠ACB＝70°，则∠ADB＝；∠AEB＝．

(2)、求证：DE＝CD；

(3)、求证：DG是⊙O的切线．

查看试题解析
23. 某商店销售一种销售成本为40元/千克的水产品，若按50元/千克销售，一个月可售出500千克，销售价每涨价1元，月销售量就减少10千克.

(1)、写出月销售利润y（单位：元）与售价x（单位：元/千克）之间的函数关系式.

(2)、商场将在月销售成本不超过3000元的情况下，使得月销售利润达到8000元，销售单价应定为多少？

(3)、当售价定为多少元时，会获得最大利润？求出最大利润.

查看试题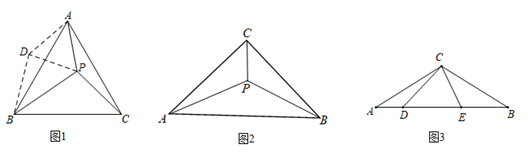解析
24. 如图

（阅读材料）（1）在某次数学兴趣小组活动中，小明同学遇到了如下问题：如图1，在等边△ABC中，点P在内部，且PA＝3，PC＝4，∠APC＝150°，求PB的长．经过同学们的观察、分析、思考、交流，对上述问题形成了如下想法：将△APC绕点A按顺时针方向旋转60°，得到△ABD，连接PD，寻找PA、PB、PC三边之间的数量关系．即能求PB＝请参考他们的想法，完成下面问题：

查看试题解析
25. 如图，抛物线y＝ax²+bx+c与x轴的两个交点为A、B，且当x＜﹣1时，y随x的增大而减小，x＞﹣1时，y随x的增大而增大，其最小值为﹣ $\frac{12}{5}$ ，其图象与x轴的交点B的横坐标是1，过点B的直线l：y＝kx+ $\frac{3}{5}$ 分别与y轴及抛物线交于点C，D．

(1)、求直线l和抛物线的解析式；

(2)、过点D作x轴的平行线交抛物线于点E，点P是直线DE上的一个动点，点D关于直线OP的对称点F恰好在y轴上，求直线OP的解析式．

(3)、将（1）中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方图象的其余部分保持不变，翻折后的图象与原图象x轴上方的部分组成一个“W”形状的新图象，将直线平移得到直线l，若直线l与该新图象恰好有三个公共点，请求出上下平移了几个单位长度．

查看试题解析

x	﹣2	﹣1	0	1	3
y	5	0	﹣3	﹣4	0