山东省德州市陵城区2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列y关于x的函数中，属于二次函数的是（　　）

A、y＝（x+1）²﹣x² B、y＝ax²+bx+c C、y＝3x²﹣1 D、y＝3x﹣1

查看试题解析
2. 下列疫情防控标识图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，AB是⊙O的直径，CD是⊙O的弦，如果∠ACD＝36°，那么∠BAD等于（）

A、36° B、44° C、54° D、56°

查看试题解析
4. 直线 $y = x + 2 m$ 经过第一、三、四象限，则抛物线 $y = x^{2} + 2 x + 1 - m$ 与 $x$ 轴的交点个数为（）

A、0个 B、1个 C、2个 D、1个或2个

查看试题解析
5. 某地要建造一个圆形喷水池，在水池中央垂直于地面安装一个柱子 $O A ， O$ 恰为水面中心，安置在柱子顶端 $A$ 处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，在过 $O A$ 的任一平面上，建立平面直角坐标系（如图），水流喷出的高度 $y (m)$ 与水平距离 $x (m)$ 之间的关系式是 $y = - x^{2} + 2 x + 3$ ，则下列结论错误的是（）

A、柱子 $O A$ 的高度为 $3 m$ B、喷出的水流距柱子 $1 m$ 处达到最大高度 C、喷出的水流距水平面的最大高度是 $3 m$ D、水池的半径至少要 $3 m$ 才能使喷出的水流不至于落在池外

查看试题解析
6. 如图，四边形 $A B C D$ 内接于圆 $O$ ，过 $B$ 点作 $B H ⊥ A D$ 于点 $H$ ，若 $∠ B C D = 135^{\circ}$ ， $A B = 4$ ，则 $B H$ 的长度为（）

A、 $\sqrt{2}$ B、 $2 \sqrt{2}$ C、 $3 \sqrt{2}$ D、不能确定

查看试题解析
7. 如图，在△ABC中，∠CAB＝30°，将△ABC在平面内绕点A逆时针旋转到△AB'C'的位置，且CC'∥AB，则旋转角的度数为（）

A、100° B、120° C、110° D、130°

查看试题解析
8. 若⊙P的半径为4，圆心P的坐标为（-3，4），则平面直角坐标系的原点O与⊙P的位置关系是（）

A、在⊙P内 B、在⊙P上 C、在⊙P外 D、无法确定

查看试题解析
9. 如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD＝8cm，AE＝2cm，则△OFC的面积是（）

A、40cm² B、20cm² C、10cm² D、5cm²

查看试题解析
10. 已知二次函数y＝﹣ $x^{2}$ +bx+c的图象经过（﹣1，0）与（5，0）两点，且关于x的方程﹣x²+bx+c+d＝0有两个根，其中一个根是6，则d的值为（）

A、5 B、7 C、12 D、﹣7

查看试题解析
11. 如图，AB是⊙O的直径，弦MN∥AB，分别过M，N作AB的垂线，垂足为C，D．以下结论：①AC＝BD；② $\overset{⌢}{A M} = \overset{⌢}{B N}$ ；③若四边形MCDN是正方形，则MN＝ $\frac{1}{2}$ AB；④若M为 $\overset{⌢}{A N}$ 的中点，则D为OB中点；所有正确结论的序号是（）

A、①②③ B、①②④ C、①② D、①②③④

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的一部分如图所示，顶点坐标为 $(- 1 ， m)$ ，与x轴的一个交点的坐标为 $(- 3 ， 0)$ ，给出以下结论：① $a b c > 0$ ；② $4 a - 2 b + c > 0$ ；③若 $B (- \frac{5}{2} ， y_{1})$ 、 $C (- \frac{1}{2} ， y_{2})$ 为函数图象上的两点，则 $y_{1} < y_{2}$ ；④当-3 $<$ $x$ $<$ 0时方程 $a x^{2} + b x + c = t$ 有实数根，则t的取值范围是 $0 < t \leq m$ ，其中正确的结论的个数为（）

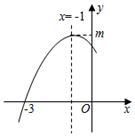A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

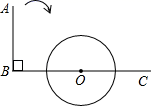
13. 若y＝（m﹣4）x^|m|^﹣2﹣2x﹣1是关于x的二次函数，则m＝．

查看试题解析
14. 若点A（2m﹣1，2n+5）与点B（4﹣m，1+m）关于原点O对称，则m＝， n＝．

查看试题解析
15. 在平面直角坐标系中，已知A（﹣1，m）和B（5，m）是抛物线y＝x²＋bx＋1上的两点，b＝；m＝；将抛物线y＝x²＋bx＋1的图象向上平移n（n是正整数）个单位，使平移后的图象与x轴没有交点，则n的最小值为．

查看试题解析
16. 如图，∠ABC＝90°，O为射线BC上点，以点O为圆心， $\frac{1}{2}$ BO长为半径作⊙O，当射线BA绕点B按顺时针方向旋转度时与⊙O相切．

查看试题解析
17. 如图，在正方形ABCD中，AB=8，点M在CD边上，且DM=2，△AEM与△ADM关于AM所在直线对称，将△ADM按顺时针方向绕点A旋转90°得到△ABF，连接EF，则线段EF的长为．

查看试题解析
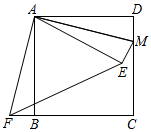18. 如图，P是抛物线y＝x²﹣2x﹣3在第四象限的一点，过点P分别向x轴和y轴作垂线，垂足分别为A、B，则四边形OAPB周长的最大值为．

查看试题解析

三、解答题

19. 已知抛物线C：y＝（x﹣m）²+m+1．

(1)、若抛物线C的顶点在第二象限，求m的取值范围；

(2)、若m＝﹣2，求抛物线C与坐标轴的交点围成的三角形的面积．

查看试题解析
20. 在如图所示的网格中建立平面直角坐标系，△ABC的顶点在网格线的交点上，点B的坐标为（﹣1，﹣1）．

(1)、画出△ABC向上平移4个单位长度得到的△A₁B₁C₁ ，并写出点B的对应点B₁的坐标；

(2)、画出△A₁B₁C₁绕原点O顺时针旋转90°得到的△A₂B₂C₂ ，并写出点B₁的对应点B₂的坐标．

查看试题解析
21. 如图，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于点E、D，连接ED、BE.

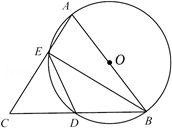(1)、试判断DE与DC是否相等，并说明理由；

(2)、如果BD＝2 $\sqrt{6}$ ，AE＝2，求⊙O的直径.

查看试题解析
22. 如图， $Δ A B C$ 逆时针旋转一定角度后与 $Δ A D E$ 重合，且点C在AD上.

(1)、指出旋转中心；

(2)、若 $∠ B = 21^{°}$ ， $∠ A C B = 26^{°}$ ，求出旋转的度数；

(3)、若 $A B = 5$ ， $C D = 3$ ，则AE的长是多少？为什么？

查看试题解析
23. 在平面直角坐标系中，设二次函数y₁＝ax²+2x+c，y₂＝cx²+2x+a（a，c是实数且ac≠0）．

(1)、若函数y₁的对称轴是直线x＝1且函数y₁的图象经过点（0，3），求函数y₁的表达式．

(2)、在（1）的条件下，当﹣1≤x≤0时，y₂的取值范围．

(3)、设函数y₁和函数y₂的最大值分别为m和n．若m+n＝0，探究实数a，c满足的关系式．

查看试题解析
24. 国庆期间，某商场销售一种商品，进货价为20元/件，当售价为24元/件时，每天的销售量为200件，在销售的过程中发现：销售单价每上涨1元，每天的销量就减少10件．设销售单价为x（元/件）（x≥24），每天销售利润为y（元）．

(1)、直接写出y与x的函数关系式为：；

(2)、若要使每天销售利润为1400元，求此时的销售单价；

(3)、若每件小商品的售价不超过36元，求该商场每天销售此商品的最大利润．

查看试题解析
25. 如图，抛物线y＝ax² $+ \frac{9}{4}$ 经过△ABC的三个顶点，点A坐标为（﹣1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．

(1)、求该抛物线的函数关系表达式；

(2)、点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F点的坐标．

查看试题解析