内蒙古自治区呼和浩特市2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 下列图形既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程中,一元二次方程是( )A、2x+1=0 B、 C、x2﹣3=0 D、x﹣2y=03. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )
2. 下列方程中,一元二次方程是( )A、2x+1=0 B、 C、x2﹣3=0 D、x﹣2y=03. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )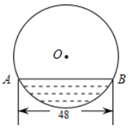 A、 B、 C、 D、4. 将抛物线y=x2向上平移4个单位长度,再向右平移1个单位长度后,得到的抛物线的解析式为( )A、y=(x+1)2+4 B、y=(x﹣1)2+4 C、y=(x+4)2﹣1 D、y=(x﹣4)25. 已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )A、1 B、7 C、4或3 D、7或16. 函数y=ax2﹣a与y=ax﹣a(a≠0)在同一坐标系中的图象可能是( )A、
A、 B、 C、 D、4. 将抛物线y=x2向上平移4个单位长度,再向右平移1个单位长度后,得到的抛物线的解析式为( )A、y=(x+1)2+4 B、y=(x﹣1)2+4 C、y=(x+4)2﹣1 D、y=(x﹣4)25. 已知AB,CD是⊙O的两条平行弦,AB=8,CD=6,⊙O的半径为5,则弦AB与CD的距离为( )A、1 B、7 C、4或3 D、7或16. 函数y=ax2﹣a与y=ax﹣a(a≠0)在同一坐标系中的图象可能是( )A、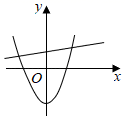 B、
B、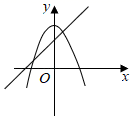 C、
C、 D、
D、 7. 如下图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
7. 如下图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )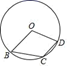 A、96° B、98° C、102° D、100°8. 已知a是一元二次方程x2﹣3x﹣5=0的较小的根,则下面对a的估计正确的是( )A、﹣2<a<﹣1 B、2<a<3 C、﹣4<a<﹣3 D、4<a<59. 如图, 是 的外接圆,半径 , ,则弦 的长为( )
A、96° B、98° C、102° D、100°8. 已知a是一元二次方程x2﹣3x﹣5=0的较小的根,则下面对a的估计正确的是( )A、﹣2<a<﹣1 B、2<a<3 C、﹣4<a<﹣3 D、4<a<59. 如图, 是 的外接圆,半径 , ,则弦 的长为( )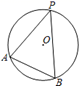 A、 B、2 C、2 D、410. 如图,二次函数y=ax2+bx+c(a 0)的图象过点(-2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1 , m),B(x2 , m)是抛物线上的两点,当x=x1+x2时,y=c;④若方程a(x+2)(4-x)=-2的两根为x1 , x2 , 且x1<x2 , 则-2 x1<x2<4.
A、 B、2 C、2 D、410. 如图,二次函数y=ax2+bx+c(a 0)的图象过点(-2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1 , m),B(x2 , m)是抛物线上的两点,当x=x1+x2时,y=c;④若方程a(x+2)(4-x)=-2的两根为x1 , x2 , 且x1<x2 , 则-2 x1<x2<4.其中结论正确的有( )
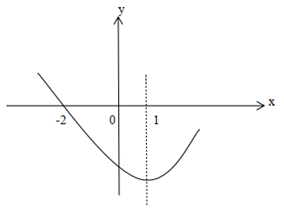 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 将点P(-2,3)向右平移3个单位得到点P1 , 点P2与点P1关于原点对称,则P2的坐标是12. 抛物线的形状大小、开口方向都与y=﹣12x2相同且顶点为(1,﹣2),则该抛物线的解析式为 .13. 某种药品连续两次降价后,由每盒200元下调到每盒128元,这种药品每次降价的百分率为 .14. 如图,点P(x,y)在抛物线y=﹣(x﹣1)2+2的图象上,若﹣1<x<2,则y的取值范围是 .
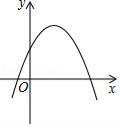 15. 如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为 则正方形ABCD的面积为
15. 如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为 则正方形ABCD的面积为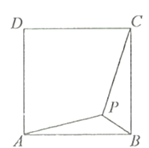 16. 已知二次项系数等于1的一个二次函数,其图象与x轴交于两点(m,0),(n,0),且过A(0,b),B(3,a)两点(b,a是实数),若0<m<n<2,则ab的取值范围是 .
16. 已知二次项系数等于1的一个二次函数,其图象与x轴交于两点(m,0),(n,0),且过A(0,b),B(3,a)两点(b,a是实数),若0<m<n<2,则ab的取值范围是 .三、解答题
-
17. 用适当的方法解下列方程.(1)、x2﹣3x+1=0;(2)、(x+4)2=5(x+4);18. 已知 、 是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根.(1)、试确定m的取值范围;(2)、当 时,求m的值.19. 如图,一位篮球运动员跳起投篮,球沿抛物线y=﹣ x2+3.5运行,然后准确落入篮框内.已知篮框的中心离地面的距离为3.05米.
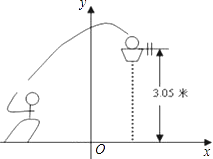 (1)、球在空中运行的最大高度为多少米?(2)、如果该运动员跳投时,球出手离地面的高度为2.25米,请问他距离篮框中心的水平距离是多少?20. 分别画出 绕点 逆时针旋转 和 后的图形.
(1)、球在空中运行的最大高度为多少米?(2)、如果该运动员跳投时,球出手离地面的高度为2.25米,请问他距离篮框中心的水平距离是多少?20. 分别画出 绕点 逆时针旋转 和 后的图形.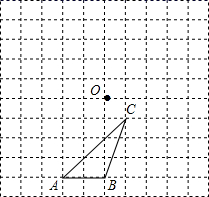 21. 某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示:
21. 某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示: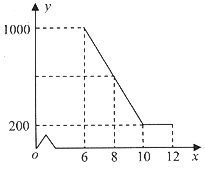 (1)、求y与x的函数解析式(也称关系式);(2)、求这一天销售西瓜获得的利润的最大值.22. 如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
(1)、求y与x的函数解析式(也称关系式);(2)、求这一天销售西瓜获得的利润的最大值.22. 如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.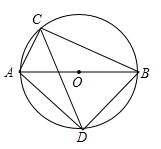 23. 已知等边△ABC,点D为BC上一点,连接AD.
23. 已知等边△ABC,点D为BC上一点,连接AD.
图1 图2
(1)、若点E是AC上一点,且CE=BD,连接BE,BE与AD的交点为点P,在图(1)中根据题意补全图形,直接写出∠APE的大小;(2)、将AD绕点A逆时针旋转120°,得到AF,连接BF交AC于点Q,在图(2)中根据题意补全图形,用等式表示线段AQ和CD的数量关系,并证明.24. 已知抛物线(1)、通过配方可以将其化成顶点式为 , 根据该抛物线在对称轴两侧从左到右图象的特征,可以判断,当顶点在x轴(填上方或下方),即 0(填大于或小于)时,该抛物线与x轴必有两个交点;(2)、若抛物线上存在两点 , ,分布在x轴的两侧,则抛物线顶点必在x轴下方,请你结合A、B两点在抛物线上的可能位置,根据二次函数的性质,对这个结论的符合题意性给以说明;(为了便于说明,不妨设 且都不等于顶点的横坐标;另如果需要借助图象辅助说明,可自己画出简单示意图)(3)、利用二次函数(1)(2)结论,求证:当 , 时, .