辽宁省大连市甘井子区2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四种图形既是中心对称图形又是轴对称图形的是（）

A、等腰三角形 B、等边三角形 C、平行四边形 D、矩形

查看试题解析
2. 将方程x（x﹣1）＝5（x+2）化成ax²+bx+c＝0的形式，则a，b，c的值分别为（）

A、1，6，10 B、1，﹣6，﹣10 C、1，﹣6，10 D、1，6，﹣10

查看试题解析
3. 抛物线y＝﹣3（x﹣1）²﹣2的顶点坐标为（）

A、（﹣1，﹣2） B、（1，﹣2） C、（﹣1，2） D、（1，﹣2）

查看试题解析
4. 如图，△ABC中，点D，E分别在AB，AC边上，DE $∥$ BC， $\frac{A D}{B D} = \frac{3}{4}$ ，则 $\frac{A E}{E C}$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{7}$ D、 $\frac{4}{7}$

查看试题解析
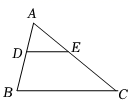5. 用配方法解方程x²+6x+4=0，下列变形正确的是（　　）

A、（x+3）²=﹣4 B、（x﹣3）²=4 C、（x+3）²=5 D、（x+3）²=± $\sqrt{5}$

查看试题解析
6. 若点P（2，﹣3），则点P关于原点的对称点的坐标是（）

A、（2，3） B、（﹣2，﹣3） C、（﹣2，3） D、（2，﹣3）

查看试题解析
7. 把抛物线y＝ $\frac{1}{2}$ x²先向右平移6个单位长度，再向上平移3个单位长度，所得抛物线的函数表达式为（）

A、 $y = \frac{1}{2} {(x + 6)}^{2} + 3$ B、 $y = \frac{1}{2} {(x + 6)}^{2} - 3$ C、 $y = \frac{1}{2} {(x - 6)}^{2} + 3$ D、 $y = \frac{1}{2} {(x - 6)}^{2} - 3$

查看试题解析
8. 如图，△ABC中，点D是AB上一点，补充下列条件后，仍不能判定△ADC∽△ACB的是（）

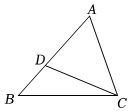A、∠ADC＝∠ACB B、∠ACD＝∠ABC C、 $\frac{A D}{A C}$ ＝ $\frac{A C}{A B}$ D、 $\frac{C D}{B C}$ ＝ $\frac{A C}{A B}$

查看试题解析
9. 足球联赛实行主客场的循环赛，即每两个球队都要在主场和客场各踢一场，某个赛季共举行比赛210场．设共有x个队参赛，可列方程为（）

A、 $\frac{1}{2}$ x（x﹣1）＝210 B、 $\frac{1}{2}$ x（x+1）＝210 C、x（x﹣1）＝210 D、x（x+1）＝210

查看试题解析
10. 关于函数y＝﹣x²﹣2x的图象，有下列说法：①对称轴为直线x＝﹣1；②抛物线开口向上；③从图象可以判断出，当x＞﹣1时，y随着x的增大而减小．其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

11. 关于x的一元二次方程5x²﹣4x+m＝0的一个根是1，则m的值是．

查看试题解析
12. 若关于x的一元二次方程x²﹣4x+m=0有两个不相等的实数根，则m的取值范围为．

查看试题解析
13. 从地面竖直向上抛出一小球，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是 $h = 30 t - 5 t^{2}$ ，则小球从抛出到落地所用的时间是 s.

查看试题解析
14. 《九章算术》是我国古代数学的经典著作，它的出现标志着中国古代数学形成了完整的体系，其“勾股”章中记载了一个数学问题：“今有户高多于广六尺，两隅相去适一丈，问户高、广各几何？”译文为：“已知有一扇矩形门的高比宽多6尺，门的对角线长为1丈（1丈＝10尺），那么门的高和宽各是多少？”如果设门的宽为x尺，则可列方程为．

查看试题解析
15. 如图，在直角坐标系xOy中，点A，点B的坐标分别为（2，﹣1）和（4，2），以O为位似中心，将△AOB缩小为△A′OB′，且△A′OB′与△AOB的相似比为 $\frac{1}{2}$ ，则点B的对应点B′的坐标为．

查看试题解析
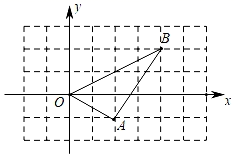16. 如图，矩形ABCD中，AB＝3，BC＝4，点E在边BC上，点F在边CD上，∠AEF＝90°，设BE＝x，CF＝y，当0＜x＜4时，y关于x的函数解析式是．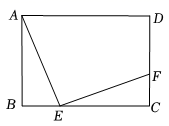

查看试题解析

三、解答题

17. 解方程：

(1)、3x²﹣2x＝0；

(2)、x²+4x﹣10＝0．

查看试题解析
18. 已知二次函数y＝x²+bx+c，画此函数图象时，列表如下：

x

…

0

1

2

3

4

…

y

…

3

0

﹣1

0

3

…

(1)、求出b，c的值；

(2)、当0＜x＜3时，y的取值范围是．

查看试题解析
19. 如图，为了估计河的宽度，我们可以在河对岸选定一个目标点A，在近岸取点B，使AB与河岸垂直，在近岸取点C，E，使BC⊥AB，CE⊥BC，AE与BC交于点D．已测得BD＝40m，DC＝20m，EC＝24m，求河宽AB．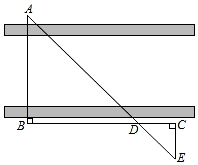

查看试题解析
20. 如图，平面直角坐标系xOy中，点A，点B的坐标分别为（﹣2，1）和（1，2），将线段AB绕点P逆时针方向旋转90°得到线段A′B′，点A的对应点为点A′，点B的对应点为点B′，点A′，B′的坐标分别为（﹣2，﹣1）和（﹣3，2）．

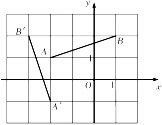(1)、点P的坐标是________（填写选项）；

A、（0，0） B、（1，0） C、（﹣1，0）

(2)、线段BA的延长线与线段A'B′相交于点M，连接AP，BP，A′P，B′P，请补全图形并求出∠BMA′的度数．

查看试题解析
21. 如图，四边形ABCD中，∠BAD＝∠C＝90°，AB＝AD，AE⊥BC，垂足为E，AE＝3，求四边形ABCD的面积．

查看试题解析
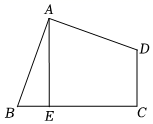22. 如图，利用一面墙（墙的长度为12m），用22m长的篱笆，围成一个矩形场地．

(1)、当BC是多少米时，场地的面积最大？

(2)、若场地的面积为48m² ，求BC的长．

查看试题解析
23. 如图，平面直角坐标系xOy中，抛物线y₁＝﹣ $\frac{\sqrt{2}}{2}$ x²+ $\sqrt{2}$ x+ $\frac{3 \sqrt{2}}{2}$ 的顶点为C，与x轴交于点A，B．抛物线y₂与y₁关于原点对称，y₂的顶点为D，与x轴交于点E，F．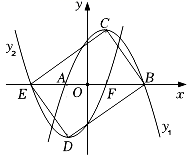

(1)、求y₂的解析式；

(2)、连接BC，CE，DE，BD，判断四边形BCED的形状，并说明理由．

查看试题解析
24. 如图，Rt△ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm，以AC为边向右作正方形ACDE，点P从点C出发，沿射线CD以1cm/s的速度向右运动，过点P作直线l与射线BA交于点Q，使得∠BPQ＝∠B，设运动时间为t（s），△BPQ与正方形ACDE重合部分的面积为S（cm²）．

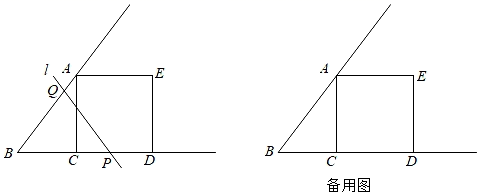(1)、当直线l经过点E时，t的值为．

(2)、求S关于t的函数关系式，并直接写出自变量t的取值范围．

查看试题解析
25. 如图，△ABC中，点D，E在边AB上，点F在边BC上，且AD＝AC，EF＝EC，∠CEF＝∠A，连接DF．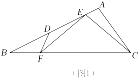

(1)、在图1中找出与∠ACE相等的角，并证明；

(2)、求证：∠BDF＝∠EFC；

(3)、如图2，延长FD，CA交于点G，连接EG，若EG＝AG，DE＝kAE，求 $\frac{D G}{D F}$ 的值（用含k的代数式表示）．

查看试题解析
26. 在平面直角坐标系xOy中，已知抛物线y＝x²﹣（m﹣2）x﹣2m，其中m为常数，点A（﹣2，n）在此抛物线上．

(1)、n的值为；

(2)、若当﹣1≤x≤1时，函数的最大值与最小值的差为3，求m的值．

(3)、抛物线与直线x＝2m+1交于点B，连接AB，过点A作AB的垂线，与y轴交于点C，当AB＝AC时，求m的值．

查看试题解析

x	…	0	1	2	3	4	…
y	…	3	0	﹣1	0	3	…