江西省赣州市经开区2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列汽车标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 将抛物线 $y = 2 x^{2} - 1$ 向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为（）

A、 $y = x {(x - 1)}^{2} + 1$ B、 $y = 2 {(x + 1)}^{2} - 3$ C、 $y = x {(x - 1)}^{2} - 3$ D、 $y = 2 {(x + 1)}^{2} + 1$

查看试题解析
3. 如图，在⊙O中， $\overset{⌢}{A B}$ 所对的圆周角∠ACB＝55°，若P为 $\overset{⌢}{A B}$ 上一点，∠AOP＝73°，OP∥CB ，则∠OBC的度数为（）

A、30° B、35° C、37° D、55°

查看试题解析
4. 如图，一块含30°角的直角三角板ABC绕点C顺时针旋转到△A′B′C，当B，C，A′在一条直线上时，三角板ABC的旋转角度为（）

A、150° B、120° C、60° D、30°

查看试题解析
5. 在平面直角坐标系中，若直线 $y = - x + m$ 不经过第一象限，则关于 $x$ 的方程 $m x^{2} + x + 1 = 0$ 的实数根的个数为（）

A、0个 B、1个 C、2个 D、1或2个

查看试题解析
6. 已知二次函数y＝ax²+bx+c的图像如图所示，下列结论：
①a＞0；②b²﹣4ac＞0；③4a+b＝0；④不等式ax²+（b﹣1）x+c＜0的解集为1＜x＜3．正确的结论个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 若点（a，1）与（﹣2，b）关于原点对称，则a^b= ．

查看试题解析
8. 已知x₁ ， x₂是一元二次方程x²﹣4x+3＝0的两根，则x₁+x₂﹣x₁x₂＝．

查看试题解析
9. 在平面直角坐标系 $x O y$ 中，若抛物线 $y = x^{2} + 2 x + k$ 与x轴只有一个交点，则 $k =$ .

查看试题解析
10. 如图，AB是半圆O的直径，AC为弦，OD⊥AC于D，过点O作OE $∥$ AC交半圆O于点E，过点E作EF⊥AB于F．若AC＝4，则OF的长为．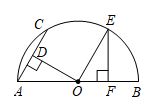

查看试题解析
11. 规定：若 $\vec{a}$ ＝(x₁ ， y₁)， $\vec{b}$ ＝(x₂ ， y₂)，则 $\vec{a} \cdot \vec{b}$ ＝x₁x₂+y₁y₂ ．例如 $\vec{a}$ ＝(1，3)， $\vec{b}$ ＝(2，4)，则 $\vec{a} \cdot \vec{b}$ ＝1×2+3×4＝2+12＝14．已知 $\vec{a}$ ＝(x+1，x﹣1)， $\vec{b}$ ＝(x﹣3，4)，则 $\vec{a} \cdot \vec{b}$ 的最小值是．

查看试题解析
12. 在平面直角坐标系中，正方形ABCD的边AD在y轴正半轴上，边BC在第一象限，且A(0，3)、B(5，3)，将正方形ABCD绕点A顺时针旋转α（0°＜α＜180°），若点B的对应点 $B^{'}$ 恰好落在坐标轴上，则点C的对应点 $C^{'}$ 的坐标为．

查看试题解析

三、解答题

13. 用适当的方法解下列方程：

(1)、x²﹣4x+1＝0；

(2)、3x（x﹣1）＝2﹣2x．

查看试题解析
14. 2021年是中国共产党建党100周年，全国各地积极开展“弘扬红色文化，重走长征路”主题教育学习活动，我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解，今年3月份该基地接待参观人数10万人，5月份接待参观人数增加到12.1万人.

(1)、求这两个月参观人数的月平均增长率；

(2)、按照这个增长率，预计6月份的参观人数是多少？

查看试题解析
15. 如图，已知抛物线L：y＝x²+bx+c经过点A(0，﹣5)，B(5，0)．

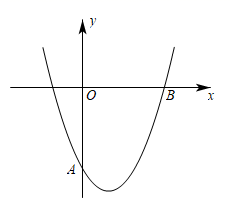(1)、求b，c的值；

(2)、连结AB，交抛物线L的对称轴于点M．求点M的坐标；

查看试题解析
16. 已知：在平面直角坐标系中， $Δ A B C$ 的三个顶点的坐标分别为 $A (5 ， 4)$ ， $B (0 ， 3)$ ， $C (2 ， 1)$ ．

⑴画出 $Δ A B C$ 关于原点成中心对称的 $Δ A_{1} B_{1} C_{1}$ ，并写出点 $C_{1}$ 的坐标；

⑵画出将 $A_{1} B_{1} C_{1}$ 绕点 $C_{1}$ 按顺时针旋转 $90^{\circ}$ 所得的 $Δ A_{2} B_{2} C_{1}$ ．

查看试题解析
17. 如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置.F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H.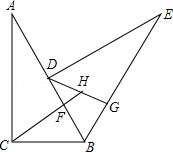

(1)、求证：CF=DG；

(2)、求出∠FHG的度数.

查看试题解析
18. 已知关于x的一元二次方程x²﹣（2k+1）x+2k＝0．

(1)、求证：方程总有两个实数根；

(2)、记该方程的两个实数根为x₁和x₂若以x₁ ， x₂ ， 3为三边长的三角形是直角三角形，求k的值．

查看试题解析
19. 如图，A，B是 $⊙ O$ 上两点，且 $A B = O A$ ，连接OB并延长到点C，使 $B C = O B$ ，连接AC.

(1)、求证：AC是 $⊙ O$ 的切线.

(2)、点D，E分别是AC，OA的中点，DE所在直线交 $⊙ O$ 于点F，G， $O A = 4$ ，求GF的长.

查看试题解析
20. 去年6月，李克强总理提倡搞地摊经济，张明投资销售一种进价为每件20元的护眼台灯，销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y＝﹣10x+500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．

(1)、如果张明想要每月获得的利润为2000元，那么张明每月的单价定为多少元？

(2)、当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？

查看试题解析
21. 我们把方程(x- m)²+(y-n)²=r²称为圆心为(m，n)、半径长为r的圆的标准方程．例如，圆心为(1，-2)、半径长为3的圆的标准方程是(x- 1)²+(y+2)²=9．在平面直角坐标系中，圆C与轴交于点A．B．且点B的坐标为(8.0)，与y轴相切于点D(0， 4)，过点A，B，D的抛物线的顶点为E．

(1)、求圆C的标准方程；

(2)、试判断直线AE与圆C的位置关系，并说明理由．

查看试题解析
22. 如图1，在等腰直角三角形ABC中，∠BAC＝90°，点E，F分别为AB，AC的中点，H为线段EF上一动点（不与点E，F重合），将线段AH绕点A逆时针方旋转90°，得到AG，连接GC，HB．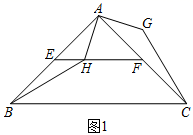

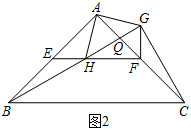(1)、证明： $△$ AHB≌ $△$ AGC

(2)、如图2，连接HG和GF，其中HG交AF于点Q．
①证明：在点H的运动过程中，总有∠HFG＝90°；

②若AB＝AC＝4，当EH的长度为多少时， $△$ AQG为等腰三角形？

查看试题解析
23. 抛物线C₁：y₁＝x²﹣1﹣2t（x﹣1）（t≠1）与x轴交于A，B两点（点A在点B的左侧）．

(1)、①填空：当t＝﹣2时，点A的坐标为 ▲ ，点B的坐标为 ▲ ；当t＝0时，点A的坐标为 ▲ ，点B的坐标为 ▲ ；
②随t值的变化，抛物线C₁是否会经过某一个定点，若会，请求出该定点的坐标；若不会，请说明理由；

(2)、若将抛物线C₁经过适当平移后，得到抛物线C₂：y₂＝（x﹣t）²+t﹣1，A，B的对应点分别为D（m，n），E（m+2，n），求抛物线C₂的解析式；

(3)、设抛物线C₁的顶点为P，当t＞0，△APB为直角三角形时，求方程x²﹣1﹣2t（x﹣1）＝0（t≠1）的根．

查看试题解析