黑龙江省讷河市十所2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
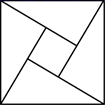 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 和平中学为了排污,需铺设一段全长为7200米的排污管道,为减少施工对居民生活的影响,须缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前4天完成任务,设原计划每天铺设 米,下面所列方程正确的是( )A、 B、 C、 D、4. 若关于x的不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、5. 一张桌子上摆着若干个碟子,从三个方向上看所得的视图如图所示,则这张桌子上碟子的数量为( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 和平中学为了排污,需铺设一段全长为7200米的排污管道,为减少施工对居民生活的影响,须缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前4天完成任务,设原计划每天铺设 米,下面所列方程正确的是( )A、 B、 C、 D、4. 若关于x的不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、5. 一张桌子上摆着若干个碟子,从三个方向上看所得的视图如图所示,则这张桌子上碟子的数量为( ) A、17 B、13 C、12 D、96. 下列语句中,表示不可能事件的是( )A、绳锯木断 B、杀鸡取卵 C、钻木取火 D、水中捞月7. 如图, 中, , , 的平分线 交 于点F, 平分 .给出下列结论:① ;② ;③ ;④ .符合题意结论有( )
A、17 B、13 C、12 D、96. 下列语句中,表示不可能事件的是( )A、绳锯木断 B、杀鸡取卵 C、钻木取火 D、水中捞月7. 如图, 中, , , 的平分线 交 于点F, 平分 .给出下列结论:① ;② ;③ ;④ .符合题意结论有( )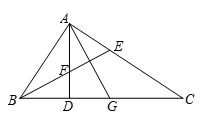 A、1个 B、2个 C、3个 D、4个8. 今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )A、2种 B、3种 C、4种 D、5种9. 如图, 中, , , ,P是对角线AC上任一点(点P不与点A、C重合),且 交AB于E,且 交AD于F,则阴影部分的面积为( )
A、1个 B、2个 C、3个 D、4个8. 今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )A、2种 B、3种 C、4种 D、5种9. 如图, 中, , , ,P是对角线AC上任一点(点P不与点A、C重合),且 交AB于E,且 交AD于F,则阴影部分的面积为( )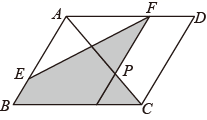 A、5 B、 C、10 D、10. 如图,二次函数 的图象与 轴交于 , 两点,与 轴正半轴交于点 ,它的对称轴为直线 .则下列选项中① ;② ;③ ;④ :⑤当 ( 为实数)时, ,其中正确的有( )
A、5 B、 C、10 D、10. 如图,二次函数 的图象与 轴交于 , 两点,与 轴正半轴交于点 ,它的对称轴为直线 .则下列选项中① ;② ;③ ;④ :⑤当 ( 为实数)时, ,其中正确的有( )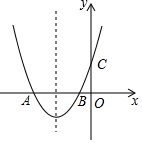 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. “我的连云港” 是全市统一的城市综合移动应用服务端.一年来,实名注册用户超过1600000人.数据“1600000”用科学记数法表示为.12. 若关于x的分式方程 的解为正数,则a的取值范围为 .13. 已知一组数据-3,-2,1,3,6,x的中位数为1,则其方差为 .14. 若关于x的函数 的图象与x轴仅有一个交点,则实数k的值为 .15. 等腰 一腰上的高与另一腰的夹角为50°,则 顶角的度数为 .16. 关于x的函数 (a为实数)的函数上两点 、 ,则 (填>、<、=号)17. 在平面直角坐标系中,点 在 轴的正半轴上, , , , , , .按此规律,则 的长为 .

三、解答题
-
18.(1)、计算: ;(2)、分解因式: .19. 解方程: .20. 如图,在 中,∠B=∠C,点D在BC边上,点E在AC边上,且∠ADE=∠ AED,连接DE.
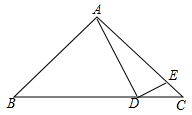 (1)、若∠BAD=50°,DA=DB,求∠CDE的度数.(2)、猜想∠CDE与∠BAD的数量关系,并说明理由.21. 随着疫情的发展,“勤洗手,戴口罩”六字已深入人心,小华就某城区公众对在公共场合制止不戴口罩的态度进行了随机抽样调查,主要有四种态度:A.赞成保安对不戴口罩的出面制止:B.赞成群众对不戴口罩的出面制止:C.赞成防疫人员对不戴口罩的出面制止;D.无所谓,他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
(1)、若∠BAD=50°,DA=DB,求∠CDE的度数.(2)、猜想∠CDE与∠BAD的数量关系,并说明理由.21. 随着疫情的发展,“勤洗手,戴口罩”六字已深入人心,小华就某城区公众对在公共场合制止不戴口罩的态度进行了随机抽样调查,主要有四种态度:A.赞成保安对不戴口罩的出面制止:B.赞成群众对不戴口罩的出面制止:C.赞成防疫人员对不戴口罩的出面制止;D.无所谓,他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题: (1)、求这次抽样的公众有多少人?(2)、请将统计图①补充完整;(3)、在统计图②中,求“无所谓”部分所对应的圆心角是多少度?(4)、若该城区人口有20万人,估计赞成“防疫人员对不戴口罩的出面制止”的有多少万人?(5)、小华在该城区随机对路人进行调查,请你根据以上信息,直接写出赞成“防疫人员对不戴口罩的出面制止”的概率是 .22. 一队学生从学校出发去劳动基地,行进的路程与时间的函数图象如图所示,队伍走了0.8小时后,队伍中的通讯员按原路加快速度返回学校取材料.通讯员经过一段时间回到学校,取到材料后立即按返校时加快的速度追赶队伍,并比学生队伍早18分钟到达基地.如图,线段OD表示学生队伍距学校的路程y(千米)与时间x(小时)之间的函数关系,折线OABC表示通讯员距学校的路程y(千米)与时间x(小时)之间的函数关系,请你根据图象信息,解答下列问题:
(1)、求这次抽样的公众有多少人?(2)、请将统计图①补充完整;(3)、在统计图②中,求“无所谓”部分所对应的圆心角是多少度?(4)、若该城区人口有20万人,估计赞成“防疫人员对不戴口罩的出面制止”的有多少万人?(5)、小华在该城区随机对路人进行调查,请你根据以上信息,直接写出赞成“防疫人员对不戴口罩的出面制止”的概率是 .22. 一队学生从学校出发去劳动基地,行进的路程与时间的函数图象如图所示,队伍走了0.8小时后,队伍中的通讯员按原路加快速度返回学校取材料.通讯员经过一段时间回到学校,取到材料后立即按返校时加快的速度追赶队伍,并比学生队伍早18分钟到达基地.如图,线段OD表示学生队伍距学校的路程y(千米)与时间x(小时)之间的函数关系,折线OABC表示通讯员距学校的路程y(千米)与时间x(小时)之间的函数关系,请你根据图象信息,解答下列问题: (1)、图中的 千米, 小时,点B的坐标为;(2)、求通讯员距学校的路程y(千米)与时间x(小时)之间的函数关系式;(3)、若通讯员与学生队伍的距离不超过3千米时能用无线对讲机保持联系,请你直接写出通讯员离开队伍后他们能用对讲机保持联系的时间的取值范围.
(1)、图中的 千米, 小时,点B的坐标为;(2)、求通讯员距学校的路程y(千米)与时间x(小时)之间的函数关系式;(3)、若通讯员与学生队伍的距离不超过3千米时能用无线对讲机保持联系,请你直接写出通讯员离开队伍后他们能用对讲机保持联系的时间的取值范围.答: .
23. 如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能合成一个无缝隙,无重叠的矩形,这样的矩形称为叠合矩形. (1)、将▱ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 , ;S矩形AEFG:S▱ABCD= .(2)、如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出叠合正方形的示意图,并求出AD、BC的长.24. 综合与探究
(1)、将▱ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 , ;S矩形AEFG:S▱ABCD= .(2)、如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出叠合正方形的示意图,并求出AD、BC的长.24. 综合与探究如图1所示,直线y=x+c与x轴交于点A(-4,0),与y轴交于点C,抛物线y=-x2+bx+c经过点A,C.
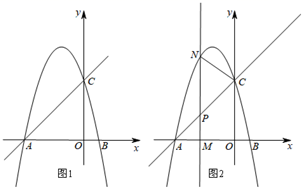 (1)、求抛物线的解析式;(2)、点E在抛物线的对称轴上,求CE+OE的最小值为 .(3)、如图2所示,M是线段OA的上一个动点,过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N
(1)、求抛物线的解析式;(2)、点E在抛物线的对称轴上,求CE+OE的最小值为 .(3)、如图2所示,M是线段OA的上一个动点,过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N①当 面积最大时的P点坐标为 ▲ ;最大面积为 ▲ .
②点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D、F、B、C为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.