广东省汕头市潮阳区十校联考2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的是（　　）

A、x²+2xy＝1 B、x²+x+1 C、x²＝4 D、ax²+bx+c＝0

查看试题解析
2. 一元二次方程x²﹣x+2=0的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、只有一个实数根

查看试题解析
3. 抛物线 $y = {(x - 2)}^{2} + 2$ 的顶点坐标是（）．

A、 $(- 2 ， 2)$ B、 $(2 ， - 2)$ C、 $(2 ， 2)$ D、 $(- 2 ， - 2)$

查看试题解析
4. 下列图形中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 一元二次方程x²﹣6x﹣5=0配方可变形为（）

A、（x﹣3）²=14 B、（x﹣3）²=4 C、（x+3）²=14 D、（x+3）²=4

查看试题解析
6. 若x支球队参加篮球比赛，共比赛了36场，每2队之间比赛一场，则下列方程中正确的是 $($ $)$

A、 $x (x - 1) = 36$ B、 $x (x + 1) = 36$ C、 $\frac{1}{2} x (x - 1) = 36$ D、 $\frac{1}{2} x (x + 1) = 36$

查看试题解析
7. 如图，在Rt△ABC中，∠BAC＝90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C，点A在边B′C上，则∠B′的大小为（）

A、42° B、48° C、52° D、58°

查看试题解析
8. 如图，△ABC的三个顶点都在方格纸的格点上，其中点A的坐标是（﹣1，0）．现将△ABC绕点A顺时针旋转90°，则旋转后点C的坐标是（）

A、（2，1） B、（1，2） C、（-2，-1） D、（-2，1）

查看试题解析
9. 点P₁(﹣2，y₁)，P₂(2，y₂)，P₃(4，y₃)均在二次函数y＝﹣x²+2x+c的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₂＞y₃＞y₁ B、y₂＞y₁＝y₃ C、y₁＝y₃＞y₂ D、y₁＝y₂＞y₃

查看试题解析
10. 如图，正方形ABCD的边长为2m，点P，点Q同时从点A出发，速度均2cm/s，点P沿A-D-C向点C运动，点Q沿A-B-C向点C运动，则△APQ的面积S（cm²）与运动时间t（s）之间函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若 $M (3, y)$ 与 $N (x, y - 1)$ 关于原点对称，则 $x y$ 的值为.

查看试题解析
12. 若关于 $x$ 的一元二次方程 $k x^{2} - x + 1 = 0$ 有实数根，则 $k$ 的取值范围是．

查看试题解析
13. 如图，将等边 $△ A B C$ 绕顶点A顺时针方向旋转，使边AB与AC重合得 $△ A C D$ ， $B C$ 的中点E的对应点为F，则 $∠ E A F$ 的度数是．

查看试题解析
14. 将抛物线 $y = - 2 {(x - 1)}^{2}$ 向左平移2个单位再向上平移3个单位所得到的抛物线解析式是．

查看试题解析
15. 若一元二次方程 $a x^{2} - b x - 2020 = 0$ 有一根为 $x = - 1$ ，则 $a + b =$ .

查看试题解析
16. 若点 $(- 3 ， 5)$ 、 $(5 ， 5)$ 在抛物线 $y = a x^{2} + b x + 1$ 上，则该抛物线的对称轴是

查看试题解析
17. 如图，边长为1的正方形ABCD，将正方形ABCD绕顶点A顺时针旋转45°得到正方形AB′C′D′，则图中阴影部分的面积为．

查看试题解析

三、解答题

18. 解方程： $\frac{1}{2} {(x - 3)}^{2} = 2 x - 6$ ．

查看试题解析
19. 已知抛物线 $y = x^{2} - 2 x - 3$ ．

(1)、求抛物线与两坐标轴的交点坐标；

(2)、求它的顶点坐标，

查看试题解析
20. 2018年，某市某楼准备以每平方米5000元的均价对外销售，因为楼盘滞销，房地产开发商为了加快资金的周转，决定进行降价促销，经过连续两年的下调后，2020年的均价为每平方米4050元．求平均每年下调的百分率．

查看试题解析
21. 如图，等腰Rt△ABC中，BA=BC，∠ABC=90°，点D在AC上，将△ABD绕点B沿顺时针方向旋转90°后，得到△CBE．

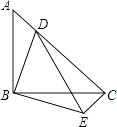(1)、求∠DCE的度数；

(2)、若AB=4，CD=3AD，求DE的长．

查看试题解析
22. 已知关于 $x$ 的一元二次方程x²-(k+2)x+k-1=0

(1)、若方程的一个根为 -1，求 $k$ 的值和方程的另一个根；

(2)、求证：不论 $k$ 取何值，该方程都有两个不相等的实数根．

查看试题解析
23. 欧尚超市准备代销一款运动鞋，每双的成本是160元，为了合理定价，投放市场进行试销．据市场调查，销售单价是200元时，每天的销售量是40双，而销售单价每降低1元，每天就可多售出6双（售价不得低于160元/双），设每双降低售价x元（x为正整数），每天的销售利润为y元．

(1)、求y与x的函数关系式，并直接写出自变量x的取值范围；

(2)、每双运动鞋的售价定为多少元时，每天可获得最大利润？最大利润是多少？

查看试题解析
24. 如图①，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC

(1)、试探索线段BC，DC，EC之间满足的等量关系，并证明你的结论．

(2)、如图②，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论．

查看试题解析
25. 如图，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 与x轴交于 $A ， B$ 两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知 $A (- 1 ， 0) ， C (0 ， 2)$ ．

(1)、求抛物线的解析式；

(2)、在抛物线的对称轴上是否存在点P，使 $△ P C D$ 是以 $C D$ 为腰的等腰三角形？如果存在，直接写出点P的坐标；如果不存在，请说明理由；

(3)、点E是线段 $B C$ 上的一个动点，过点E作x轴的垂线与抛物线相交于点F，求 $△ C B F$ 的最大面积及此时点E的坐标．

查看试题解析