广东省广州市白云区永平片2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 若关于x的方程（m﹣1）x²+mx﹣1＝0是一元二次方程，则m的取值范围是（）

A、m≠1 B、m＝1 C、m≥1 D、m≠0

查看试题解析
2. 抛物线y=3（x﹣1）²+2的顶点坐标是（）

A、（1，﹣2） B、（﹣1，2） C、（1，2） D、（﹣1，﹣2）

查看试题解析
3. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 已知抛物线y＝ax²+bx+c与x轴的两个交点坐标是（﹣2，0），（5，0），则一元二次方程ax²+bx+c＝0的两个解是（）

A、x₁＝﹣2，x₂＝5 B、x₁＝2，x₂＝﹣5 C、x₁＝﹣2，x₂＝﹣5 D、x₁＝2，x₂＝5

查看试题解析
5. 已知关于x的一元二次方程x²﹣2x﹣k＝0有两个不相等的实数根，则实数k的取值范围是（　　）

A、k≥1 B、k＞1 C、k≥﹣1 D、k＞﹣1

查看试题解析
6. 将二次函数y=x²的图象向右平移1个单位，再向上平移2个单位后，所得图象的函数表达式是（　　）

A、y=（x-1）²+2 B、y=（x+1）²+2 C、y=（x-1）²-2 D、y=（x+1）²-2

查看试题解析
7. 用配方法解方程x²﹣4x﹣7＝0，可变形为（）

A、（x+2）²＝3 B、（x+2）²＝11 C、（x﹣2）²＝3 D、（x﹣2）²＝11

查看试题解析
8. 在某次聚会上，每两人都握了一次手，所有人共握手15次，设有x人参加这次聚会，则列出方程正确的是（）

A、x（x﹣1）=15 B、 $\frac{x (x - 1)}{2}$ =15 C、x（x+1）=15 D、 $\frac{x (x + 1)}{2}$ =15

查看试题解析
9. 关于x的方程（x+1）²﹣3（x+1）＝2的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个不相等的实数根 D、有两个相等的实数根

查看试题解析
10. 如图，已知△ABC 中，∠C＝90°，AC＝BC＝ $\sqrt{2}$ ，将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置，连接 C′B，则 C′B 的长为（）

A、2－ $\sqrt{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\sqrt{3} - 1$ D、1

查看试题解析

二、填空题

11. 若点（m，3）与点（2，n）关于原点对称，则m+n＝．

查看试题解析
12. 关于x的一元二次方程x²＋x﹣a＝0的一个是2，则a＝．

查看试题解析
13. 某商场一月份利润为100万元，三月份的利润为121万元，则该商场二、三月利润的平均增长率为x，则可列出方程为．

查看试题解析
14. 发射一枚炮弹，经 $x$ 秒后的高度为 $y$ 米，且时间与高度的关系为 $y = a x^{2} + b x + c (a \neq 0)$ ．若此炮弹在第7秒与第15秒时的高度相等，则第秒时炮弹位置达到最高．

查看试题解析
15. 在直角坐标平面内，有点A（﹣2，0），B（0，2），将线段AB绕点B顺时针旋转后，点A的对应点C落在y轴上，那么旋转角是 °．

查看试题解析
16. 如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ABE绕点A顺时针旋转90°后，得到△ACF，连接DF，下列结论中：①∠DAF＝45°②△ABE≌△ACD③AD平分∠EDF④BE²+DC²＝DE²；正确的有（填序号）

查看试题解析

三、解答题

17. 解方程： $x^{2} + 4 x = 0$ .

查看试题解析
18. 已知：关于x的一元二次方程x²+kx﹣1=0，求证：方程有两个不相等的实数根．

查看试题解析
19. 如图，已知抛物线 $y = x^{2} + b x + c$ 经过点A（-1，0）、C（0，-3）两点．

(1)、求抛物线解析式和顶点坐标；

(2)、当0＜x＜3时，请直接写出y的取值范围．

查看试题解析
20. 如图，△ABC的顶点坐标分别为A（0，1），B（3，3），C（1，3）．

⑴画出△ABC关于原点O成中心对称的△A₁B₁C₁；

⑵画出△ABC关于x轴对称的△A₂B₂C₂ ．

查看试题解析
21. 学校计划利用一片空地建一个花圃，花圃为矩形，其中一面靠墙（墙足够长），另三面用总长28米的篱笆材料围成，且计划建造花圃的面积为80平方米．那么这个花圃的长和宽分别应为多少米？

查看试题解析
22. 如图，已知二次函数y＝﹣x²+2x+3图象与x轴的其中一个交点为A，与y轴交于点B，若直线AB与这个二次函数图象的对称轴交于点P，求点P的坐标．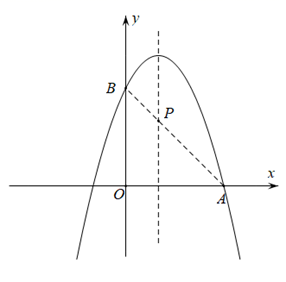

查看试题解析
23. 如图，△ABC中，AB＝AC＝2，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D．

(1)、求证：BE＝CF；

(2)、当四边形ACDE为菱形时，求BD的长．

查看试题解析
24. 如图1，抛物线y＝ax²+bx+c与x轴交于A、B（3，0）两点（A在B的左侧），与y轴交于点C（0，3），已知对称轴为x＝1．

(1)、求抛物线L的解析式；

(2)、如图2，设点P是抛物线L在x轴上方任一点，点Q在直线x＝﹣3上，△PBQ能否成为以P为直角顶点的等腰直角三角形？若能，求出符合条件的点P的坐标；若不能，请说明理由．

查看试题解析
25. 阅读下面材料，并解决问题：

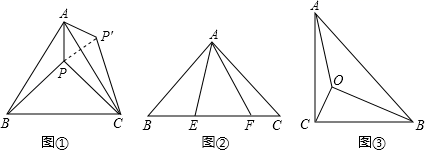(1)、如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．
为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB＝；

(2)、基本运用
请你利用第（1）题的解答思想方法，解答下面问题：

已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF²＝BE²+FC²；

(3)、能力提升
如图③，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC＝∠COB＝∠BOA＝120°，求OA+OB+OC的值．

查看试题解析