安徽省宿州市埇桥区教育集团2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中是关于x的一元二次方程的是（）

A、x²＋ $\frac{1}{x}$ ＝0 B、(x－1)²＝(x＋3)(x－2)＋1 C、x＝x² D、ax²＋bx＋c＝0

查看试题解析
2. 四条线段 $a, b, c, d$ 成比例,其中 $a$ ＝3 $c m$ ， $d = 4 c m$ ， $c = 6 c m$ ，则 $b$ 等于（）

A、2㎝ B、 $\frac{2}{9}$ ㎝ C、 $\frac{9}{2} c m$ D、8㎝

查看试题解析
3. 若△ABC∽△DEF，△ABC与△DEF的面积之比为4：25，则△ABC与△DEF周长之比为（）

A、4：25 B、2：5 C、5：2 D、25：4

查看试题解析
4. 如图，菱形ABCD中，AC交BD于点O，DE⊥BC于点E，连接OE，若∠BCD＝50°，则∠OED的度数是（）

A、35° B、30° C、25° D、20°

查看试题解析
5. 在一个不透明的布袋中装有40个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.30左右，则布袋中黄球可能有（）

A、12个 B、14个 C、18个 D、28个

查看试题解析
6. 下列方程中有两个相等实数根的是（）

A、x²+1＝2x B、x²+1＝0 C、x²﹣2x﹣3=0 D、x²﹣2x＝0

查看试题解析
7. 某种药品原价为36元/盒，经过连续两次降价后售价为25元/盒．设平均每次降价的百分率为x，根据题意所列方程正确的是（）

A、36（1﹣x）²=36﹣25 B、36（1﹣2x）=25 C、36（1﹣x）²=25 D、36（1﹣x²）=25

查看试题解析
8. 如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 $\frac{1}{3}$ ，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点坐标为（）

A、（3，2） B、（3，1） C、（2，2） D、（4，2）

查看试题解析
9. 宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ （约0.618）的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，给我们以协调和匀称的美感．我们可以用这样的方法画出黄金矩形：作正方形ABCD，分别取AD、BC的中点E、F，连接EF：以点F为圆心，以FD为半径画弧，交BC的延长线于点G；作GH⊥AD，交AD的延长线于点H，则图中下列矩形是黄金矩形的是（　　）

A、矩形ABFE B、矩形EFCD C、矩形EFGH D、矩形DCGH

查看试题解析
10. 如图，在矩形ABCD中，AB＝3，AD＝4，以BC为斜边在矩形的外部作直角三角形BEC，点F是CD的中点，则EF的最大值为（）

A、 $\frac{\sqrt{73}}{2}$ B、4 C、5 D、 $\frac{9}{2}$

查看试题解析

二、填空题

11. 若 $\frac{y}{x}$ ＝3，则 $\frac{x + y}{x}$ 的值为

查看试题解析
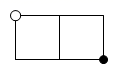
12. 若实数x，y满足（x²+y²+1）（x²+y²﹣2）＝0，则x²+y²的值是．

查看试题解析
13. 如图，小颖在围棋盘上两个格子的格点上任意摆放黑、白两个棋子，且两个棋子不在同一条网格线上，其中，恰好摆放成如图所示位置的概率是．

查看试题解析
14. 图（1）是一张矩形纸片，将其依次按图（2）、图（3）的方式折叠，AE与AD恰好重合．

(1)、如图（3），折痕AM与EF交于点G，则∠AGD＝．

(2)、若 $△$ DFG的面积为S，则矩形ABCD的面积为．

查看试题解析

三、解答题

15. 解方程：

(1)、x²+3x+2＝0；

(2)、2（x+3）²＝x（x+3）．

查看试题解析
16. △ABC中，a，b，c分别为它的三边，且a＋b＋c＝60，a∶b∶c＝3∶4∶5，求△ABC的面积．

查看试题解析
17. 如图，△ABC三个顶点坐标分别为A(1，2）、B(3，1）、C(2，3)，以原点O为位似中心，将△ABC放大为原来的2倍得 $△ A^{'} B^{'} C^{'}$ ．

(1)、在图中第一象限内画出符合要求的 $△ A^{'} B^{'} C^{'}$ (不要求写画法)；

(2)、 $△ A^{'} B^{'} C^{'}$ 的面积是：.

查看试题解析

18. 如表，方程1、方程2、方程3…是按照一定的规律排列的一列方程，

(1)、解方程3，并将它的解填在表中的空白处．

序号	方程	方程的解
1	x²+2x﹣3＝0	x₁＝1	x₂＝﹣3
2	x²+4x﹣12＝0	x₁＝2	x₂＝﹣6
3	x²+6x﹣27＝0	x₁＝	x₂＝
…	…	…	…

(2)、请写出这列方程中第m个方程，并写出它的解；

(3)、用你探究的规律求方程x²+20x﹣300＝0的解．

查看试题解析

19. 为了解某校落实新课改精神的情况，现以该校某班的同学参加课外活动的情况为样本，对其参加“球类”，“绘画类”，“舞蹈类”，“音乐类”，“棋类”活动的情况进行调查统计，并绘制了如图所示的统计图．

(1)、参加音乐类活动的学生人数为人，参加球类活动的人数的百分比为；

(2)、请把条形统计图补充完整；

(3)、若该校学生共1600人，那么参棋类活动的大约有多少人？

(4)、该班参加舞蹈类活动4位同学中，有1位男生（用 $E$ 表示）和3位女生（分别 $F$ ， $G$ ， $H$ 表示），现准备从中选取两名同学组成舞伴，请用列表或画树状的方法求恰好选中一男一女的概率．

查看试题解析
20. 如图，在△ABC中，D、E分别是AC、AB的中点，CF∥AB交ED的延长线于点F，连接AF、CE.

(1)、求证：四边形BCEF是平行四边形；

(2)、当△ABC满足什么条件时，四边形AECF是菱形.

查看试题解析
21. 某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓是单价为40元，设第二个月单价降低 $x$ 元．

(1)、填表：（不需化简）

时间

第一个月

第二个月

清仓时

单价（元）

80

40

销售量（件）

200

(2)、如果批发商希望通过销售这批T恤获利9000元，那么第二个月的单价应是多少元？

查看试题解析
22. 如图，在 $△$ ABC中，D，E分别是AB，AC上的点，DC交BE于点F，且AD＝ $\frac{1}{3}$ AB，AE＝ $\frac{1}{2}$ EC．

(1)、求证： $△$ DEF∽ $△$ CBF；

(2)、DF•BF＝EF•CF．

查看试题解析
23. 如图1所示，在等边三角形ABC中，线段AD为其内角平分线，过点D的直线B₁C₁⊥AC于点C₁ ，交AB的延长线于点B₁ ．

(1)、请你探究： $\frac{A C}{A B} = \frac{C D}{B D} ， \frac{A C_{1}}{A B_{1}} = \frac{D C_{1}}{D B_{1}}$ 是否都成立？请说明理由．

(2)、请你继续探究：若 $△$ ABC为任意三角形，线段AD为其内角平分线， $\frac{A C}{A B} = \frac{C D}{D B}$ 一定成立吗？并证明你的判断．

(3)、如图2所示，在Rt $△$ ABC中，∠ACB＝90°，AC＝8，AB＝ $\frac{40}{3}$ ，E为AB上一点且AE＝5，CE交内角平分线AD于点F，试求 $\frac{D F}{F A}$ 的值．

查看试题解析

时间	第一个月	第二个月	清仓时
单价（元）	80		40
销售量（件）	200