初数浙教版九上相似三角形的判定及应用 专项复习(困难版)
试卷更新日期:2021-12-22 类型:复习试卷
一、单选题
-
1. 已知△ABC中,∠BAC=90°,用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形,其作法错误的是( )A、
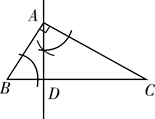 B、
B、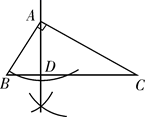 C、
C、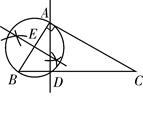 D、
D、 2. 如果两个相似三角形的对应边之比为2:5,其中一个三角形的一个内角的角平分线长为7,则另一个三角形对应角平分线的长为( )A、 B、 C、 或 D、无法确定3. 如图,小颖把一面镜子水平放置在离树底(点B)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢(点A),已知 米,小颖目高 米,则树的高度AB为( )
2. 如果两个相似三角形的对应边之比为2:5,其中一个三角形的一个内角的角平分线长为7,则另一个三角形对应角平分线的长为( )A、 B、 C、 或 D、无法确定3. 如图,小颖把一面镜子水平放置在离树底(点B)8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢(点A),已知 米,小颖目高 米,则树的高度AB为( )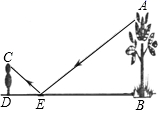 A、3.2米 B、4.8米 C、8米 D、20米4. 如图,小正方形的边长均为 ,则 、 、 、 四个选项中的三角形(阴影部分)与 相似的是( )
A、3.2米 B、4.8米 C、8米 D、20米4. 如图,小正方形的边长均为 ,则 、 、 、 四个选项中的三角形(阴影部分)与 相似的是( )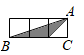 A、
A、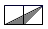 B、
B、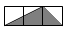 C、
C、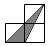 D、
D、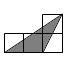 5. 根据下列各组条件,不能判定△ABC∽△A1B1C1的是( )A、∠B=∠B1=60°,∠C=50°,∠A1=70° B、∠C=∠C1=90°,AB=10,AC=6,A1B1=5,A1C1=3 C、∠A=40°,AB=2,AC=3,∠A1=40°,A1B1=4,A1C1=5 D、AB=12,BC=15,AC=24,A1B1=8,A1C1=16,B1C1=106. 如图,在 中, , ,以点 为圆心,以 的长为半径作弧交 于点 ,连接 ,再分别以点 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,连接 ,则下列结论中错误的是 ( )
5. 根据下列各组条件,不能判定△ABC∽△A1B1C1的是( )A、∠B=∠B1=60°,∠C=50°,∠A1=70° B、∠C=∠C1=90°,AB=10,AC=6,A1B1=5,A1C1=3 C、∠A=40°,AB=2,AC=3,∠A1=40°,A1B1=4,A1C1=5 D、AB=12,BC=15,AC=24,A1B1=8,A1C1=16,B1C1=106. 如图,在 中, , ,以点 为圆心,以 的长为半径作弧交 于点 ,连接 ,再分别以点 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,连接 ,则下列结论中错误的是 ( )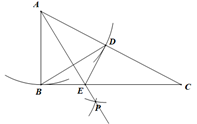 A、 B、 垂直平分线段 C、 D、7. 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )
A、 B、 垂直平分线段 C、 D、7. 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )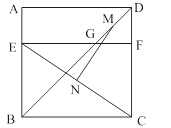 A、3 B、 C、 D、48. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
A、3 B、 C、 D、48. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,
其中正确的结论的个数是( )
 A、1 B、2 C、3 D、49.
A、1 B、2 C、3 D、49.如图,已知在 中, , , ,点 是 的重心,则点 到 所在直线的距离等于( )
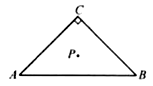 A、 B、 C、 D、10. 如图,在
A、 B、 C、 D、10. 如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG= , 则ΔCEF的周长等于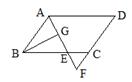 A、8 B、9.5 C、10 D、11.5
A、8 B、9.5 C、10 D、11.5二、填空题
-
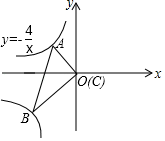
11. 如图,将一个含30°角的三角尺ABC放在直角坐标系中,使直角顶点C与原点O重合,顶点A,B分别在反比例函数y=﹣ 和y= 的图象上,则k的值为.
 12. 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.
12. 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.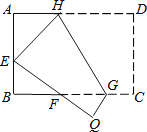 13. 三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则△ABE的周长为cm.
13. 三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则△ABE的周长为cm.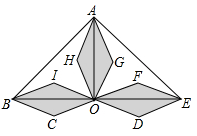 14. 如图,直线l1∥l2∥l3 , A,B,C分别为直线l1 , l2 , l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1 , l2之间的距离为m,直线l2 , l3之间的距离为n,若∠ABC=90°,BD=4,且 则m+n的最大值为.
14. 如图,直线l1∥l2∥l3 , A,B,C分别为直线l1 , l2 , l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1 , l2之间的距离为m,直线l2 , l3之间的距离为n,若∠ABC=90°,BD=4,且 则m+n的最大值为.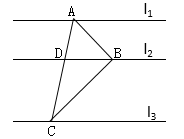 15. 如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的OP与△ABC的一边相切时,AP的长为.
15. 如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的OP与△ABC的一边相切时,AP的长为.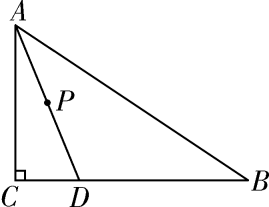 16. 如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=EH,那么EH的长为 .
16. 如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=EH,那么EH的长为 .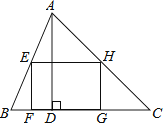
三、综合题
-
17. 如图,在矩形 中, , ,点 是 的中点.
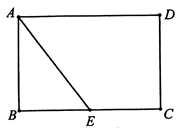 (1)、尺规作图:在 上求作一点 ,使 ;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求 的长.18. 已知AB为⊙O的直径,BC⊥AB于B,且BC=AB,D为半圆⊙O上的一点,连接BD并延长交半圆⊙O的切线AE于E.(1)、如图1,若CD=CB,求证:CD是⊙O的切线;
(1)、尺规作图:在 上求作一点 ,使 ;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求 的长.18. 已知AB为⊙O的直径,BC⊥AB于B,且BC=AB,D为半圆⊙O上的一点,连接BD并延长交半圆⊙O的切线AE于E.(1)、如图1,若CD=CB,求证:CD是⊙O的切线; (2)、如图2,若F点在OB上,且CD⊥DF,求 的值.
(2)、如图2,若F点在OB上,且CD⊥DF,求 的值.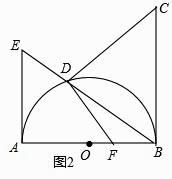 19. 如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
19. 如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.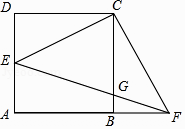 (1)、求证:△CDE≌△CBF;(2)、当DE= 时,求CG的长;(3)、连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.20. 如图1,抛物线 平移后过点A(8,0)和原点,顶点为B,对称轴与 轴相交于点C,与原抛物线相交于点D.
(1)、求证:△CDE≌△CBF;(2)、当DE= 时,求CG的长;(3)、连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.20. 如图1,抛物线 平移后过点A(8,0)和原点,顶点为B,对称轴与 轴相交于点C,与原抛物线相交于点D.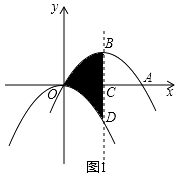
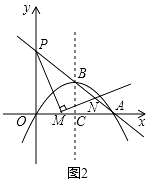
 (1)、求平移后抛物线的解析式并直接写出阴影部分的面积 ;(2)、如图2,直线AB与 轴相交于点P,点M为线段OA上一动点, 为直角,边MN与AP相交于点N,设 ,试探求:
(1)、求平移后抛物线的解析式并直接写出阴影部分的面积 ;(2)、如图2,直线AB与 轴相交于点P,点M为线段OA上一动点, 为直角,边MN与AP相交于点N,设 ,试探求:① 为何值时 为等腰三角形;
②
 为何值时线段PN的长度最小,最小长度是多少.
为何值时线段PN的长度最小,最小长度是多少.