初数浙教版九上相似三角形的判定及应用 专项复习(普通版)
试卷更新日期:2021-12-22 类型:复习试卷
一、单选题
-
1. 如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )
 A、5 B、6 C、7 D、82. 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )
A、5 B、6 C、7 D、82. 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )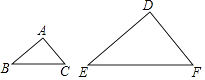 A、 = B、 = C、 = D、 =3. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A、 = B、 = C、 = D、 =3. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )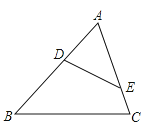 A、∠AED=∠B B、∠ADE=∠C C、= D、=4. 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
A、∠AED=∠B B、∠ADE=∠C C、= D、=4. 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( ) A、10m B、12m C、12.4m D、12.32m5. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y= (x>0)的图象上,则经过点B的反比例函数解析式为( )
A、10m B、12m C、12.4m D、12.32m5. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y= (x>0)的图象上,则经过点B的反比例函数解析式为( )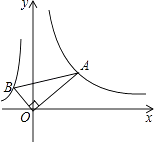 A、y=﹣ B、y=﹣ C、y=﹣ D、y=6. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
A、y=﹣ B、y=﹣ C、y=﹣ D、y=6. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( ) A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形7. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形7. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )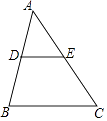 A、6 B、12 C、18 D、248. 如图,小明在A时测得某树的影长为4米,B时又测得该树的影长为1米,若两次日照的光线互相垂直,则树的高度为( )米.
A、6 B、12 C、18 D、248. 如图,小明在A时测得某树的影长为4米,B时又测得该树的影长为1米,若两次日照的光线互相垂直,则树的高度为( )米. A、2 B、4 C、6 D、89. 如图,在正方形网格上,与△ABC相似的三角形是( )
A、2 B、4 C、6 D、89. 如图,在正方形网格上,与△ABC相似的三角形是( ) A、△AFD B、△FED C、△AED D、不能确定10. 如图,在正方形ABCD中,E为AD上的点,连接CE.①以点E为圆心,以任意长为半径作弧分别交EC,ED于点N,M;②分别以M,N为圆心,以大于 长为半径作弧,两弧在 内交于点P;③连接EP并延长交DC于点H,交BC的延长线于点G.若 , ,则EH的长为( )
A、△AFD B、△FED C、△AED D、不能确定10. 如图,在正方形ABCD中,E为AD上的点,连接CE.①以点E为圆心,以任意长为半径作弧分别交EC,ED于点N,M;②分别以M,N为圆心,以大于 长为半径作弧,两弧在 内交于点P;③连接EP并延长交DC于点H,交BC的延长线于点G.若 , ,则EH的长为( ) A、14 B、 C、16 D、
A、14 B、 C、16 D、二、填空题
-
11. 已知 ,它们的周长分别为 和 ,则 与 面积之比为.12.
如图,AB⊥CB于点B , AC⊥CD于点C , AB=6,AC=10,当CD= 时,△ABC∽△ACD .
 13. 如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是米(平面镜的厚度忽略不计).
13. 如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是米(平面镜的厚度忽略不计).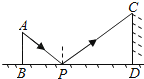 14. 如图,平行四边形 中,点 在边 上, 交 于点 ,如果 ,那么 的值是.
14. 如图,平行四边形 中,点 在边 上, 交 于点 ,如果 ,那么 的值是. 15. 如图,在▱ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF= .
15. 如图,在▱ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF= . 16. 如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是 .
16. 如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是 .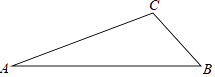
三、综合题
-
17. 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
 (1)、求证:直线DF与⊙O相切;
(1)、求证:直线DF与⊙O相切;
(2)、若AE=7,BC=6,求AC的长.18.(1)、计算: ÷ ;(2)、如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG. 19. 已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且 =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
19. 已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且 =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.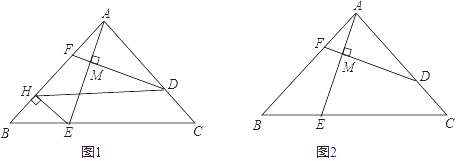 (1)、如图1,过点E作EH⊥AB于点H,连结DH.
(1)、如图1,过点E作EH⊥AB于点H,连结DH.①求证:四边形DHEC是平行四边形;
②若m= ,求证:AE=DF;
(2)、如图2,若m= ,求 的值.20. 如图,抛物线y= x2+bx+c与直线y= x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).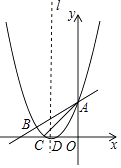 (1)、求抛物线的解析式;(2)、在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)、点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)、点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.