初数浙教版九上圆 专项复习(困难版)
试卷更新日期:2021-12-22 类型:复习试卷
一、单选题
-
1. 如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD长( )
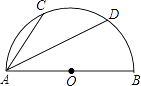 A、4 cm B、3 cm C、5 cm D、4 cm2. 如图,在半径为 的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
A、4 cm B、3 cm C、5 cm D、4 cm2. 如图,在半径为 的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )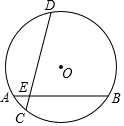 A、2 B、2 C、2 D、43. 如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于( )
A、2 B、2 C、2 D、43. 如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于( )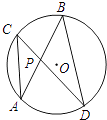 A、30° B、35° C、40° D、50°4. 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
A、30° B、35° C、40° D、50°4. 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )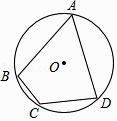 A、 B、 C、 D、5. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A、 B、 C、 D、5. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )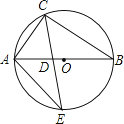 A、1: B、1: C、1:2 D、2:36. 如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N.欧儿里得在《几何原本》中利用该图解释了 .现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1 , 图中阴影部分的面积为S2 . 若点A,L,G在同一直线上,则 的值为( )
A、1: B、1: C、1:2 D、2:36. 如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N.欧儿里得在《几何原本》中利用该图解释了 .现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1 , 图中阴影部分的面积为S2 . 若点A,L,G在同一直线上,则 的值为( )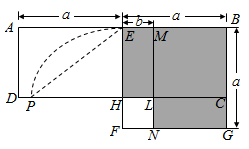 A、 B、 C、 D、7. 如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , ,将 沿直线 折叠,得到 ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是( )
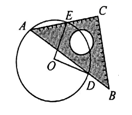
A、 B、 C、 D、7. 如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , ,将 沿直线 折叠,得到 ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是( )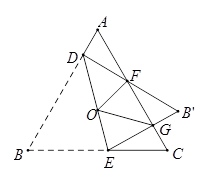 A、 B、 的周长是一个定值 C、四边形 的面积是一个定值 D、四边形 的面积是一个定值8. 如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
A、 B、 的周长是一个定值 C、四边形 的面积是一个定值 D、四边形 的面积是一个定值8. 如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )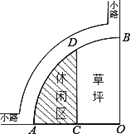
A、米2 B、米2 C、米2 D、米29. 已知正方形ABCD的边长为2,点E为正方形所在平面内一点,满足∠AED=90°,连接CE,若点F是CE的中点,则BF的最小值为( ) A、2 B、 -1 C、 D、210. 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
A、2 B、 -1 C、 D、210. 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( ) A、π B、 C、3+π D、8﹣π
A、π B、 C、3+π D、8﹣π二、填空题
-
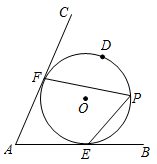
11. 如图,⊙O分别切∠BAC的两边AB,AC于点E,F,点P在优弧 上.若∠BAC=66°,则∠EPF等于度.
 12. 如图,在⊙O中,弦 ,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .
12. 如图,在⊙O中,弦 ,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .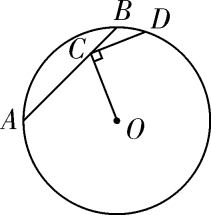 13.
13.如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E.则∠DOE的度数为.
 14. 如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=(k≠0)的图象经过圆心P,则k= .
14. 如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=(k≠0)的图象经过圆心P,则k= .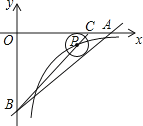 15. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为。
15. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为。 16. 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于 .
16. 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于 .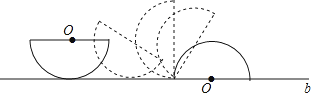
三、综合题
-
17. 已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
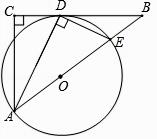 (1)、求证:BC是⊙O的切线;(2)、若AC=3,BC=4,求BE的长.18. 如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)、求证:BC是⊙O的切线;(2)、若AC=3,BC=4,求BE的长.18. 如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E. (1)、求证:DE是⊙O的切线.(2)、若DE= ,∠C=30°,求 的长。19. 如图, 是 的内接三角形,点 在 上,点 在弦 上( 不与 重合),且四边形 为菱形.
(1)、求证:DE是⊙O的切线.(2)、若DE= ,∠C=30°,求 的长。19. 如图, 是 的内接三角形,点 在 上,点 在弦 上( 不与 重合),且四边形 为菱形.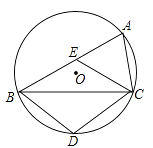 (1)、 求证: ;(2)、 求证: ;(3)、已知 的半径为3.
(1)、 求证: ;(2)、 求证: ;(3)、已知 的半径为3.①若 ,求 的长;
②当 为何值时, 的值最大?
20. 如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点. (1)、求抛物线的解析式;(2)、求证:ED是⊙P的切线;(3)、若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线y=ax2+bx+c上吗?请说明理由;(4)、若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、求证:ED是⊙P的切线;(3)、若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线y=ax2+bx+c上吗?请说明理由;(4)、若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.