初数浙教版九上圆 专项复习(普通版)
试卷更新日期:2021-12-22 类型:复习试卷
一、单选题
-
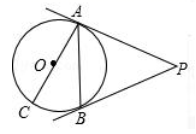
1. 已知 的半径为5,点 在 内,则 的长可能是( )A、7 B、6 C、5 D、42. 下列图形中, 为圆心角的是( )A、
 B、
B、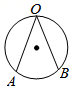 C、
C、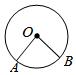 D、
D、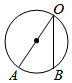 3. 同一平面内, 一个点到圆的最小距离为 , 最大距离为 , 则该圆的半径为 ( )A、 或 B、 或 C、 或 D、 或4. 如图,以AB为直径的半圆上有一点C,∠C=25°,则 的度数为( )
3. 同一平面内, 一个点到圆的最小距离为 , 最大距离为 , 则该圆的半径为 ( )A、 或 B、 或 C、 或 D、 或4. 如图,以AB为直径的半圆上有一点C,∠C=25°,则 的度数为( )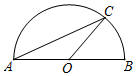 A、25° B、30° C、50° D、65°5. 如图,四边形ABCD内接于 ,如果它的一个外角 ,那么 的度数为( )
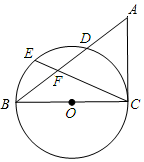
A、25° B、30° C、50° D、65°5. 如图,四边形ABCD内接于 ,如果它的一个外角 ,那么 的度数为( )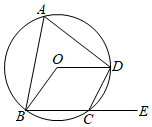 A、64° B、128° C、20° D、116°6. 一个形如圆锥冰淇淋纸筒,其底面直径为6cm,母线长为10cm,围成这样的冰淇淋纸筒所需纸的面积是( )A、60πcm2 B、15πcm2 C、28πcm2 D、30πcm27. 在 中, , , 把 绕点A顺时针旋转 后,得到 ,如图所示,则点B所走过的路径长为
A、64° B、128° C、20° D、116°6. 一个形如圆锥冰淇淋纸筒,其底面直径为6cm,母线长为10cm,围成这样的冰淇淋纸筒所需纸的面积是( )A、60πcm2 B、15πcm2 C、28πcm2 D、30πcm27. 在 中, , , 把 绕点A顺时针旋转 后,得到 ,如图所示,则点B所走过的路径长为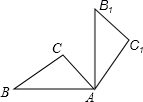 A、 B、 C、 D、8. 如图, 为 的直径,点 是弧 的中点.过点 作 于点 ,交 于点 ,若 , ,则 的半径长是( )
A、 B、 C、 D、8. 如图, 为 的直径,点 是弧 的中点.过点 作 于点 ,交 于点 ,若 , ,则 的半径长是( ) A、5 B、6.5 C、7.5 D、89. 正六边形的边长为 ,则它的面积为( )A、 B、 C、 D、10. 往水平放置的半径为 的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度 ,则水的最大深度为( )
A、5 B、6.5 C、7.5 D、89. 正六边形的边长为 ,则它的面积为( )A、 B、 C、 D、10. 往水平放置的半径为 的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度 ,则水的最大深度为( )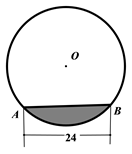 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,AB是半圆的直径,O是圆心, ,则∠ABC=°.
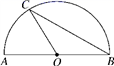 12. 一个正n边形的每一外角都等于60°,则n的值是.13. 如图,⊙O的直径CD=10,弦AB=8,AB⊥CD,垂足为M,则CM的长为.
12. 一个正n边形的每一外角都等于60°,则n的值是.13. 如图,⊙O的直径CD=10,弦AB=8,AB⊥CD,垂足为M,则CM的长为.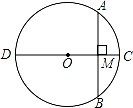 14. 一圆锥的母线长为6cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径r=cm.15. 如图, 是 的直径,点 在 上,若 ,则 °.
14. 一圆锥的母线长为6cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径r=cm.15. 如图, 是 的直径,点 在 上,若 ,则 °. 16. 如图,一把折扇展开后的圆心角为120°,扇骨 长为 ,扇面宽 ,则该折扇的扇面的面积 .
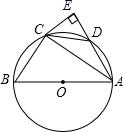
16. 如图,一把折扇展开后的圆心角为120°,扇骨 长为 ,扇面宽 ,则该折扇的扇面的面积 . 17. 如图,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在 上,边AB、AC分别交 于D、E两点﹐点B是 的中点,则∠ABE=.
17. 如图,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在 上,边AB、AC分别交 于D、E两点﹐点B是 的中点,则∠ABE=.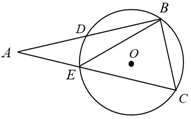 18. 如图,AB是半圆O的直径,AC=AD,OC=2, ∠CAB=30°.则点O到CD的距离OE为.
18. 如图,AB是半圆O的直径,AC=AD,OC=2, ∠CAB=30°.则点O到CD的距离OE为.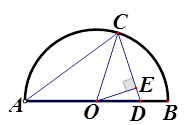
三、综合题
-
19. 如图,在△ABC中,点D是AC边上一点,以AD为直径的⊙O与边BC切于点E,且AB=BE.
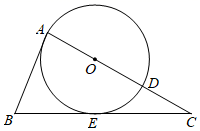 (1)、求证:AB是⊙O的切线;(2)、若BE=3,BC=7,求⊙O的半径长;(3)、求证: =CD•CA.
(1)、求证:AB是⊙O的切线;(2)、若BE=3,BC=7,求⊙O的半径长;(3)、求证: =CD•CA.