初数浙教版九上概率的简单应用 专项复习（普通版）
试卷更新日期：2021-12-22 类型：复习试卷
一、单选题
-
1. 为了防控疫情，学校决定从三位老师中（含甲老师）随机抽调2人去值周查体温，则甲老师被抽调去值周的概率是（ ）A、 B、 C、 D、2. 同时掷两枚质地均匀的骰子，则两枚骰子向上的点数之和为7的概率是（ ）A、 B、 C、 D、3. 学校招募运动会广播员，从两名男生和两名女生共四名候选人中随机选取两人，则两人恰好是一男一女的概率是（ ）A、 B、 C、 D、4. 育种小组对某品种小麦发芽情况进行测试，在测试基本情况相同的条件下，得到如下数据：
抽查小麦粒数
100
500
1000
2000
3000
4000
发芽粒数
95
486
968
1940
2907
则a的值最有可能是（ ）
A、3680 B、3720 C、3880 D、39605. 某班学生做“用频率估计概率”的实验时，给出的某一结果出现如图所示的统计图，则符合这一结果的实验可能是（ ）
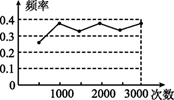A、抛一枚硬币，出现正面朝上 B、从标有1，2，3，4，5，6的六张卡片中任抽一张，出现偶数 C、从一个装有6个红球和3个黑球的袋子中任取一球，取到的是黑球 D、先后两次掷一枚质地均匀的正六面体骰子，两次向上的点数之和是76. 在一只不透明的口袋中放入红球5个，黑球1个，黄球n个，这些球除颜色不同外，其它无任何差别.搅匀后随机从中摸出一个恰好是黄球的概率为 ，则放入口袋中的黄球总数n是（ ）A、3 B、4 C、5 D、67. 某轨道列车共有3节车厢，设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车，则甲和乙从同一节车厢上车的概率是（ ）A、 B、 C、 D、8. 为了估计某地区梅花鹿的数量，先捕捉20只梅花鹿做上标记，然后放走，待有标记的梅花鹿完全混合于鹿群后，第二次捕捉100只梅花鹿，发现其中5只有标记．估计这个地区的梅花鹿的数量约有（ ）只．A、200 B、300 C、400 D、500二、填空题
-
9. 在一个不透明的袋子中有50个除颜色外均相同的小球，通过多次摸球试验后，发现摸到白球的频率约为36%，估计袋中白球有个.10. 某林业部门要考察某种幼树在一定条件下的移植成活率，在同样的条件下对这种幼树进行大量移植，并统计成活情况，记录如下:
移植总数（n）
50
200
1000
5000
10000
成活（m）
46
171
912
4480
9020
成活的频率（ ）
0.920
0.855
0.912
0.896
0.902
由此可以估计幼树移植成活的概率为（结果保留小数点后一位）
11. 一个不透明的口袋中有红球和黑球共若干个，这些球除颜色外都相同，每次摸出1个球，进行大量的摸球试验后，发现摸到黑球的频率在0.4附近摆动，据此估计摸到红球的概率为。12. 现有四张正面分别标有数字 的卡片，它们除数字不同外，其余完全相同，将卡片背面朝上洗匀后，从中随机取出一张，再从剩下的卡片中随机取出一张，则两次取出的卡片上的数字之和为负数的概率为.13. 某市对一批口罩进行抽检，统计合格口罩的只数，得到口罩的合格频率如下：抽检只数（只）
50
100
150
500
1 000
2 000
10 000
50 000
合格频率
0.82
0.83
0.82
0.83
0.84
0.84
0.84
0.84
则从该批口罩中任抽一只口罩，是合格品的概率约为.
14. 看了《田忌赛马》故事后，小杨用数学模型来分析齐王与田忌的上中下三个等级的三匹马记分如表，每匹马只赛一场，两数相比，大数为胜，三场两胜则赢．已知齐王的三匹马出场顺序为10，8，6．若田忌的三匹马随机出场，则田忌能赢得比赛的概率为 ．马匹
姓名
下等马
中等马
上等马
齐王
6
8
10
田忌
5
7
9
三、综合题
-
15. 对一批衬衣进行抽检，统计合格衬衣的件数，获得如下频数表.
抽取件数（件）
100
150
200
500
800
1000
合格频数
88
141
176
445
720
900
合格频率
______
0.94
0.88
0.89
0.90
______
(1)、完成上表.(2)、估计任意抽一件衬衣是合格品的概率.(3)、估计出售1200件衬衣，其中次品大约有几件.16. 某单位食堂为全体960名职工提供了A，B，C，D四种套餐，为了解职工对这四种套餐的喜好情况，单位随机抽取240名职工进行“你最喜欢哪一种套餐（必选且只选一种）”问卷调查.根据调查结果绘制了条形统计图和扇形统计图，部分信息如下：
(1)、在抽取的240人中最喜欢A套餐的人数为 ， 扇形统计图中“C”对应扇形的圆心角的大小为°；(2)、依据本次调查的结果，估计全体960名职工中最喜欢B套餐的人数；(3)、现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”，求甲被选到的概率.17. 现有一张演唱会的门票，小明与小华为了决定谁拿这张门票去看开幕式，小华设计了一种方案如下：如图，有 、 两个转盘，其中转盘 被分成3等份，转盘 被分成4等份，并在每一份内标上数字.两人同时分别转动其中一个转盘，转盘停止后（当指针指在边界线上时视为无效，重转），若将 转盘指针指向的数字记为 ， 转盘指针指向的数字记为 ，从而确定点 的坐标为 .
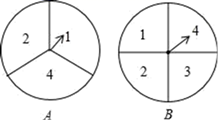(1)、请用列表或画树状图的方法写出所有可能得到的点 的坐标；(2)、小华提议，在（1）的基础上，若点 落在反比例函数 图象上则小明赢；否则，自己赢.你觉得小华的提议对双方公平吗？请说明理由.18. 甲、乙两人进行摸牌游戏：有三张形状大小完全相同的牌，正面分别标有数字2，3，5。现将三张牌背面朝上，洗匀后放在桌子上。(1)、甲从中随机抽一张牌，记录数字后放回洗匀，乙再随机抽取一张.请用列表或画树状图的方法，求两人抽取的数字相同的概率.(2)、若两人抽取的数字之和为2的倍数，则甲获胜；若抽取的数字之和为5的倍数，则乙获胜，这个游戏公平吗？请用概率的知识加以解释.