初数浙教版九上二次函数的实际应用 专项复习(困难版)
试卷更新日期:2021-12-22 类型:复习试卷
一、单选题
-
1. 某种商品的价格是 元,准备进行两次降价.如果每次降价的百分率都是 ,经过两次降价后的价格 (单位:元)随每次降价的百分率 的变化而变化,则 关于 的函数解析式是( )A、 B、 C、 D、2. 如图,四边形ABCD中,AB=AD , CE⊥BD , CE= BD . 若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是( )
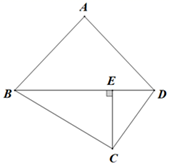 A、 B、 C、 D、3. 如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为 ,则小球从飞出到落地的所用时间为
A、 B、 C、 D、3. 如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为 ,则小球从飞出到落地的所用时间为 A、 B、 C、 D、4. 有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( )
A、 B、 C、 D、4. 有一拱桥洞呈抛物线形,这个桥洞的最大高度是16m,跨度为40m,现把它的示意图(如图)放在坐标系中,则抛物线的解析式为( ) A、y= x2+ x B、y=- x2+ x C、y=- x2- x D、y=- x2+ x+165. 如图,等边三角形 中, ,动点 从点 出发,以每秒2个单位的速度沿折线 的路径向点 运动,同时动点 也从点 出发,沿线段 以每秒1个单位的速度向点 运动,连接 ,设点 , 的运动时间为 , 的面积为 ,则能反映 与 之间函数关系的图象是( )
A、y= x2+ x B、y=- x2+ x C、y=- x2- x D、y=- x2+ x+165. 如图,等边三角形 中, ,动点 从点 出发,以每秒2个单位的速度沿折线 的路径向点 运动,同时动点 也从点 出发,沿线段 以每秒1个单位的速度向点 运动,连接 ,设点 , 的运动时间为 , 的面积为 ,则能反映 与 之间函数关系的图象是( )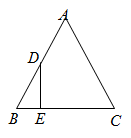 A、
A、 B、
B、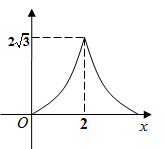 C、
C、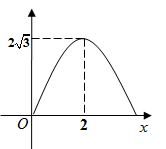 D、
D、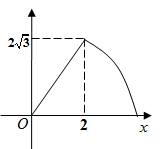 6. 如图,抛物线与 轴交于 , 两点,点 从点 出发,沿抛物线向点 匀速运动,到达点 停止,设运动时间为 秒,当 和 时, 的值相等.有下列结论:① 时, 的值最大;② 时,点 停止运动;③当 和 时, 的值不相等;④ 时, .其中正确的是( )
6. 如图,抛物线与 轴交于 , 两点,点 从点 出发,沿抛物线向点 匀速运动,到达点 停止,设运动时间为 秒,当 和 时, 的值相等.有下列结论:① 时, 的值最大;② 时,点 停止运动;③当 和 时, 的值不相等;④ 时, .其中正确的是( ) A、①④ B、②④ C、①③ D、②③
A、①④ B、②④ C、①③ D、②③二、填空题
-
7. 退休的李老师借助自家15米的院墙和总长度为30米的围栏,在院墙外设计一个矩形花圃种植花草.为方便进出,他在如图所示的位置安装了一个1米宽的门,如果设和墙相邻的一边长为x米,花圃面积为y平方米,则y与x之间的函数关系式为 .
 8. 如图,某大门的形状是一抛物线形建筑,大门的地面宽8m,在两侧距地面3.5m高处有两个挂单位名牌匾用的铁环,两铁环的水平距离是6m.若按图所示建立平面直角坐标系,则抛物线的解析式是 . (建筑物厚度忽略不计)
8. 如图,某大门的形状是一抛物线形建筑,大门的地面宽8m,在两侧距地面3.5m高处有两个挂单位名牌匾用的铁环,两铁环的水平距离是6m.若按图所示建立平面直角坐标系,则抛物线的解析式是 . (建筑物厚度忽略不计)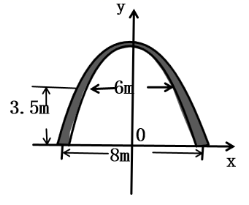 9. 如图,二次函数y=x2-2x+c的图象与x轴交于点A(3,0),点D是y轴负半轴上一点,以OA,OD为邻边作矩形ABDO,直线BD交二次函数的图象于点C,E(点C在点D的左侧),若CD=BE,则OD的长为 .
9. 如图,二次函数y=x2-2x+c的图象与x轴交于点A(3,0),点D是y轴负半轴上一点,以OA,OD为邻边作矩形ABDO,直线BD交二次函数的图象于点C,E(点C在点D的左侧),若CD=BE,则OD的长为 . 10. 用长为 的铝合金制成如图所示形状的矩形窗框 ,当 m时窗户的透光面积最大(铝合金条遮光部分忽略不计).
10. 用长为 的铝合金制成如图所示形状的矩形窗框 ,当 m时窗户的透光面积最大(铝合金条遮光部分忽略不计). 11. 如图,点A是抛物线y=x2﹣4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为.
11. 如图,点A是抛物线y=x2﹣4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为. 12. “水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图 1 所示,碗体 DEC 呈抛物线状(碗体厚度不计),点 E 是抛物线的顶点,碗底高 EF=1cm,碗底宽 AB=2 cm,当瓷碗中装满面汤时,液面宽 CD=83cm,此时面汤最大深度 EG=6cm,将瓷碗绕点 B 缓缓倾斜倒出部分面汤,如图2,当 LABK=30 时停止,此时液面 CH 到桌面的距离为cm;碗内面汤的最大深度是cm.
12. “水晶晶南浔”的美食文化中以特有的双交面出名,盛面的瓷碗截面图如图 1 所示,碗体 DEC 呈抛物线状(碗体厚度不计),点 E 是抛物线的顶点,碗底高 EF=1cm,碗底宽 AB=2 cm,当瓷碗中装满面汤时,液面宽 CD=83cm,此时面汤最大深度 EG=6cm,将瓷碗绕点 B 缓缓倾斜倒出部分面汤,如图2,当 LABK=30 时停止,此时液面 CH 到桌面的距离为cm;碗内面汤的最大深度是cm. 13. 已知抛物线 与x轴交于A , B两点,对称轴与抛物线交于点C , 与x轴交于点D , ⊙C的半径为1,G为⊙C上一动点,P为AG的中点,则DP的最大值为.
13. 已知抛物线 与x轴交于A , B两点,对称轴与抛物线交于点C , 与x轴交于点D , ⊙C的半径为1,G为⊙C上一动点,P为AG的中点,则DP的最大值为.
 14. 已知:如图,直线y=kx+b(k , b为常数)分别与x轴、y轴交于点A(﹣4,0),B(0,3),抛物线y=﹣x2+4x+1与y轴交于点C , 点E在抛物线y=﹣x2+4x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是 .
14. 已知:如图,直线y=kx+b(k , b为常数)分别与x轴、y轴交于点A(﹣4,0),B(0,3),抛物线y=﹣x2+4x+1与y轴交于点C , 点E在抛物线y=﹣x2+4x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是 .
三、综合题
-
15. “互联网 ”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、求y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出400元资助贫困学生.为了保证捐款后每月利润不低于4020元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?直接写出销售单价.16. 某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件,第二个月如果单价不变,预计仍可以售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降10元,可多售出100件,但最低单价应高于购进的价格;第二月结束后.批发商核对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.(1)、填表(不需化简)
时间
第一个月
第二个月
清仓时
单价(元)
80
40
销售量
200
(2)、如果批发商希望通过销售这批T恤获利8750元,那么第二个月的单价应该是多少?(3)、如果批发商希望通过销售这批T恤获利最大,那么最大利润可达到多少元?(直接写出答案)17. 自2020年3月开始,我国生猪、猪肉价格持续上涨,某大型菜场在销售过程中发现,从2020年10月1日起到11月9日的40天内,猪肉的每千克售价与上市时间的关系用图1的一条折线表示:猪肉的进价与上市时间的关系用图2的一段抛物线 表示. (1)、 ;(2)、求图1表示的售价P与时间x的函数关系式;(3)、问从10月1日起到11月9日的40天内第几天每千克猪肉利润最低,最低利润为多少?18. 女生排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某女生在O处将球垫偏,之后又在A, B两处先后垫球,球沿抛物线C1 → C2 → C3运动(假设抛物线C1 , C2 , C3在同一平面内),最终正好在O处垫住,O处离地面的距离为1米.如图所示,以O为坐标原点1米为单位长度建立直角坐标系,x轴平行于地面水平直线m,已知点A( , ),点B的横坐标为 - ,抛物线C1和C3的表达式分别为 y = ax2- 2ax 和 y = 2ax2 + bx (a≠ 0).
(1)、 ;(2)、求图1表示的售价P与时间x的函数关系式;(3)、问从10月1日起到11月9日的40天内第几天每千克猪肉利润最低,最低利润为多少?18. 女生排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某女生在O处将球垫偏,之后又在A, B两处先后垫球,球沿抛物线C1 → C2 → C3运动(假设抛物线C1 , C2 , C3在同一平面内),最终正好在O处垫住,O处离地面的距离为1米.如图所示,以O为坐标原点1米为单位长度建立直角坐标系,x轴平行于地面水平直线m,已知点A( , ),点B的横坐标为 - ,抛物线C1和C3的表达式分别为 y = ax2- 2ax 和 y = 2ax2 + bx (a≠ 0).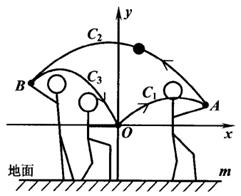 (1)、求抛物线C1的函数表达式.(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由.(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处B 离地面的高度至少为多少米?
(1)、求抛物线C1的函数表达式.(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由.(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处B 离地面的高度至少为多少米?