初数浙教版九上二次函数的实际应用 专项复习(普通版)
试卷更新日期:2021-12-22 类型:复习试卷
一、单选题
-
1.
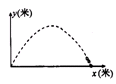
某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是 ( )
 A、4米 B、3米 C、2米 D、1米2. 河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为y=﹣x2 , 当水面离桥拱顶的高度DO是4m时,这时水面宽度AB为( )
A、4米 B、3米 C、2米 D、1米2. 河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为y=﹣x2 , 当水面离桥拱顶的高度DO是4m时,这时水面宽度AB为( ) A、﹣20m B、10m C、20m D、﹣10m3. 如图,一边靠学校院墙,其它三边用 40 米长的篱笆围成一个矩形花圃,设矩形 ABCD 的边 AB=x 米,面积为 S 平方米,则下面关系式正确的是( )
A、﹣20m B、10m C、20m D、﹣10m3. 如图,一边靠学校院墙,其它三边用 40 米长的篱笆围成一个矩形花圃,设矩形 ABCD 的边 AB=x 米,面积为 S 平方米,则下面关系式正确的是( ) A、
A、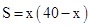 B、
B、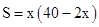 C、
C、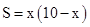 D、
D、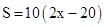 4. 某种商品的进货检为每件a元,零售价为每件90元,若商品按八五折出售,仍可获利10%,则下列方程正确的是( )A、85%a10%×90 B、90×85%×10%=a C、85%(90﹣a)=10% D、(1+10%)a=90×85%5. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
4. 某种商品的进货检为每件a元,零售价为每件90元,若商品按八五折出售,仍可获利10%,则下列方程正确的是( )A、85%a10%×90 B、90×85%×10%=a C、85%(90﹣a)=10% D、(1+10%)a=90×85%5. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )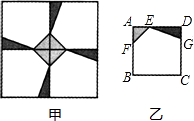 A、
A、 B、
B、 C、
C、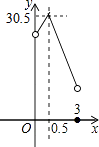 D、
D、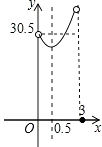 6. 将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,若这种商品的零售价每降价1元,其日销量就增加1个,为了获取每日最大利润,则应降价( )
6. 将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,若这种商品的零售价每降价1元,其日销量就增加1个,为了获取每日最大利润,则应降价( )
A、5元 B、10元 C、15元 D、20元7. 如图,在 中, , , ,动点 从点 开始沿 向点以 以 的速度移动,动点 从点 开始沿 向点 以 的速度移动.若 , 两点分别从 , 两点同时出发, 点到达 点运动停止,则 的面积 随出发时间 的函数关系图象大致是( )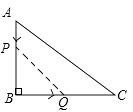 A、
A、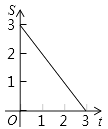 B、
B、 C、
C、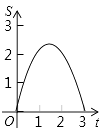 D、
D、 8. 如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是( )
8. 如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是( ) A、18m2 B、 m2 C、 m2 D、 m29. 喜迎圣诞,某商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价每上涨1元,则每星期就会少卖出10件.设每件商品的售价上涨x元(x正整数),每星期销售该商品的利润为y元,则y与x的函数解析式为( )A、y=﹣10x2+100x+2000 B、y=10x2+100x+2000 C、 y=﹣10x2+200x D、y=﹣10x2﹣100x+200010. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
A、18m2 B、 m2 C、 m2 D、 m29. 喜迎圣诞,某商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价每上涨1元,则每星期就会少卖出10件.设每件商品的售价上涨x元(x正整数),每星期销售该商品的利润为y元,则y与x的函数解析式为( )A、y=﹣10x2+100x+2000 B、y=10x2+100x+2000 C、 y=﹣10x2+200x D、y=﹣10x2﹣100x+200010. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t= ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
11. 某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 .12. 小明推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系为y=﹣ +3,则小明推铅球的成绩是m.
13. 某软件商品销售一种益智游戏软件,如果以每盘50元的售价销售,一个月能售出500盘,根据市场分析,若销售单价每涨价1元,月销售量就减少10盘,试写出当每盘的售价涨x元时,该商店月销售额y(元)与x(元)的函数关系式为 .14. 在半径为4cm的圆中,挖去一个半径为x(cm)的圆面,剩下一个圆环的面积为y(cm2),则y与x的函数关系式为 , 其中自变量x的取值范围是 .15. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为cm.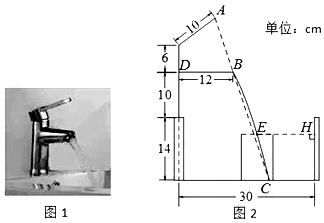 16. 两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了m,恰好把水喷到F处进行灭火.
16. 两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了m,恰好把水喷到F处进行灭火.
三、综合题
-
17. 某花圃销售一批名贵花卉,平均每天可售出20盆,每盆盈利40元,为了增加盈利并尽快减少库存,花圃决定采取适当的降价措施,经调查发现,如果每盆花卉每降1元,花圃平均每天可多售出2盆.(1)、若花圃平均每天要盈利1200元,每盆花卉应降价多少元?(2)、每盆花卉降低多少元时,花圃平均每天盈利最多,是多少?18. 某广告公司设计一幅周长为12m的矩形广告牌,广告设计费为每平方米1000元,设矩形的一边长为x m,所花费用为y元.(1)、请你写出y与x之间的函数表达式,写出x的取值范围;(2)、估计当x取何值时,y有最大设计费用.19. 永嘉某商店试销一种新型节能灯,每盏节能灯进价为18元,试销过程中发现,每周销量y(盏)与销售单价x(元)之间关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣进价)
(1)、写出每周的利润w(元)与销售单价x(元)之间函数解析式;
(2)、当销售单价定为多少元时,这种节能灯每周能够获得最大利润?最大利润是多少元?
(3)、物价部门规定,这种节能灯的销售单价不得高于30元.若商店想要这种节能灯每周获得350元的利润,则销售单价应定为多少元?20. 某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.(1)、求该种水果每次降价的百分率;(2)、从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?时间x(天)
1≤x<9
9≤x<15
x≥15
售价(元/斤)
第1次降价后的价格
第2次降价后的价格
销量(斤)
80﹣3x
120﹣x
储存和损耗费用(元)
40+3x
3x2﹣64x+400
(3)、在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?