初数浙教版九上待定系数法求二次函数解析式及根的问题专项复习（困难版）

试卷更新日期：2021-12-22 类型：复习试卷

进入出卷网下载

一、单选题

1. 若二次函数y=ax²（a≠0）的图象过点（-2，-3），则必在该图象上的点还有（）

A、(-3，-2) B、(2，3) C、(2，3) D、(-2，3)

查看试题解析
2. 如图，抛物线y＝ax²+bx+3（a≠0）的对称轴为直线x＝1，如果关于x的方程ax²+bx﹣6＝0（a≠0）的一个根为2，那么该方程的另一个根为（）

A、﹣2 B、﹣1 C、0 D、3

查看试题解析
3. 若函数y=ax²+bx的图象如图所示，则关于x的一元二次方程ax²+bx+5=0的根的情况为（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
4. 如图，若二次函数y=ax²+bx+c(a≠0)图象的对称轴为直线x=1，与y轴交于点C，与x轴交于点A，点B(-1，0)，给出下列结论：其中正确的个数是（）

①当x>0时，y随x的增大而减小；②am²+bm+c<a+b+c (m≠l)；③b²-4ac<0；④当y>0时，-1<x<3；⑤2a+c>0

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 顶点(﹣5，﹣1)，且开口方向、形状与函数y＝ $\frac{1}{3}$ x²的图象相同的抛物线是（　　）

A、 $y = \frac{1}{3} x^{2} - 5$ B、 $y = \frac{1}{3} {(x - 5)}^{2} + 1$ C、 $y = \frac{1}{3} {(x - 5)}^{2} - 1$ D、 $y = \frac{1}{3} {(x + 5)}^{2} - 1$

查看试题解析
6. 如图所示二次函数y＝ax²+bx+c的图象的一部分，图象过点（﹣3，0），对称轴为直线x＝﹣1，以下结论：①2a﹣b＝0；②abc＜0；③当﹣3＜x＜1时，y＞0；④对于a的每一个确定值，若一元二次方程ax²+bx+c＝t（t为常数，t≥0）的根为整数，则t的值只有3个.其中正确的有（　　）

A、4个 B、3个 C、2个 D、1个

查看试题解析

7. 已知二次函数

y = a x^{2} + b x + c

，其函数值y与自变量x之间的部分对应值如表所示：

x	…	0	1	2	3	…
y	…	1	2	1	-2	…

则方程 $a x^{2} + b x + c = 0$ 的正数解 $x_{0}$ 在下列哪个范围内（）

A、

0 < x_{0} \leq 1

B、

1 < x_{0} \leq 2

C、

2 < x_{0} \leq 3

D、

x_{0} > 3

查看试题解析

8. 如图，动点A在抛物线y＝﹣x²+2x+3（0≤x≤3）上运动，直线l经过点（0，6），且与y轴垂直，过点A作AC⊥l于点C，以AC为对角线作矩形ABCD，则另一对角线BD的取值范围正确的是（　　）

A、2≤BD≤3 B、3≤BD≤6 C、1≤BD≤6 D、2≤BD≤6

查看试题解析
9. 三个关于 $x$ 的方程： $a_{1} {(x+1)(x-2)=1，a}_{2} {(x+1)(x-2)=1，a}_{3} (x+1)(x-2)=1$ ，已知常数 $a_{1} {>a}_{2} {>a}_{3} >0$ ，若 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 分别是按上顺序对应三个方程的正根，则下列判断正确的是（ )

A、 $x_{1} {<x}_{2} {<x}_{3}$ B、 $x_{1} > x_{2} > x_{3}$ C、 $x_{1} = x_{2} = x_{3}$ D、不能确定 $x_{1} 、 x_{2} 、 x_{3}$ 的大小

查看试题解析
10. 已知抛物线 $y = a x^{2} + b x + c$ 如图所示，则有：
① $a b c < 0$ ；

② $b < a + c$ ；

③ $4 a + 2 b + c > 0$ ；

④ $2 c > 3 b$ ；

⑤ $a + b > m (m a + b) (m \neq 1)$

其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

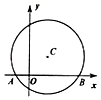
11. 请写出一个开口向下，并且与 $y$ 轴交于点 $(0 ， 4)$ 的抛物线的解析式．

查看试题解析
12. 已知次函数 $y = x^{2} + 2 x - 1$ 的一个函数值是2，那么对应的自变量x的值是．

查看试题解析
13. 二次函数y= $2 x^{2} + 4 x + m$ 经过点（1，2），m=

查看试题解析
14. 二次函数y＝ax²+bx+c（a≠0）的图象经过（﹣1，0），（0，4），（t，4）三点，当t≥3时，一元二次方程ax²+bx+c＝n一定有实数根，则n的取值范围是．

查看试题解析
15. 如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A ， B两点，点P在 $\overset{⌢}{A B}$ 上．请写出经过A、B且以点P为顶点的抛物线解析式．

查看试题解析
16. 若抛物线y=ax²+bx+c与抛物线y=2x²-4x-1的顶点重合，且与y轴的交点的坐标为(0，1)，则抛物线y=ax²+bx+c的表达式是.

查看试题解析

三、综合题

17. 如图，已知二次函数y＝﹣x²＋bx＋c的图象经过点A（﹣2，0），B（6，0），与y轴交于点C．

(1)、求抛物线的解析式；

(2)、抛物线的对称轴上是否存在点P，使∠PAB＝∠ABC，若存在请直接写出点P的坐标，若不存在，请说明理由．

查看试题解析
18. 若抛物线的顶点坐标是（﹣4，3），且过点（﹣5，1）．

(1)、求此抛物线的函数关系式．

(2)、直接写出当﹣6＜x＜﹣1时，y的取值范围．

查看试题解析
19. 如图，已知二次函数 $y = - \frac{1}{2} x^{2} + 4 x + c$ 的图象经过A（2，0）.

(1)、求 $c$ 的值.

(2)、若二次函数于 $y$ 轴相交于的 $B$ 点，且该二次函数的对称轴与 $x$ 轴交于点 $C$ ，连结 $B A 、 B C$ ，求 $△ A B C$ 的面积.

查看试题解析
20. 在平面直角坐标系xOy中，抛物线y＝ax²＋bx＋c与y轴交于点C，其顶点记为M，自变量x＝﹣1和x＝5对应的函数值相等．若点M在直线l：y＝﹣12x＋16上，点（3，﹣4）在抛物线上．

(1)、求该抛物线的解析式；

(2)、直线l与抛物线另一交点记为B，Q为线段BM上一动点（点Q不与M重合）．设Q点坐标为（t，n），过Q作QH⊥x轴于点H，将以点Q，H，O，C为顶点的四边形的面积S表示为t的函数，标出自变量t的取值范围，并求出S可能取得的最大值．

查看试题解析

初数浙教版九上待定系数法求二次函数解析式及根的问题 专项复习（困难版）

一、单选题

二、填空题

三、综合题

初数浙教版九上待定系数法求二次函数解析式及根的问题专项复习（困难版）