初数浙教版九上待定系数法求二次函数解析式及根的问题 专题复习(普通版)
试卷更新日期:2021-12-22 类型:复习试卷
一、单选题
-
1. 若抛物线y=x2+bx+c的对称轴为y轴,且点P(2,6)在该抛物线上,则c的值为( )A、﹣2 B、0 C、2 D、42. 已知抛物线y=x2+x-1经过点P(m,5),则代数式m2+m+100的值为 ( )A、104 B、105 C、106 D、1073. 小敏在某次投篮中,球的运动路线是抛物线y=﹣ x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离L是( )
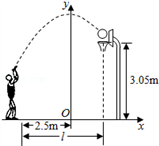 A、3.5m B、4m C、4.5m D、4.6m4. 下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
A、3.5m B、4m C、4.5m D、4.6m4. 下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:x
1
1.1
1.2
1.3
1.4
y
﹣1
﹣0.49
0.04
0.59
1.16
那么方程x2+3x﹣5=0的一个近似根是( )
A、1 B、1.1 C、1.2 D、1.35. 已知二次函数 的图象上有两点A(x1 , 2023)和B(x2 , 2023),则当 时,二次函数的值是( )A、2020 B、2021 C、2022 D、20236. 关于x的一元二次方程 (t为实数)有且只有一个根在 的范围内,则t的取值范围是( )A、 B、 C、 或 D、7. 二次函数y=ax2+bx+c(a , b , c为常数,且a≠0)中的x与y的部分对应值如表:x
…
﹣1
0
1
3
…
y
…
﹣1
3
5
3
…
下列结论错误的是( )
A、ac<0 B、3是关于x的方程ax2+(b﹣1)x+c=0的一个根 C、当x>1时,y的值随x值的增大而减小 D、当﹣1<x<3时,ax2+(b﹣1)x+c>08. 若抛物线y=ax2+bx+c与x轴两个交点之间的距离为10,且4a+b=0,则关于x的方程ax2+bx+c=0的根为( )A、x1=﹣7,x2=3 B、x1=﹣6,x2=4 C、x1=6,x2=﹣4 D、x1=7,x2=﹣39. 已知二次函数y=-x2+bx+c的顶点为(1,5),那么关于x的一元二次方程-x2+bx+c-4=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定10. 如图,平行于x轴的直线AC分别交函数 y =x (x≥0)与 y = x (x≥0)的图象于 B,C两点,过点C作y轴的平行线交y =x (x≥0)的图象于点D,直线DE∥AC交 y = x (x≥0)的图象于点E,则 =( )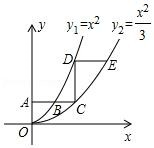 A、 B、1 C、 D、3﹣
A、 B、1 C、 D、3﹣二、填空题
-
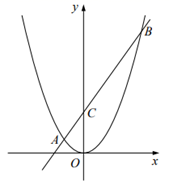
11. 如果抛物线经过点A(-1,0)和点B(5,0),那么这条抛物线的对称轴是直线12. 请写出一个开口向上,并且与 轴交于点 的抛物线解析式 .13. 二次函数 的图象经过原点,则 .14. 已知二次函数 的图象上有 , , 三个点.用“<”连接 , , 的结果是.15. 设抛物线 ,其中 为实数.(1)、若抛物线经过点 ,则 .(2)、将抛物线 向上平移2个单位,所得抛物线顶点的纵坐标的最大值是.16. 如图,在平面直角坐标系中,O为坐标原点,点C为y轴正半轴上的一个动点,过点C的直线与二次函数 的图象交于A、B两点,且 ,P为 的中点,设点P的坐标为 ,写出y关于x的函数表达式为:.
三、综合题
-
17. 已知抛物线 经过点(−1,8).(1)、求抛物线的解析式;(2)、求抛物线与x轴交点的坐标.18. 已知抛物线的顶点坐标为(-1,2),与y轴交于点(0, )(1)、求二次函数的解析式;(2)、判断点P(2,- )是否落在抛物线上,请说明理由.19. 如图,抛物线 与x轴交于A,B两点,与y轴交于点C,直线 经过点C.线段 在线段 上移动,点P的横坐标为t, ,分别过点P,Q作x轴的垂线,交抛物线于E,F两点,交直线 于D,G两点.
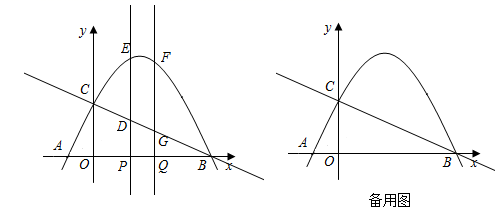 (1)、求抛物线的解析式;(2)、是否存在实数t,使得 ?如果存在,请求出相应的t的值;如果不存在,请说明理由.20. 如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x﹣3经过点B,C.
(1)、求抛物线的解析式;(2)、是否存在实数t,使得 ?如果存在,请求出相应的t的值;如果不存在,请说明理由.20. 如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x﹣3经过点B,C. (1)、求抛物线的解析式;(2)、点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.
(1)、求抛物线的解析式;(2)、点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.①线段PM是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.