初数浙教版九上二次函数三种形式和最值问题 专项复习(困难版)
试卷更新日期:2021-12-22 类型:复习试卷
一、单选题
-
1. 若二次函数 的图象如图所示,则一次函数 与反比例函数 在同一个坐标系内的大致图象为( )
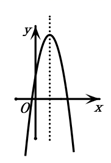 A、
A、 B、
B、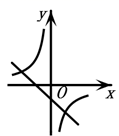 C、
C、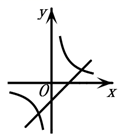 D、
D、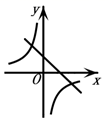 2. 如图,二次函数 ( )的图象与 轴交于点 ,其对称轴为直线 ,若 ,则下列结论中错误的是( )
2. 如图,二次函数 ( )的图象与 轴交于点 ,其对称轴为直线 ,若 ,则下列结论中错误的是( ) A、 B、 C、 D、3. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( )
A、 B、 C、 D、3. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( ) A、①② B、②③ C、①②④ D、②③④4. 点P(a,b)在以y轴为对称轴的二次函数y= +mx+5的图象上,则2a-b的最大值等于( )A、4 B、-4 C、-4.5 D、4.55. 已知函数 (a为常数),当 时,y随x增大而增大. 是该函数图象上的两点,对任意的 和 , 总满足 ,则实数a的取值范围是( )A、 B、 C、 D、6. 已知非负数 , , 满足 且 ,设 的最大值为 ,最小值为 ,则 的值是( )A、16 B、15 C、9 D、77. 在平面直角坐标系中,有两条抛物线关于原点中心对称,且它们的顶点相距 个单位长度,若其中一条抛物线的函数表达式为 ,则 的值为( )A、 或 B、 或 C、 或 D、 或8. 如图,在 中,点 是 边上任意一动点(点 与点 , 不重合),平行四边形 的顶点 , 分别在 , 上.已知 , .设 ,平行四边形 的面积为 ,当点 沿 方向运动时,则 的值( )
A、①② B、②③ C、①②④ D、②③④4. 点P(a,b)在以y轴为对称轴的二次函数y= +mx+5的图象上,则2a-b的最大值等于( )A、4 B、-4 C、-4.5 D、4.55. 已知函数 (a为常数),当 时,y随x增大而增大. 是该函数图象上的两点,对任意的 和 , 总满足 ,则实数a的取值范围是( )A、 B、 C、 D、6. 已知非负数 , , 满足 且 ,设 的最大值为 ,最小值为 ,则 的值是( )A、16 B、15 C、9 D、77. 在平面直角坐标系中,有两条抛物线关于原点中心对称,且它们的顶点相距 个单位长度,若其中一条抛物线的函数表达式为 ,则 的值为( )A、 或 B、 或 C、 或 D、 或8. 如图,在 中,点 是 边上任意一动点(点 与点 , 不重合),平行四边形 的顶点 , 分别在 , 上.已知 , .设 ,平行四边形 的面积为 ,当点 沿 方向运动时,则 的值( ) A、一直不变 B、一直变大 C、一直变小 D、有最大值19. 已知 的图象如图所示,对称轴为直线 ,若 , 是一元二次方程 的两个根,且 , ,则下列说法正确的是( )
A、一直不变 B、一直变大 C、一直变小 D、有最大值19. 已知 的图象如图所示,对称轴为直线 ,若 , 是一元二次方程 的两个根,且 , ,则下列说法正确的是( ) A、 B、 C、 D、10. 如图,抛物线y=ax2+bx+c与x轴的一个交点E在点(-3,0)和(-2,0)之间(包括这两点),顶点P是矩形ABCD上(包括边界和内部)的一个动点,则a的取值范围是( )
A、 B、 C、 D、10. 如图,抛物线y=ax2+bx+c与x轴的一个交点E在点(-3,0)和(-2,0)之间(包括这两点),顶点P是矩形ABCD上(包括边界和内部)的一个动点,则a的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 函数y=2x2-8x+1的最小值是.12. 已知,根据图1的 与 的关系,得到图2平面直角坐标系中的射线 和射线 .若点 是 轴上一点,过点 作 轴交 , 于点 , ,连结 , ,则 的比值为 , 的面积最大值为.
 13. 若二次函数y=x2﹣4x+2m的最小值是0,则m=.14. 如图,已知 ,在x轴上取 两点,使 ,把线段 交点A沿逆时针方向旋转 ,得线段 ,把线段 绕点B沿顺时针方向旋转 ,得线段 ,当 两点之间的距离最小时,点C的坐标为.
13. 若二次函数y=x2﹣4x+2m的最小值是0,则m=.14. 如图,已知 ,在x轴上取 两点,使 ,把线段 交点A沿逆时针方向旋转 ,得线段 ,把线段 绕点B沿顺时针方向旋转 ,得线段 ,当 两点之间的距离最小时,点C的坐标为.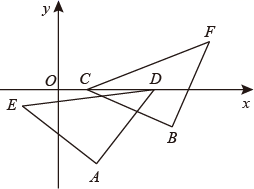 15. 对某条线段的长度进行了3次测量,得到3个结果(单位:mm)9.9,10.1,10.0,若用a作为这条线段长度的近似值,当10.0mm时,最小.对另一条线段的长度进行了n次测量,得到n个结果(单位:mm)x1 , x2 , …xn , 若用x作为这条线段长度的近似值,当x=mm时,(x﹣x1)2+(x﹣x2)2+…+(x﹣xn)2最小.
15. 对某条线段的长度进行了3次测量,得到3个结果(单位:mm)9.9,10.1,10.0,若用a作为这条线段长度的近似值,当10.0mm时,最小.对另一条线段的长度进行了n次测量,得到n个结果(单位:mm)x1 , x2 , …xn , 若用x作为这条线段长度的近似值,当x=mm时,(x﹣x1)2+(x﹣x2)2+…+(x﹣xn)2最小.三、综合题
-
16. 如图所示,在△ABC中,∠B=90°,AB=5厘米,BC=7厘米.点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,当B点运动到C点时停止,P点也同时停止.
 (1)、如果点P,Q分别从点A,B同时出发,那么几秒后,△PBQ的面积等于4平方厘米?(2)、如果点P,Q分别从点A,B同时出发,问第几秒时,四边形APQC的面积最小?其最小面积为多少?17. 如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2.
(1)、如果点P,Q分别从点A,B同时出发,那么几秒后,△PBQ的面积等于4平方厘米?(2)、如果点P,Q分别从点A,B同时出发,问第几秒时,四边形APQC的面积最小?其最小面积为多少?17. 如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2. (1)、写出S与x之间的函数表达式,并写出x的取值范围.(2)、当AB,BC分别为多少米时,羊圈的面积最大?最大值是多少?18. 如图,已知抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC。
(1)、写出S与x之间的函数表达式,并写出x的取值范围.(2)、当AB,BC分别为多少米时,羊圈的面积最大?最大值是多少?18. 如图,已知抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC。 (1)、求A、B、C三点的坐标;(2)、若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标。(3)、在(2)的条件下,当线段PM的长度最大时,在抛物线的对称轴上有一点Q,使得△CNQ为直角三角形,直接写出点Q的坐标。19. 已知边长为8的正方形 截去一个角后成为五边形 ,点 在线段 上,过点 作 ,垂足为点 ,过点 作 ,垂足为点 , , ,设 的长为 ,四边形 的面积记为 .
(1)、求A、B、C三点的坐标;(2)、若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标。(3)、在(2)的条件下,当线段PM的长度最大时,在抛物线的对称轴上有一点Q,使得△CNQ为直角三角形,直接写出点Q的坐标。19. 已知边长为8的正方形 截去一个角后成为五边形 ,点 在线段 上,过点 作 ,垂足为点 ,过点 作 ,垂足为点 , , ,设 的长为 ,四边形 的面积记为 . (1)、求 , 的长(分别用含 的代数式表示);(2)、求 关于 的函数关系式,并写出自变量的取值范围;(3)、求四边形 面积的最大值.
(1)、求 , 的长(分别用含 的代数式表示);(2)、求 关于 的函数关系式,并写出自变量的取值范围;(3)、求四边形 面积的最大值.