山西省吕梁市孝义市、离石区2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 下列方程是关于x的一元二次方程的是( )A、4x²+ B、2x²﹣y﹣1=0 C、ax²+2x+1=0 D、x(4x﹣2)=02. 如图,将含有30°角的三角尺ABC(∠BAC=30°),以点A为中心,顺时针方向旋转,使得点C,A,B′在同一直线上,则旋转角的大小是( )
 A、30° B、60° C、120° D、150°3. 方程x2=x的两个实数根是( )A、x1=x2=1 B、x1=1,x2=﹣1 C、x1=0,x2=1 D、x1=0,x2=﹣14. 将关于x的方程x2﹣6x+8=0配方成(x﹣3)2=p的形式,则p的值是( )A、1 B、28 C、17 D、445. 关于 的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、6. 将二次函数y=﹣2(x﹣1)2﹣2的图象先向左平移2个单位,再向上平移1个单位,则所得到的二次函数的解析式是( )A、y=﹣2(x﹣3)2﹣1 B、y=﹣2(x+1)2﹣1 C、y=﹣2(x+1)2﹣3 D、y=﹣2(x﹣3)2﹣37. 冠状病毒属的病毒是具有囊膜、基因组为线性单股正链的RNA病毒,是自然界广泛存在的一大类病毒,冠状病毒可感染多种哺乳动物、鸟类.在某次冠状病毒感染中,有3只动物被感染,后来经过两轮感染后共有363只动物被感染.若每轮感染中平均一只动物会感染x只动物,则下面所列方程正确的是( )
A、30° B、60° C、120° D、150°3. 方程x2=x的两个实数根是( )A、x1=x2=1 B、x1=1,x2=﹣1 C、x1=0,x2=1 D、x1=0,x2=﹣14. 将关于x的方程x2﹣6x+8=0配方成(x﹣3)2=p的形式,则p的值是( )A、1 B、28 C、17 D、445. 关于 的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、6. 将二次函数y=﹣2(x﹣1)2﹣2的图象先向左平移2个单位,再向上平移1个单位,则所得到的二次函数的解析式是( )A、y=﹣2(x﹣3)2﹣1 B、y=﹣2(x+1)2﹣1 C、y=﹣2(x+1)2﹣3 D、y=﹣2(x﹣3)2﹣37. 冠状病毒属的病毒是具有囊膜、基因组为线性单股正链的RNA病毒,是自然界广泛存在的一大类病毒,冠状病毒可感染多种哺乳动物、鸟类.在某次冠状病毒感染中,有3只动物被感染,后来经过两轮感染后共有363只动物被感染.若每轮感染中平均一只动物会感染x只动物,则下面所列方程正确的是( ) A、3x(x+1)=363 B、3+3x+3x²=363 C、3(1+x)²=363 D、3+3(1+x)+3(1+x)²=3638. 已知二次函数y=x2﹣4x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣4x+m=0的两个实数根是( )A、x1=1,x2=﹣1 B、x1=﹣1,x2=2 C、x1=﹣1,x2=0 D、x1=1,x2=39. 二次函数y=ax2+bx+c的图象上部分点的坐标(x,y)对应值列表如下:
A、3x(x+1)=363 B、3+3x+3x²=363 C、3(1+x)²=363 D、3+3(1+x)+3(1+x)²=3638. 已知二次函数y=x2﹣4x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣4x+m=0的两个实数根是( )A、x1=1,x2=﹣1 B、x1=﹣1,x2=2 C、x1=﹣1,x2=0 D、x1=1,x2=39. 二次函数y=ax2+bx+c的图象上部分点的坐标(x,y)对应值列表如下:x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
则关于该二次函数的图象与性质,下列说法正确的是( )
A、开口方向向上 B、当x>﹣2时,y随x增大而增大 C、函数图象与x轴没有交点 D、函数有最小值是﹣210. 在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )A、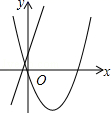 B、
B、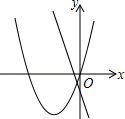 C、
C、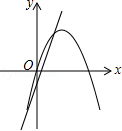 D、
D、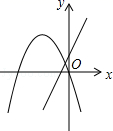
二、填空题
-
11. 如图,在⊙O中, ,半径OC与AB交于点D,若AB=8cm,OB=5cm,则CD=cm.
 12. 2022年2月4日—2月20日,北京冬奥会将隆重开幕,北京将成为世界上第一个既举办过夏季奥运会,又举办过冬季奥运会的国家.下面图片是在北京冬奥会会徽征集过程中,征集到的一幅图片,整个图片由“京字组成的雪花图案”、“beijing2022”、“奥运五环”三部分组成.对于图片中的“雪花图案”,至少旋转°能与原雪花图案重合.
12. 2022年2月4日—2月20日,北京冬奥会将隆重开幕,北京将成为世界上第一个既举办过夏季奥运会,又举办过冬季奥运会的国家.下面图片是在北京冬奥会会徽征集过程中,征集到的一幅图片,整个图片由“京字组成的雪花图案”、“beijing2022”、“奥运五环”三部分组成.对于图片中的“雪花图案”,至少旋转°能与原雪花图案重合. 13. 已知点A(4,y1)和点B(﹣1,y2)是二次函数y=﹣2(x﹣1)2+m(m为常数)的图象上两点,则y1和y2的大小关系是 .14. 2018年我国高速铁路总里程为2.9万公里,2020年我国高速铁路总里程达到3.8万公里,高速铁路已经覆盖了全国80%以上的大城市,形成以“八纵八横”主通道为骨架、区域连接线衔接、城际铁路补充的高速铁路网.若设2018年到2020年我国高速铁路总里程的平均年增长率为x,则依题意可列方程为 .
13. 已知点A(4,y1)和点B(﹣1,y2)是二次函数y=﹣2(x﹣1)2+m(m为常数)的图象上两点,则y1和y2的大小关系是 .14. 2018年我国高速铁路总里程为2.9万公里,2020年我国高速铁路总里程达到3.8万公里,高速铁路已经覆盖了全国80%以上的大城市,形成以“八纵八横”主通道为骨架、区域连接线衔接、城际铁路补充的高速铁路网.若设2018年到2020年我国高速铁路总里程的平均年增长率为x,则依题意可列方程为 . 15. 如图,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,AD的中点,若四边形EFGH是矩形,且其周长是20,则四边形ABCD的面积的最大值是 .
15. 如图,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,AD的中点,若四边形EFGH是矩形,且其周长是20,则四边形ABCD的面积的最大值是 .
三、解答题
-
16. 解方程:(1)、x(x+10)=﹣9;(2)、x(2x+3)=8x+1217. 如图,以▱ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧 和弧 是否相等,并说明理由.
 18. 在平面直角坐标系中,△ABC三个顶点的坐标分别为A(5,4),B(1,3),C(3,1),点P(a,b)是△ABC内的一点.
18. 在平面直角坐标系中,△ABC三个顶点的坐标分别为A(5,4),B(1,3),C(3,1),点P(a,b)是△ABC内的一点.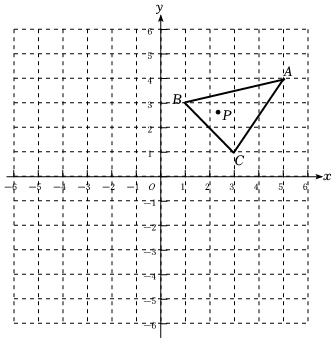 (1)、以点O为中心,把△ABC顺时针旋转90°,画出旋转后的△A1B1C1 , 并写出A1 , B1 , C1的坐标.(注:点A与A1 , B与B1 , C与C1分别是对应点)(2)、点P的对应点P1的坐标是;(3)、若以点O为中心,把△ABC逆时针旋转90°,则点P的对应点P2的坐标是 ,点P1与点P2关于对称.(填写“x轴”、“y轴”或“原点”)19. 阅读下列材料,并完成相应学习任务:
(1)、以点O为中心,把△ABC顺时针旋转90°,画出旋转后的△A1B1C1 , 并写出A1 , B1 , C1的坐标.(注:点A与A1 , B与B1 , C与C1分别是对应点)(2)、点P的对应点P1的坐标是;(3)、若以点O为中心,把△ABC逆时针旋转90°,则点P的对应点P2的坐标是 ,点P1与点P2关于对称.(填写“x轴”、“y轴”或“原点”)19. 阅读下列材料,并完成相应学习任务:一元二次方程在几何作图中的应用
如图1,在矩形ABCD中,AB=3,BC=4,求作一个矩形,使其周长和面积分别是矩形ABCD的周长和面积的2倍.

因为矩形ABCD的周长是14,面积是12,所以所求作的矩形周长是28,面积是24
若设所求作的矩形一边的长为x,则与其相邻的一边长为14﹣x,所以,得x(14﹣x)=24,解得x1=2,x2=12
当x=2时,14﹣x=12;当x=12时,14﹣x=2,所以求作的矩形相邻两边长分别是2和12
如图2,在边AB的延长线取点G,使得AG=4AB.在AD上取AE= AD,以AG和AE为邻边作出矩形AGFE,则矩形AGFE的周长和面积分别是矩形ABCD的周长和面积的2倍.
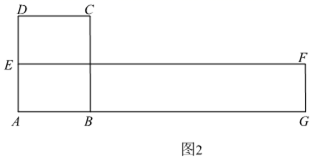
学习任务:
(1)、在作出矩形AGFE的过程中,主要体现的数学思想是___________;(填出序号即可)A、转化思想; B、数形结合思想; C、分类讨论思想; D、归纳思想(2)、是否存在一个矩形,使其周长与面积分别是矩形ABCD的周长和面积的 ?若存在,请在图1中作出符合条件的矩形;若不存在,请说明理由.20. 漪汾桥是太原市首座对称双七拱吊桥,每个桥拱呈大小相等的抛物线型,桥拱如长虹岀水,屹立于汾河之上,是太原市地标性建筑之一.如图2所示,单个桥拱在桥面上的跨度OA=60米,在水面的跨度BC=80米,桥面距水面的垂直距离OE=7米,以桥面所在水平线为x轴,OE所在直线为y轴建立平面直角坐标系. (1)、求桥拱所在抛物线的函数关系表达式;(2)、求桥拱最高点到水面的距离是多少米?21. 下面是小明解决某数学问题的过程,请认真阅读并解决相应学习任务:
(1)、求桥拱所在抛物线的函数关系表达式;(2)、求桥拱最高点到水面的距离是多少米?21. 下面是小明解决某数学问题的过程,请认真阅读并解决相应学习任务:数学问题:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:( ).现已知商品的进价为每件40元,如何定价才能使每个星期的利润达到6080元,且顾客能够得到更大的实惠?
解:设…,
根据题意,所列出方程:(20﹣x)(300+ ×40)=6080,
…
根据小明所列方程,完成下列任务:
(1)、填空:数学问题中括号处短缺的条件是 , 小明所列方程中未知数x的实际意义是 .(2)、请你重新设一个未知数,要求所设未知数与小明所列方程中未知数的意义不同,并结合所补充的条件,解决上面的数学问题.22. 问题情境:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,点E是边CD上一点,将△ADE以点A为中心,顺时针旋转90°,得到△ABF,连接EF.过点A作AG⊥EF,垂足为G.试猜想FG与GE的数量关系,并证明. (1)、独立思考:请你解决老师所提出的问题;(2)、拓展探究:智慧小组在老师所提问题的基础上,连接DG,他们认为DG平分∠ADC.请你利用图2说明,智慧小组所提出的结论是否符合题意?请说明理由;(3)、问题解决:在图2中,若AD+DE=28,则四边形AGED的面积为 . (直接写出答案即可)23. 已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是y轴右侧抛物线上一个动点.
(1)、独立思考:请你解决老师所提出的问题;(2)、拓展探究:智慧小组在老师所提问题的基础上,连接DG,他们认为DG平分∠ADC.请你利用图2说明,智慧小组所提出的结论是否符合题意?请说明理由;(3)、问题解决:在图2中,若AD+DE=28,则四边形AGED的面积为 . (直接写出答案即可)23. 已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是y轴右侧抛物线上一个动点. (1)、求出点A,B,C的坐标;(2)、如图1,当点D在第四象限时,求出△BCD面积的最大值,并求出这时点D坐标;(3)、当∠DAB=∠ABC时,求出点D的坐标.
(1)、求出点A,B,C的坐标;(2)、如图1,当点D在第四象限时,求出△BCD面积的最大值,并求出这时点D坐标;(3)、当∠DAB=∠ABC时,求出点D的坐标.