山东省泰安市岱岳区2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是( )A、sinA= B、tanA= C、tanB= D、cosB=2. 若反比例函数 经过点(2,6),则此图象也经过下列点( )A、(﹣2,6) B、(5,7) C、(4,3) D、(﹣6,2)3. 二次函数y=(x﹣1)2﹣3的顶点坐标是( )A、(1,3) B、(﹣1,3) C、(1,﹣3) D、(﹣1,﹣3)4. 下列二次函数中,其图象的对称轴为直线x=﹣2的是( )A、y=2x2﹣2 B、y=﹣2x2﹣4 C、y=x2+2x D、y= x2+2x5. 抛物线y=x2+x﹣6与x轴的交点坐标是( )A、(0,﹣6) B、(0,6) C、(3,0),(﹣2,0) D、(﹣3,0),(2,0)6. 已知正比例函数y1=kx的图象与反比例函数y2= 的图象相交于点A(2,4),则下列说法正确的是( )A、正比例函数y1与反比例函数y2都随x的增大而增大 B、两个函数图象的另一交点坐标为(2,﹣4) C、当x<﹣2或0<x<2时,y1<y2 D、反比例函数y2的解析式是y2=﹣7. 已知二次函数 的 与 的部分对应值如下表:
…
-1
0
1
3
…
…
-3
1
3
1
…
则下列判断中正确的是( )
A、抛物线开口向上 B、抛物线与 轴的交点在 轴负半轴上 C、当 时, D、方程 的正根在3与4之间8. 直线 不经过第三象限,那么 的图像大致为( )A、 B、
B、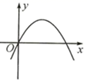 C、
C、 D、
D、 9. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,点 , .若反比例函数 经过点C,则k的值等于( )
9. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,点 , .若反比例函数 经过点C,则k的值等于( ) A、10 B、24 C、48 D、5010. 如图,在C处测得旗杆AB的顶端A的仰角为30°,向旗杆前进10米到达D处,在D处测得A的仰角为60°,则旗杆的高为( )米.
A、10 B、24 C、48 D、5010. 如图,在C处测得旗杆AB的顶端A的仰角为30°,向旗杆前进10米到达D处,在D处测得A的仰角为60°,则旗杆的高为( )米.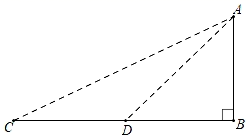 A、5 +3 B、10 C、5 D、5 +511. 函数y= 和y= 在第一象限内的图象如图,点P是y= 的图象上一动点,PC⊥x轴于点C,交y= 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA= AP.其中所有正确结论的序号是( )
A、5 +3 B、10 C、5 D、5 +511. 函数y= 和y= 在第一象限内的图象如图,点P是y= 的图象上一动点,PC⊥x轴于点C,交y= 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA= AP.其中所有正确结论的序号是( )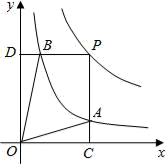 A、①②③ B、②③④ C、①③④ D、①②④12. 如图是二次函数 图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1), 是抛物线上两点,则y1>y2 , 其中说法正确的有( )
A、①②③ B、②③④ C、①③④ D、①②④12. 如图是二次函数 图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1), 是抛物线上两点,则y1>y2 , 其中说法正确的有( )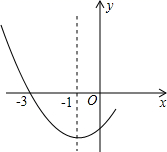 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
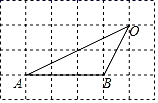
13. 函数y= 中,自变量x的取值范围是 .14. 把二次函数y=2x2﹣6x+1化成y=a(x﹣h)2+k的形式为 .15. 如图,在每个小正方形的边长为1的网格中,△ABO的顶点A、点B、点O均落在格点上,则∠AOB的正弦值为 .
 16. 如图,平行四边形ABCD的对角线AC在y轴上,原点O为AC的中点,点D在第一象限内,AD x轴,当双曲线 经过点D时,则平行四边形ABCD面积为 .
16. 如图,平行四边形ABCD的对角线AC在y轴上,原点O为AC的中点,点D在第一象限内,AD x轴,当双曲线 经过点D时,则平行四边形ABCD面积为 . 17. 如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为海里.
17. 如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为海里.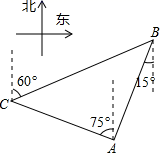 18. 如图,某隧道美化施工,横截面形状为抛物线y=﹣ x2+8(单位:米),施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,则脚手架高DE为米.
18. 如图,某隧道美化施工,横截面形状为抛物线y=﹣ x2+8(单位:米),施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,则脚手架高DE为米.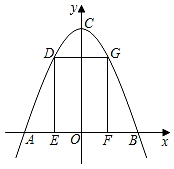
三、解答题
-
19. 计算:(1)、6tan230°﹣ sin60°﹣2tan45°;(2)、sin60°cos60°+sin45°cos45°﹣sin30°cos30°.20. 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 的一部分.请根据图中信息解答下列问题:
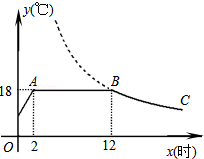 (1)、恒温系统在这天保持大棚内温度18℃的时间有多少小时?(2)、求k的值;(3)、当x=16时,大棚内的温度约为多少度?21. 王浩同学用木板制作一个带有卡槽的三角形手机架,如图1所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
(1)、恒温系统在这天保持大棚内温度18℃的时间有多少小时?(2)、求k的值;(3)、当x=16时,大棚内的温度约为多少度?21. 王浩同学用木板制作一个带有卡槽的三角形手机架,如图1所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2) 22. 如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
22. 如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m. (1)、在如图的坐标系中求抛物线的解析式;(2)、若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?23. 已知:如图,在平面直角坐标系xOy中,直线AB分别与x轴、y轴交于点B,A,与反比例函数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO= ,OB=4,OE=2.
(1)、在如图的坐标系中求抛物线的解析式;(2)、若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?23. 已知:如图,在平面直角坐标系xOy中,直线AB分别与x轴、y轴交于点B,A,与反比例函数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO= ,OB=4,OE=2.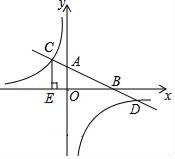 (1)、求该反比例函数的解析式;(2)、求三角形CDE的面积.24. 某药店选购了一批消毒液,进价为每瓶10元,在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间存在一次函数关系(其中10≤x≤21,且x为整数).当每瓶消毒液售价为12元时,每天销售量为90瓶;当每瓶消毒液售价为15元时,每天销售量为75瓶.(1)、求y与x之间的函数关系式;(2)、设该药店销售该消毒液每天的销售利润为w元,当每瓶消毒液售价为多少元时,药店销售该消毒液每天销售利润最大,最大利润是多少元?25. 已知抛物线y=﹣x2+2x+m.抛物线过点A(3,0),与x轴的另一个交点为C.与y轴交于点B.直线AB与这条抛物线的对称轴交于点P.
(1)、求该反比例函数的解析式;(2)、求三角形CDE的面积.24. 某药店选购了一批消毒液,进价为每瓶10元,在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间存在一次函数关系(其中10≤x≤21,且x为整数).当每瓶消毒液售价为12元时,每天销售量为90瓶;当每瓶消毒液售价为15元时,每天销售量为75瓶.(1)、求y与x之间的函数关系式;(2)、设该药店销售该消毒液每天的销售利润为w元,当每瓶消毒液售价为多少元时,药店销售该消毒液每天销售利润最大,最大利润是多少元?25. 已知抛物线y=﹣x2+2x+m.抛物线过点A(3,0),与x轴的另一个交点为C.与y轴交于点B.直线AB与这条抛物线的对称轴交于点P. (1)、求抛物线的解析式及点B、C的坐标;(2)、求直线AB的解析式和点P的坐标;(3)、在第一象限内的该抛物线有一点D,且S△ABD= S△ABC , 求点D的坐标.
(1)、求抛物线的解析式及点B、C的坐标;(2)、求直线AB的解析式和点P的坐标;(3)、在第一象限内的该抛物线有一点D,且S△ABD= S△ABC , 求点D的坐标.