山东省聊城市阳谷县2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 下列说法正确的是( )A、对应边成比例的两个五边形相似 B、对应角相等的多边形相似 C、位似可以改变图形的形状、大小和位置 D、经过复制、放大、缩小后的四边形与原图形相似2. 在平面直角坐标系中,已知点A(1,0),B(2,1),C(﹣1,2),以原点O为位似中心,位似比为2,把四边形OABC放大,则点C的对应点C的坐标为( )A、( ) B、(﹣2,4) C、(﹣2,4)或(2,﹣4) D、(﹣ ,1)或( ,1)3. 已知ABCD,CDEF,EFGH是三个相连的正方形,则△ACF与△ACG的相似比为( )
 A、1: B、1:2 C、1: D、 :4. 如图,圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成圆形阴影.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为( )
A、1: B、1:2 C、1: D、 :4. 如图,圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成圆形阴影.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为( ) A、0.36πm2 B、0.81πm2 C、1.44πm2 D、3.24πm25. 在 中, , ,则 的值是( )A、 B、 C、 D、6. 在 中, = ,若 ,则 的值为( )A、 B、 C、 D、7. 如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A、0.36πm2 B、0.81πm2 C、1.44πm2 D、3.24πm25. 在 中, , ,则 的值是( )A、 B、 C、 D、6. 在 中, = ,若 ,则 的值为( )A、 B、 C、 D、7. 如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( ) A、5m B、2 m C、4 m D、 m8. 如图,在菱形ABCD中,DE⊥AB, ,BE=2,则tan∠DBE的值是( )
A、5m B、2 m C、4 m D、 m8. 如图,在菱形ABCD中,DE⊥AB, ,BE=2,则tan∠DBE的值是( )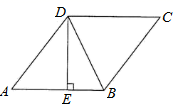 A、 B、2 C、 D、9.
A、 B、2 C、 D、9.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
 A、第①块 B、第②块 C、第③块 D、第④块10. 如图,一只花猫发现一只老鼠溜进了一个内部连通的鼠洞,鼠洞只有三个出口A,B,C,要想同时顾及这三个出口以防老鼠出洞,这只花猫最好蹲守在( )
A、第①块 B、第②块 C、第③块 D、第④块10. 如图,一只花猫发现一只老鼠溜进了一个内部连通的鼠洞,鼠洞只有三个出口A,B,C,要想同时顾及这三个出口以防老鼠出洞,这只花猫最好蹲守在( ) A、△ABC的三边高线的交点P处 B、△ABC的内角平分线的交点P处 C、△ABC的三边中线的交点P处 D、△ABC的三边垂直平分线的交点P处11. 如图,AB , BC是⊙O的两条弦,AO⊥BC , 垂足为D , 若⊙O的半径为5,BC=8,则AB的长为( )
A、△ABC的三边高线的交点P处 B、△ABC的内角平分线的交点P处 C、△ABC的三边中线的交点P处 D、△ABC的三边垂直平分线的交点P处11. 如图,AB , BC是⊙O的两条弦,AO⊥BC , 垂足为D , 若⊙O的半径为5,BC=8,则AB的长为( ) A、8 B、10 C、 D、12. 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A、8 B、10 C、 D、12. 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( ) A、45° B、50° C、60° D、120°
A、45° B、50° C、60° D、120°二、填空题
-
13. 在△ABC中,∠B=45°,cosA= , 则∠C的度数是 .14. 如图,点P是 内一点,过点P分别作直线平行于 的各边,所形成的三个小三角形 (图中阴影部分)的面积分别是1,9和49.则 的面积是 .
 15. 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD= .
15. 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD= . 16. 如图,▱ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于 .
16. 如图,▱ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于 . 17. △ABC的三边为2,3, ,设其外心为O,三条高的交点为H,则OH的长为.18. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4.点M1、N1、P1分别在AC、BC、AB上,且四边形M1CN1P1是正方形,点M2、N2、P2分别在P1N1、BN1、BP1上,且四边形M2N1N2P2是正方形,…,点Mn、Nn、Pn分别在Pn-1Nn-1、BNn-1、BPn-1上,且四边形MnNn-1NnPn是正方形,则BN2019的长度是 .
17. △ABC的三边为2,3, ,设其外心为O,三条高的交点为H,则OH的长为.18. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4.点M1、N1、P1分别在AC、BC、AB上,且四边形M1CN1P1是正方形,点M2、N2、P2分别在P1N1、BN1、BP1上,且四边形M2N1N2P2是正方形,…,点Mn、Nn、Pn分别在Pn-1Nn-1、BNn-1、BPn-1上,且四边形MnNn-1NnPn是正方形,则BN2019的长度是 .
三、解答题
-
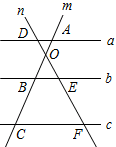
19. 如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
 20. 如图,在△ABC中,D在AC上,DE∥BC,DF∥AB.
20. 如图,在△ABC中,D在AC上,DE∥BC,DF∥AB. (1)、求证:△DFC∽△AED;(2)、若CD= AC,求S△DFC/S△AED的值.21. 在图1中,D是BC边上的点(不与点B、C重合),连结AD.
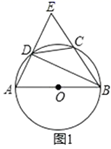
(1)、求证:△DFC∽△AED;(2)、若CD= AC,求S△DFC/S△AED的值.21. 在图1中,D是BC边上的点(不与点B、C重合),连结AD. (1)、问题引入:如图1,当点D是BC边上的中点时,求S△ABD:S△ABC=;当点D是BC边上任意一点时,求S△ABD:S△ABC=(用图中已有线段表示).(2)、探索研究:如图2,在图2中,O是线段AD上任意一点(不与点A、D重合),连接BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.22. 如图,小杰在高层楼A点处,测得多层楼CD最高点D的俯角为30°,小杰从高层楼A处乘电梯往下到达B处,又测得多层楼CD最低点C的俯角为10°,高层楼与多层楼CD之间的距离为CE,已知AB=CE=30米,求多层楼CD的高度.(结果精确到1米)(参考数据: ≈1.73,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
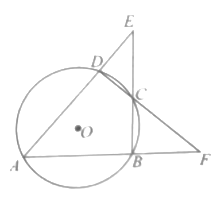
(1)、问题引入:如图1,当点D是BC边上的中点时,求S△ABD:S△ABC=;当点D是BC边上任意一点时,求S△ABD:S△ABC=(用图中已有线段表示).(2)、探索研究:如图2,在图2中,O是线段AD上任意一点(不与点A、D重合),连接BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.22. 如图,小杰在高层楼A点处,测得多层楼CD最高点D的俯角为30°,小杰从高层楼A处乘电梯往下到达B处,又测得多层楼CD最低点C的俯角为10°,高层楼与多层楼CD之间的距离为CE,已知AB=CE=30米,求多层楼CD的高度.(结果精确到1米)(参考数据: ≈1.73,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18) 23. 如图,一段河堤的斜坡BC=12m,为了加固河堤,需要将堤坝加厚竣工后,斜坡的坡度由原来1:2变成1:3.加固后斜坡AD的长是多少?
23. 如图,一段河堤的斜坡BC=12m,为了加固河堤,需要将堤坝加厚竣工后,斜坡的坡度由原来1:2变成1:3.加固后斜坡AD的长是多少? 24. 如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
24. 如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米. (1)、求圆弧所在的圆的半径r的长;(2)、当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
(1)、求圆弧所在的圆的半径r的长;(2)、当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?